cách tính đồ thị hàm số y=ax^2 Hướng dẫn FULL

Kinh Nghiệm về phương pháp tính đồ thị hàm số y=ax^2 2022

Quý khách đang tìm kiếm từ khóa phương pháp tính đồ thị hàm số y=ax^2 được Cập Nhật vào lúc : 2022-12-18 16:41:09 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.

Bài viết này toàn bộ chúng ta cùng khối mạng lưới hệ thống lại một số trong những kiến thức và kỹ năng về hàm số bậc hai ở lớp 9, đặc biệt quan trọng triệu tập vào phần Bài tập về đồ thị của hàm số bậc hai để những em nắm vững được phương pháp giải dạng toán này.

I. Hàm số bậc hai – kiến thức và kỹ năng cần nhớ

Tổng quát, hàm số bậc haiy = ax2 (a0) xác lập với mọi giá trị của xR.

1. Tính chất của hàm số bậc hai y = ax2

Nếu a>0 thì hàm số nghịch biến khi x<0 và đồng biến khi x>0.

Nếu a<0 thì hàm số đồng biến khi x<0 và nghịch biến khi x>0.

> Nhận xét:

Nếu a>0 thì y>0 với mọi x0; y=0 khi x=0. Giá trị nhỏ nhất của hàm số là y=0.

Nếu a<0 thì y<0 với mọi x0; y=0 khi x=0. Giá trị lớn số 1 của hàm số là y=0.

2. Đồ thị của hàm số y = ax2

Đồ thị của hàm số y = ax2 (a0) là một đường cong trải qua gốc tọa độ và nhận
trục Oy làm trục đối xứng. Đường cong này được gọi là một Parabol với đỉnh O.

Nếu a>0 thì đồ thị nằm phía trên trục hoành, O là yếu tố thấp nhất của đồ thị.

Nếu a<0 thì đồ thị nằm phía dưới trục hoành, O là yếu tố cao nhất của đồ thị.

3. Vị trí tương đối của đường thẳng và parabol

Cho đường thẳng (d): y=ax+b (a0) và parabol (P): y = kx2(k0)

Khi đó, để xét vị trí tương đối của đường thẳng (d) và parabol (P) ta xét phương trình:kx2= ax + b (1).

– Nếu phương trình (1) vô nghiệm thì (P) và (d) không giao nhau.

– Nếu phương trình (1) có hai nghiệm phân biệt thì (P) và (d) cắt nhau tại hai điểm phân biệt.

– Nếu phương trình (1) có nghiệm kép thì (P) và (d) tiếp xúc nhau

Một số dạng bài tập về vị trí tương đối của (d) và (P):

* Tìm số giao điểm của (d) và (P)

Khi đó: Xét phương trình kx2 = ax + b (1)

– Nếu phương trình (1) vô nghiệm thì (P) và (d) không giao nhau.

– Nếu phương trình (1) có hai nghiệm phân biệt thì (P) và (d) cắt nhau tại hai điểm phân biệt.

– Nếu phương trình (1) có nghiệm kép thì (P) và (d) tiếp xúc nhau

– Hoành độ giao điểm (hoặc tiếp điểm) của (P) và (d) đó đó là nghiệm của phương trình: kx2= ax + b

* Tìm tọa độ giao điểm của (d) và (P)

– Tọa độ giao điểm của (d) và (P) tùy từng số nghiệm của phương trình (1)

– Ta giải phương trình (1) tìm ra những giá trị của x. Thay giá trị x này vào công thức hàm số của (d) (hoặc (P)) ta tìm kiếm được y. Từ đó suy ra tọa độ giao vấn đề cần tìm.

* Hàm số chứa tham số. Tìm Đk của tham số để tọa độ giao điểm thỏa mãn nhu cầu Đk cho trước.

– Xét phương trình hoành độ giao điểm của (d) và (P) từ đó tính biệt thức delta và hệ thức Vi-et để giải bài toán với Đk cho sẵn.

II. Bài tập hàm số bậc hai có lời giải

* Bài tập 1 (Bài 54 trang 63 SGK Toán 9 Tập 2): Vẽ đồ thị của hai hàm số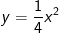và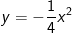trên cùng một hệ trục tọa độ.

a) Đường thẳng trải qua B(0; 4) và tuy nhiên tuy nhiên với trục Ox.Nó cắt đồ thị của hàm số 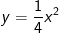tại hai điểm M và M’. Tìm hoành độ của M và M’.

b) Tìm trên đồ thị của hàm số điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có tuy nhiên tuy nhiên với Ox không? Vì sao? Tìm tung độ của N và N’ bằng hai cách:

– Ước lượng trên hình vẽ;

– Tính toán theo công thức.

* Lời giải:

a) Ta lập bảng giá trị:

– Bảng giá trị:

x

-4

-2

0

2

4

y=x2/4

4

1

0

1

4

y=-x2/4

-4

-1

0

-1

-4

Đồ thị hàm số có dạng như sau:

a) Đường thẳng qua B(0; 4) tuy nhiên tuy nhiên với Ox có dạng: y=4. Phương trình hoành độ giao điểm của đường thẳng y=4 và đồ thị hàm số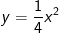là:

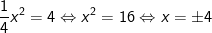
– Từ đó ta có hoành độ của M là x = 4 của M’ là x = -4.

b) Trên đồ thị hàm số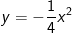ta xác lập được điểm N và N’ có cùng hoành độ với M,M’. Ta được đường thẳng M,M’. Ta được đường thẳng NN’//Ox.

Tìm tung độ của N và N’

– Ước lượng trên hình vẽ được tung độ của N là y = -4; của N’ là y = -4.

– Tính toán theo công thức:

Điểm N(4;y) thay x = 4 vào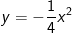nên được yN = -4.

Điểm N'(-4;y) thay x = -4 vào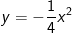nên được yN’ = -4.

Vậy tung độ của N, N’ cùng bằng -4. Ta có:N(-4;-4) ; N(4;-4).

* Bài tập 2: Trong hệ tọa độ Oxy, cho hàm số: y = f(x) = (m – 1)x2 (*)

a) Xác định m để đồ thị hàm số (*) trải qua điểm M(2;4)

b) Với m=0. Tìm tọa độ giao điểm của đồ thị hàm số (*) với đồ thị hàm số y = 2x – 3.

* Lời giải:

a) Để đồ thị hàm số y = f(x) = (m – 1)x2 trải qua điểm M(2;4) thì ta có:

4 = (m – 1).22 4 = 4m – 4 4m = 8 m = 2.

Vậy với m = 2 thì đồ thị hàm số (*) trải qua điểm (2;4). Khi đó hàm số là y = x2.

b) với m = 0, ta thay vào công thức hàm số được y = f(x) = -x2

– Tọa độ giao điểm của đồ thị hàm số y = -x2 với hàm số y = 2x – 3 là nghiệm của hệ phương trình:

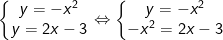
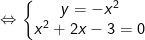
– Giải phương trình: x2 + 2x – 3 = 0 ta thấy

a + b + c = 1 + 2 + (-3) = 0 nên phương trình này còn có 2 nghiệm phân biệt x1 = 1; x2 = -3.

Với x1 = 1 y1 = -(1)2 = -1 A(1;-1)

Với x2= -3 y2= -(-3)2= -9 B(-3;-9)

Vậy với m=0 thì đồ thị hàm số y = -x2 và đồ thị hàm số y = 2x – 3 tại 2 điểm phân biệt là:A(1;-1) vàB(-3;-9).

* Bài tập 3: Co parabol (P): y = ax2 và đường thẳng (d):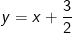

a) Xác định a để (P) cắt (d) tại điểm A có hoành độ bằng -1.

b) Tìm tọa độ giao điểm thứ hai B (B khác A) của (P) và (d).

c) Tính độ dài AB.

* Lời giải:

a) Để đường thẳng (d) trải qua A có hoành độ bằng -1 thì ta thay x = -1 vào công thức hàm số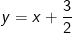được: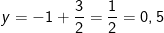

Vậy tọa độ điểm A là (-1;0,5).

Parabol (P) trải qua A nên tọa độ của A phải thỏa hàm số y = ax2. Ta thay x = -1; y = 0,5 vào hàm số y = ax2 được:

0,5 = a.(-1)2 a = 0,5. Khi đó parabol (P) là: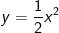

b) Xét phương trình hoành độ giao điểm của (P) và (d):

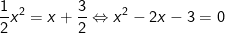
Để ý a – b + c = 1 – (-2) – 3 = 0 nên ta thấy phương trình có 2 nghiệm x1 = -1 và x2 = 3.

Với x2 = 3 y2 = 3 + 3/2 = 9/2 = 4,5.

Tọa độ điểm B là (3;4,5).

c) Ta có, chiều dài AB vận dụng công thức

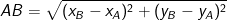
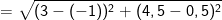
Vậy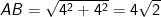

* Bài tập 4: Trong hệ tọa độ Oxy, cho parabol (P):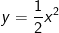và đường thẳng (d):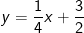. Gọi M(x1;y1) và N(x2;y2) là giao điểm của (P) và (d). Hãy tính giá trị biểu thức.

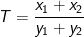* Lời giải:

– Ta có phương trình hoành độ giao điểm của (P) và (d) là:

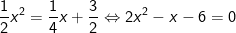
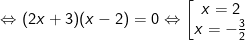
Với x1 = 2 y1 = 2 M(2;2)

Với x2 =-3/2 y2 = 9/8 N(-3/2;9/8)

Vậy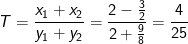

* Bài tập 5:Cho Parabol (P) : y = x2 và đường thẳng (d) : y = (2m – 1)x – m + 2 (m là tham số)

a) Chứng minh rằng với mọi m đường thẳng d luôn cắt P) tại hai điểm phân biệt.

b) Tìm những giá trị của m để đường thẳng d luôn cắt P) tại hai điểm phân biệt M(x1;y1) và N(x2;y2) thỏa x1y1 + x2y2 = 0.

* Bài tập 6:Cho parabol (P) : y = x2 và đường thẳng (d) : y = 2mx – 4m (với m là tham số)

a) Tìm tọa độ giao điểm của (d) và (P) khi m=-1/2

b) Tìm toàn bộ những giá trị của m để đường thẳng (d) cắt (P) tại hai điểm phân biệt có
hoành độ x1; x2thỏa mãn |x1| + |x2| = 3.

* Bài tập 7: Cho parabol (P):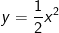và đường thẳng (d): ax + y = 1.

a) Chứng minh rằng (P) và (d) luôn cắt nhau tại hai điểm phân biệt A, B.

b) Xác định a để AB độ dài ngắn nhất và tính độ dài ngắn nhất này.

* Bài tập 8: Cho parabol (P):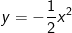và đường thẳng (d): y = mx + n. Xác định m, n để đường thẳng (d) tuy nhiên tuy nhiên với đường thẳng y = -2x + 5 và có duy nhất một điểm chung với (P).

Reply

0

0

Chia sẻ

Share Link Cập nhật phương pháp tính đồ thị hàm số y=ax^2 miễn phí

Bạn vừa tìm hiểu thêm tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Video phương pháp tính đồ thị hàm số y=ax^2 tiên tiến và phát triển nhất và ShareLink Tải phương pháp tính đồ thị hàm số y=ax^2 Free.

Thảo Luận vướng mắc về phương pháp tính đồ thị hàm số y=ax^2

Nếu sau khi đọc nội dung bài viết phương pháp tính đồ thị hàm số y=ax^2 vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Admin lý giải và hướng dẫn lại nha

#cách #tính #đồ #thị #hàm #số #yax2

Related posts: