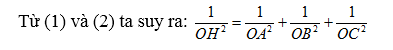Có bảo nhiêu cách chứng minh đường thẳng vuông góc với mặt phẳng Hướng dẫn FULL

byỞ Đâu •December 05, 2021

0

Mẹo về Có bảo nhiêu cách chứng tỏ đường thẳng vuông góc với mặt phẳng Chi Tiết

Bạn đang tìm kiếm từ khóa Có bảo nhiêu cách chứng tỏ đường thẳng vuông góc với mặt phẳng được Cập Nhật vào lúc : 2022-12-05 22:20:06 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha.

Đường thẳng vuông góc với mặt phẳng

A. CÁC KIẾN THỨC CẦN NHỚ

I. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

Đường thẳng d được gọi là vuông góc với mặt phẳng (α) nếu d vuông góc với mọi đường thẳng nằm trong (α).

Nội dung chính

Đường thẳng vuông góc với mặt phẳng

A. CÁC KIẾN THỨC CẦN NHỚ

B. DẠNG TOÁN CƠ BẢN

C. CÂU HỎI VÀ BÀI TẬP

Khi đó ta còn nói (α) vuông góc với d và kí hiệu d $perp$ (α) hoặc (α) $perp$ d.

II. ĐIỂU KIỆN ĐỂ ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

Nếu đường thẳng d vuông góc với hai tuyến phố thẳng cắt nhau nằm trong mặt phẳng (α) thì d vuông góc với (α).

III. TÍNH CHẤT

1. Có duy nhất một mặt phẳng trải qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

2.Có duy nhất một đường thẳng trải qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

IV.SỰ LIÊN QUAN GIỮA QUAN HỆ VUÔNG GÓC VÀ QUAN HỆ SONG SONG

1.a) Cho hai tuyến phố thẳng tuy nhiên tuy nhiên. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì tuy nhiên tuy nhiên với nhau.

2.a) Cho hai mặt phẳng tuy nhiên tuy nhiên. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.

b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì tuy nhiên tuy nhiên với nhau.

3.a) Cho đường thẳng a và mặt phẳng (α) tuy nhiên tuy nhiên với nhau. Đường thẳng nào vuông góc với (α) thì cũng vuông góc với

b) Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng khác thì chúng tuy nhiên tuy nhiên với nhau.

V. PHÉP CHIẾU VUÔNG GÓC VÀ ĐỊNH LÍ BA ĐƯỜNG VUÔNG GÓC

1.Định nghĩa. Cho đường thẳng d vuông góc với mặt phẳng (α). Phép chiếu tuy nhiên tuy nhiên theo phương d lên mặt phẳng (α) được gọi là phép chiếu vuông góc lên mặt phẳng (α).

2. Định lí ba đường vuông góc. Cho đường thẳng a nằm trong mặt phẳng (α) và b là đường thẳng không thuộc (α) đồng thời không vuông góc với (α). Gọi b là hình chiếu vuông góc của b trên (α). Khi đó a vuông góc với b khi và chỉ khi a vuông góc với b

3. Góc giữa đường thẳng và mặt phẳng

Cho đường thẳng d và mặt phẳng (α). Ta có định nghĩa :

Nếu đường thẳng d vuông góc với mặt phẳng (α) thì ta nói rằng góc giữa đường thẳng d và mặt phẳng (α) bằng 90°.

Nếu đường thẳng d không vuông góc với mặt phẳng (α) thì góc giữa d và hình chiếu d của nó trên (à) được gọi là góc giữa đường thẳng d và mặt phẳng (α).

Lưu ý rằng góc giữa đường thẳng và mặt phẳng không vượt quá 90°.

B. DẠNG TOÁN CƠ BẢN

Vấn đề 1

Chứng minh đưòng thẳng vuông góc với mặt phẳng

1. Phương pháp giải

Muốn chứng tỏ đường thẳng a vuông góc với mặt phẳng (α) người ta thường dùng một trong hai cách sau này :

Chứng minh đường thẳng a vuông góc với hai tuyến phố thẳng cắt nhau nằmtrong (α).

Chứng minh đường thẳng a tuy nhiên tuy nhiên với đường thẳng b mà b vuông gócvới (α).

2. Ví dụ

Ví dụ 1. Hình chóp S.ABCD có đáy là hình vuông vắn ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Gọi H, I vầK lần lượt là hình chiếu vuông góc của điểm A trên những cạnh SB, SC và SD.

a) Chứng minh BC $perp$ (SAB), CD $perp$ (SAD) và BD $perp$ (SAC).

b) Chứng minh SC $perp$ (ẠHK) và điểm I thuộc (AHK).

c) Chứng minh HK $perp$ (SAC), từ đó suy ra HK $perp$ AI.

Giải

a) BC $perp$ AB vì đáy ABCD là hình vuông vắn (h.3.24)

BC $perp$ SA vì SA $perp$ (ABCD) và BC thuộc (ABCD).

Do đó BC $perp$ (SAB) vì BC vuông góc với hai tuyến phố thẳng cắt nhau trong (SAB).

Lập luận tương tự ta có CD $perp$ AD và CD $perp$ SA nên CD $perp$ (SAD).

Ta có BD $perp$ AC vì đáy ABCD là hình vuông vắn và BD $perp$ SA nên BD $perp$ (SAC).

b) BC $perp$ (SAB) mà AH (,SAB) nên BC $perp$ AHvà theo giả thiết SB $perp$ AH ta suy ra AH $perp$ (SBC).

Vì SC (SBC) nên AH $perp$ SC.

Lập luận tương tự ta chứng tỏ được AK $perp$ SC. Hai đường thẳng AH, AK cắt nhau và cùng vuông góc với SC nên chúng nằm trong mặt phẳng trải qua điểm A và vuông góc với SC. Vậy SC $perp$ (AHK). Ta có AI (.AHK) vì nó trải qua điểm A và cùng vuông góc với SC.

Hai tam giác vuông SAB và SAD bằng nhau vì chúng có cạnh SA chung và AB AD (c.g.c). Do đó SB = SD, SH = SK nên HK // BD.

Vì BD $perp$ (SAC) nên HK (SAC) và do AI c= (SAC) nên HK $perp$ AI.

Ví dụ 2. Hình chóp S.ABCD có đáy là hình thoi ABCD tâm O và có SA = SC, SB = SD.

a) Chứng minh so vuông góc với mặt phẳng (ABCD).

b) Gọi I, K lần lượt là trung điểm của những cạnh BA, BC.

Chứng minh rằng IK $perp$ (SBD) và IK $perp$ SD.

Giải

a) O là tâm hình thoi ABCD nên O làtrung điểm của đoạn AC (h.3.25). Tamgiác SAC có SA = SC nên so $perp$ ÁC.Chứng minh tương tự ta có SO $perp$ BD. Từđó ta suy ra SO $perp$ (ABCD).

b) Vì đáy ABCD là hình thoi nên AC $perp$ BD

Mặt khác ta có AC $perp$ SO. Do đó AC $perp$ (SBD). Ta có IK là đường trung bình của tam giác BAC nên IK // AC mà AC $perp$ (SBD) nên IK $perp$ (SBD).

Ta lại sở hữu SD nằm trong mặt phẳng (SBD) nên IK $perp$ SD.

Vấn đề 2

Chứng minh hai tuyến phố thẳng vuông góc với nhau bằng phương pháp chứng tỏ đường thẳng nàỵ vuông góc với mặt phẳng chứa đường thẳng kia

1. Phương pháp giải

Muốn chứng tỏ đường thẳng a vuông góc với đường thẳng b, ta tìm mặt phẳng (β) chứa đường thẳng b sao cho việc chứng tỏ a $perp$ (β) dễ thực thi.

Sử dụng định lí ba đường vuông góc.

2. Ví dụ

Ví dụ 1. Cho tứ diện đều ABCD. Chứng minh những cặp cạnh trái chiều của tứ diện này vuông góc với nhau từng đôi một.

Giải

Đường thẳng vuông góc với mặt phẳng

Giả sử ta cần chứng tỏ AB $perp$ CD.

Gọi I là trung điểm của cạnh AB (h3.26). Ta có :

Do đó AB $perp$ CD vì CD nằm trong mặt phẳng (CID).

Bằng lập luận tương tự ta chứng tỏ được BC $perp$ AD và AC $perp$ BD.

Ví dụ 2. Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Chứng minh :

a) OA $perp$ BC, OB $perp$ CA và OC $perp$ AB

b) H là trực tâm của tam giác ABC;

Giải

OA $perp$ (OBC) OA $perp$ BC (h.3.27).

Tương tự ta chứng tỏ

OB $perp$ (OCA) OB $perp$ CA

OC $perp$ (OAB) OC $perp$ AB.
b) Vì OH $perp$ (ABC) nên OH $perp$ BC và OA $perp$ BC

BC $perp$ (OAH) BC $perp$ AH. (1)

Chứng minh tương tự ta có AC $perp$ (OBH) AC $perp$ BH. (2)
Từ (1) và (2) ta suy ra H là trực tâm của tam giác ABC.

Gọi K là giao điểm của AH và Trong tam giác AOK vuông tại O, ta có OH là đường cao. Dựa vào hệ thức lượng trong tam giác vuông của hình học phẳng ta có :

Vì BC vuông góc vói mặt phẳng (OAH) nên BC _L OK. Do đố trong tam giác OBC vuông tại o với đường cao OK ta có :

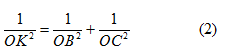
Ví dụ 3. Hình chóp S.ABCD có đáy là hình chữ nhật ABCD và có cạnh bên SA vuông góc với mặt phẳng đáy. Chứng minh những mặt bên của hình chóp đã cho là những tam giác vuông.

Giải

SA $perp$ AB và SA $perp$ AD (h.3.28).

Vậy những tam giác SAB và SAD là những tam giác vuông tại A.

Đường thẳng vuông góc với mặt phẳng

Vậy tam giác SDC vuông tại D và tam giác SBC vuông tại B.

Chú thích. Muốn chứng tỏ tam giác SDC vuông tại D ta hoàn toàn có thể vận dụng định lí ba đường vuông góc và lập luận như sau

Đường thẳng SD có hình chiếu vuông góc trên mặt phẳng (ABCD) là AD. Theo định lí ba đường vuông góc vì CD $perp$ AD nên CD $perp$ SD và ta có tam giác SDC vuông tại D.

Tương tự, ta chứng tỏ được CB $perp$ SB và ta có tam giác SBC vuông tại B.

C. CÂU HỎI VÀ BÀI TẬP

3.16.Một đoạn thẳng AB không vuông góc với mặt phẳng (α) cắt mặt phẳng này tại trung điểm O của đoạn thẳng đó. Các đường thẳng vuông góc với (α) qua A và B lần lượt cắt mặt phẳng (α) tại A và B.

Chứng minh ba điểm A, O, B thẳng hàng và AA = BB.

Xem đáp án tại đây.

3.17.Cho tam giác Gọi (α) là mặt phẳng vuông góc với đường thẳng CA tại A và (β) là mặt phẳng vuông góc với đường thẳng CB tại B. Chứng minh rằng hai mặt phẳng (α) và (β) cắt nhau và giao tuyến d của chúng vuông góc với mặt phẳng (ABC).

Xem đáp án tại đây.

3.18.Cho hình lăng trụ tam giác ABC. Gọi H là trực tâm của tam giác ABC và biết rằng AH vuông góc với mặt phẳng (ABC). Chứng minh rằng :

a )AA $perp$ BC và lAA $perp$ BC.

b) Gọi MM là giao tuyến của mặt phẳng (ẠHA) với mặt bên BCCB trong số đó M BC và M BC. Chứng minh rằng tứ giác BCCB là hình chữ nhật và MM là đường cao của hình chữ nhật đó.

Xem đáp án tại đây.

3.19.Hình chóp tam giác ABC có đáy ABC là tam giác vuông tại A và có canh bên SA vuông góc với mặt phẳng đáy là (ABC). Gọi D là yếu tố đối xứng của điểm B qua trung điểm o của cạnh AC. Chứng minh rằng CD $perp$ CA và CD $perp$ (SCA).

Xem đáp án tại đây.

3.20.Hai tam giác cân ABC và DBC nằm trong hai mặt phẳng rất khác nhau có chung cạnh đáy BC tạo ra tứ diện Gọi I là trung điểm của cạnh BC.

a) Chứng minh BC $perp$ AD

b) Gọi AH là đường cao của tam giác ADI

Chứng minh rằng AH vuông góc vói mặt phẳng (BCD).

Xem đáp án tại đây.

3.21.Chứng minh rằng tập hợp những điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn (C) ngoại tiếp tam giác ABC đó.

Xem đáp án tại đây.

Chia Sẻ Link Down Có bảo nhiêu cách chứng tỏ đường thẳng vuông góc với mặt phẳng miễn phí

Bạn vừa Read tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Video Có bảo nhiêu cách chứng tỏ đường thẳng vuông góc với mặt phẳng tiên tiến và phát triển nhất và Chia SẻLink Download Có bảo nhiêu cách chứng tỏ đường thẳng vuông góc với mặt phẳng miễn phí.

Hỏi đáp vướng mắc về Có bảo nhiêu cách chứng tỏ đường thẳng vuông góc với mặt phẳng

Nếu sau khi đọc nội dung bài viết Có bảo nhiêu cách chứng tỏ đường thẳng vuông góc với mặt phẳng vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha

#Có #bảo #nhiêu #cách #chứng #minh #đường #thẳng #vuông #góc #với #mặt #phẳng

Related posts: