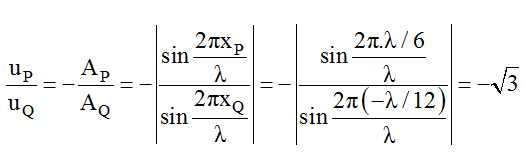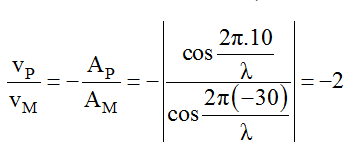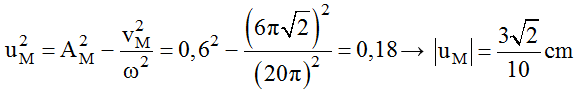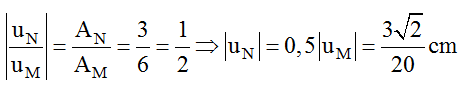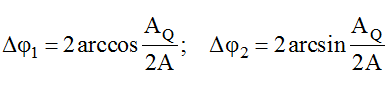Kinh Nghiệm về Tỉ số giữa khoảng chừng cách lớn số 1 và nhỏ nhất 2022
Quý khách đang tìm kiếm từ khóa Tỉ số giữa khoảng chừng cách lớn số 1 và nhỏ nhất được Cập Nhật vào lúc : 2022-12-29 13:36:10 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Cách giải Bài tập về phương trình sóng dừng hay, rõ ràng
Trang trước
Trang sau
Quảng cáo
1. Các biểu thức sóng dừng và biên độ sóng tại những điểm
a) Nếu chọn gốc tọa độ O trùng với nút sóng, gốc thời hạn là lúc những thành phần sóng tại bó gần O nhất đang trải qua vị trí cân đối theo chiều dương.
+ Phương trình xấp xỉ tổng hợp tại M là:
uM = 2a sin (2πxn/ λ)cos (ωt – π/2)
Biên độ xấp xỉ tổng hợp tại M là: AM = 2a|sin (2πxn/λ )|
(Với xn là khoảng chừng cách từ điểm M cần xét đến nút chọn làm gốc).
Lưu ý: Công thức tính biên độ trên cũng đúng cho trường hợp xn là khoảng chừng cách từ M tới nút bất kỳ.
+ Vận tốc xấp xỉ của thành phần tại M là: vM = uM (t) = 2aω sin (2πxn/λ)cos(ωt)
+ Hệ số góc tiếp tuyến tại điểm M trên dây: k = tanα = ux = 2a.2π /λ . cos (2πxn/λ) cos (ωt – π/2)
b) Nếu chọn gốc tọa độ O trùng với bụng sóng, gốc thời hạn là lúc thành phần bụng sóng tại O đang trải qua vị trí cân đối theo chiều dương.
+ Phương trình xấp xỉ tổng hợp tại M là:
uM = 2a cos (2πxb/ λ)cos (ωt – π/2)
+ Biên độ xấp xỉ tổng hợp tại M là: AM = 2a|cos (2πxb/λ )|
(Với xb là khoảng chừng cách từ điểm M cần xét đến bụng chọn làm gốc).
Lưu ý: Công thức tính biên độ trên cũng đúng cho trường hợp xb là khoảng chừng cách từ M tới nút bất kỳ.
+ Vận tốc xấp xỉ của thành phần tại M là: vM = uM (t) = 2aω cos (2πxb/λ)cos(ωt)
+ Hệ số góc tiếp tuyến tại điểm M trên dây: k = tanα = u’x = -2a.2π /λ . sin (2πxb/λ) cos (ωt – π/2)
Ví dụ 1: Một sóng dừng trên một sợi dây được mô tả bởi phương trình: u = 4 cos (πx/4 + π/2) cos (20πt – π/2)cm. Trong số đó x đo bằng cm và t đo bằng giây. Tốc độ truyền sóng dọc theo dây là:
A. 80 cm/s. B. 40 cm/s. C. 60 cm/s. D. 20 cm/s.
Hướng dẫn giải:
Chọn A.
Từ phương trình sóng u = 4 cos (πx/4 + π/2) cos (20πt – π/2)
2πx/ λ = πx/4 => λ = 8cm
Tần số sóng: f = 10Hz.
Tốc độ truyền sóng dọc theo dây là: v = λ.f = 80cm/s
Ví dụ 2: Một sóng dừng trên một sợi dây có dạng u = 2sin(πx/4)cos(20πt + π/2) (cm), trong số đó u là li độ tại thời gian t của một thành phần M trên dây mà vị trí cân đối của nó cách gốc tọa độ O một khoảng chừng x (x đo bằng cm, t đo bằng giây). Vận tốc xấp xỉ và thông số góc của tiếp tuyến của thành phần trên dây có tọa độ 1cm tại thời gian t = 1/80s lần lượt là:
A. -6 cm/s và π/4. B. -5 cm/s và -π/4.
C. -20π cm/s và -π/4. D. -30π cm/s và π/4.
Quảng cáo
Hướng dẫn giải:
Chọn C.
Vận tốc xấp xỉ và thông số góc của tiếp tuyến của thành phần trên dây được xác lập bằng biểu thức sau:
+ vdđ = u(t) = -40πsin(πx/4)cos(20πt + π/2)
+ k = tanα = u’x = 2π/4.cosπx/4 cos (20πt + π/2)
Thay x = 1cm, t = 1/80s vào ta được: vdđ = -20π cm/s; tanα = -π/4
Ví dụ 3: Sóng dừng trên dây OP = 120cm, 2 đầu cố định và thắt chặt. Ta thấy trên dây có 4 bó và biên độ xấp xỉ của bụng là 2cm. Tính biên độ xấp xỉ tại điểm M cách O là 65 cm.
A. 0,5 cm B. 1 cm. C. 0,75 cm. D. 0,9cm
Hướng dẫn giải:
Chọn B.
Dây OP có 2 đầu cố định và thắt chặt, trên dây có 4 bó nên OP = 4λ/2 λ = 60cm.
Biên độ xấp xỉ tại điểm M: AM = 2a|sin(2πxn/λ) = 2|sin(2π.65/60)| = 1cm
Ví dụ 4: Một sóng dừng trên sợi dây đàn hồi với bước sóng λ. N là yếu tố không xấp xỉ trên dây, hai điểm P và Q. ở hai bên N và có vị trí cân đối phương pháp N những khoảng chừng PN = λ/6; QN = λ/12. Tỉ số li độ của P và Q. tại thời gian P, Q. không trải qua vị trí cân đối là:
A. 1. B. 2 C. -3 D. 22
Hướng dẫn giải:
Chọn C.
N không xấp xỉ nên N là nút, ta chọn N làm gốc, khi đó: xP = λ/6, xQ = – λ/12 (P và Q. nằm ở vị trí hai bó liền kề).
Tỉ số li độ của P và Q. tại thời gian P, Q. không trải qua vị trí cân đối là:
Ví dụ 5: Một sóng dừng trên sợi dây đàn hồi với bước sóng λ = 60cm. Ba điểm theo thứ tự M, N, P trên dây (MN = 3NP = 30cm) trong số đó N là yếu tố bụng. Khi vận tốc xấp xỉ tại P là 3 cm/s thì vận tốc xấp xỉ tại M là:
A. 33 cm/s B. 22 cm/s C. -23 cm/s D. -22 cm/s.
Hướng dẫn giải:
Chọn C.
Chọn bụng N làm gốc, ta có: xM = -30cm; xP = 10cm (M và P nằm ở vị trí hai bó liền kề)
=> vM = -2vP = -23 cm/s
d) Các điểm (không phải bụng, nút) liên tục có cùng biên độ.
* Hai điểm (không phải bụng, nút) liên tục có cùng biên độ.
Hai điểm này còn có cùng biên độ A1 thì hoặc hai điểm này nằm hai bên nút hoặc nằm hai bên bụng.
Nếu chúng nằm hai bên nút thì chúng sẽ nằm trên hai bó liền kề (xấp xỉ ngược pha) và những điểm nằm trong tâm chúng sẽ có được biên độ nhỏ hơn A1.
Ta có: A1 = 2a|sin2πxn/λ| = 2a sin πΔd/λ (d là khoảng chừng cách của hai điểm đang xét)
Ví dụ 6: Một sợi dây đàn hồi có sóng dừng, biên độ tại bụng sóng là 2A (cm). M là một điểm nằm trên dây có phương trình uM = A.cos(10πt + π/3) cm, điểm N có phương trình uN = A.cos(10πt – 2π/3) cm, vận tốc truyền sóng trên dây là một trong,2 m/s. Khoảng cách MN nhỏ nhất là:
A. 0,02 m. B. 0,05 m. C. 0,04 m. D. 0,07m
Quảng cáo
Hướng dẫn giải:
Bước sóng: λ = v/f = 1,2/5 = 0,24m = 24cm.
Từ phương trình xấp xỉ của hai điểm m và n ta thấy chúng xấp xỉ cùng biên độ nhưng ngược pha nhau.
Hai điểm M, N gần nhau nhất thỏa mãn nhu cầu trạng thái xấp xỉ trên khi chúng nằm đối xúng nhau qua nút.
Ta có AM = AN = A = 2A|sin 2πxn/λ| = 2a sin πΔd/λ =>Δd = λ/6 = 0,04m
* Ba điểm (không phải bụng, nút) liên tục có cùng biên độ.
Giả sử 3 điểm liên tục có cùng biên độ thì trong số đó phải có hai điểm (ví dụ M, N) cùng nằm trên cùng một bó (xấp xỉ cùng pha) và một điểm còn sót lại nằm trên bó liền kề (xấp xỉ ngược pha với hai điểm M, N). Do vậy ta có: λ = 2(MN + NP).
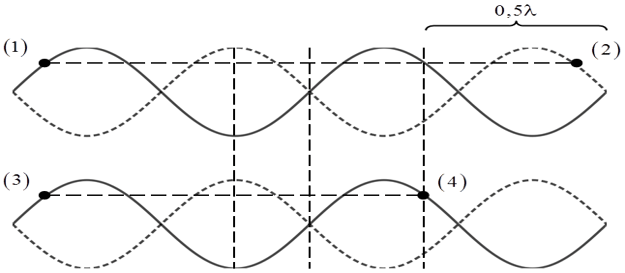
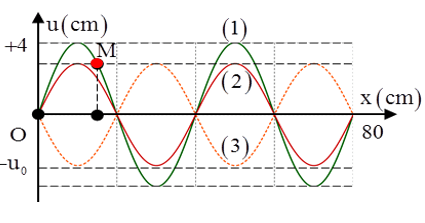
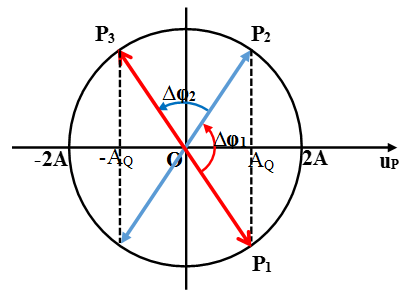
Ví dụ 7: (Quốc gia 2022) Một sợi dây căng ngang với hai đầu cố định và thắt chặt, đang sẵn có sóng dừng. Biết khoảng chừng cách xa nhất giữa hai thành phần dây xấp xỉ với cùng biên độ 5 mm là 80 cm, còn khoảng chừng cách xa nhất giữa hai thành phần dây xấp xỉ cùng pha với cùng biên độ 5 mm là 65 cm. Tỉ số giữa vận tốc cực lớn của một thành phần dây tại bụng sóng và vận tốc truyền sóng trên dây là
A. 0,21. B. 0,41. C. 0,14. D. 0,12.
Hướng dẫn giải:
Chọn D.
Ta để ý đến giả thuyết của bài toán, hai điểm xấp xỉ cùng biên độ 5 mm nhưng cùng pha nhau hai điểm này đối xứng qua một bụng.
Hai điểm khác cũng xấp xỉ với biên độ đúng bằng 5 mm nhưng lại cách xa nhau nhất mà không cùng pha vậy hai điểm này phải ngược pha nhau.
Từ hình vẽ, (1) và (2) là hai điểm xấp xỉ với cùng biên độ và cách xa nhau nhất. (3) và (4) là hai điểm xấp xỉ cùng biên độ và cùng pha, cũng cách xa nhau nhất.
Ta thuận tiện và đơn thuần và giản dị xác lập được: λ/2 = 80 – 65 = 15 => λ = 30 cm
Biên độ của những điểm (3), (4) cách bụng một đoạn d: 5 = a|cos 2πd/λ|
Thay d = 65/2 cm vào ta tìm kiếm được a = 10/3 mm
Ta có tỉ số δ = ωa/v = 2πa/λ = 0,12
* Các điểm có cùng biên độ nằm cách đều nhau.
– Các điểm bụng có cùng biên độ Amax = 2a nằm cách đều nhau những khoảng chừng d = λ/2.
– Những điểm cách đều nhau liên tục (không kể bụng và nút) có cùng biên độ xấp xỉ sẽ cách nhau 1 khoảng chừng nhỏ nhất là /4 và cùng biên độ a2 .
Ví dụ 8: Trên sợi dây đàn hồi mang sóng dừng có 3 điểm M, N, P là 3 điểm liên tục nhau có cùng biên độ A1, xấp xỉ tại N cùng pha với xấp xỉ tại M. Biết MN = 2NP = 20cm. Cứ sau khoảng chừng thời hạn ngắn nhất là 0,04s sợi dây có dạng một đoạn thẳng và biên độ tại bụng là 10cm. Tính A1 và vận tốc truyền sóng.
A. 53 cm và 60 m/s. B. 5cm và 75 cm/s.
C. 52 cm và 50 cm/s. D. 42 cm và 65 cm/s
Hướng dẫn giải:
Chọn B.
Khoảng thời hạn ngắn nhất sợi dây có dạng một đoạn thẳng là T/2 = 0,04s T = 0,08s.
Ta có: λ = (MN + NP).2 = 60cm v = λ/T = 75 cm/s.
Dao động tại N cùng pha với xấp xỉ tại M và có cùng biên độ nên 2 điểm cùng cách bụng sớm nhất một đoạn d = MN/2 = 10cm.
=> A1 = 2acos 2πd/λ = 10. cos2π10/60 = 5 cm
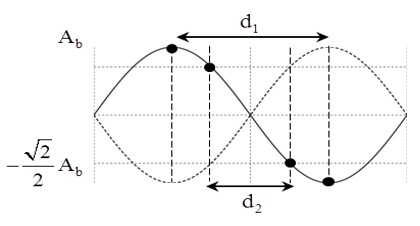
Ví dụ 9: Một sợi dây đàn hồi có sóng dừng. Trên dây có những điểm xấp xỉ với cùng biên độ A1 có vị trí cân đối liên tục cách đều nhau một đoạn d1 và những điểm xấp xỉ với cùng biên độ A2 có vị trí cân đối liên tục cách đều nhau một đoạn d2. Biết A1 > A2 > 0. Biểu thức nào sau này là đúng ?
A. d1 = 0,5d2. B. d1 = 4d2. C. d1 = 0,25d2. D. d1 = 2d2.
Hướng dẫn giải:
Chọn B.
+ Trong hiện tượng kỳ lạ sóng dừng trên dây, những điểm xấp xỉ cùng biên độ liên tục cách đều nhau chỉ hoàn toàn có thể là những điểm bụng (biên độ A1 = 2a) hoặc những điểm xấp xỉ với biên độ a2 = Ab2/2 .
Những điểm cách đều nhau liên tục (không kể bụng và nút) có cùng biên độ xấp xỉ sẽ cách nhau 1 khoảng chừng nhỏ nhất là λ/4.
Do vậy d1 = λ/2; d2 = λ/4 d1 = 2d2.
2. Xác định trạng thái, khoảng chừng thời hạn xấp xỉ điều hòa của những thành phần trong sóng dừng.
a) Li độ, vận tốc và tần suất tại những thời gian rất khác nhau.
* Ta chọn gốc tọa độ trùng với nút và gốc thời hạn hợp lý để xác lập biểu thức sóng dừng.
Ví dụ nếu lọc gốc tọa độ O trùng với nút sóng, gốc thời hạn là lúc những thành phần sóng tại bó gần O nhất đang ở biên dương (khi đó dây phồng to nhât).
Phương trình xấp xỉ tổng hợp tại M là:
uM = 2a sin(2πxn/λ)cos (ωt)
Suy ra phương trình li độ, vận tốc và tần suất cho từng điểm rõ ràng trên sợi dây. Từ đó ta xác lập được những đại lượng mà bài toán yêu cầu.
* Ta hoàn toàn có thể xác lập trạng thái xấp xỉ của những thành phần sóng bằng phương pháp sử dụng vòng tròn lượng giác như trong xấp xỉ điều hòa với lưu ý là biên độ tại mỗi điểm đang xét tùy từng vị trí của thành phần đó trên dây.
Biên độ những điểm được xác lập như phần trên.
Trong sóng dừng những điểm xấp xỉ chỉ có hai trường hợp xẩy ra:
– xấp xỉ đồng pha (những điểm nằm trên cùng một bó hoặc ở những bó cùng số chẵn hoặc cùng số lẻ).
– xấp xỉ ngược pha (những điểm nằm ở vị trí một bó số chẵn ngược pha với những điểm nằm ở vị trí bó số lẻ).
Ví dụ 1: Trên một dây đàn hồi đang sẵn có sóng dừng ổn định với mức chừng cách giữa hai nút sóng liên tục là 6cm, thành phần sóng xấp xỉ với tần số 5 Hz và biên độ lớn số 1 là 3cm. Gọi N là vị trí của một nút sóng; C, D là hai thành phần trên dây ở hai bên của N và có vị trí cân đối phương pháp N lần lượt là 10,5 cm và 7 cm. Tại thời gian t1, thành phần C có li độ 1,5 cm và đang khuynh hướng về vị trí biên. Vào thời gian t2 = t1 + 235/120 s, thành phần D có li độ là:
A. -0,75 cm. B. 1,50 cm. C. -1,50 cm. D. 0,75 cm
Hướng dẫn giải:
Chọn D.
Giải theo phương trình sóng dừng.
Bước sóng: λ = 6.2 = 12 cm.
Ta chọn gốc tọa độ O trùng với nút N, gốc thời hạn là lúc những thành phần sóng tại bó bên phải gần O nhất đang ở biên dương (khi đó dây phồng to nhât).
Biểu thức sóng dừng: u = 2a sin(2πxn/λ)cos (ωt) (cm)
Giả sử C bên trái N, D bên phải N, suy ra xC = -10,5cm; xD = 7cm.
Ta có:
Tại thời gian t1, uC = 1,5 cm và đang hướng ra phía biên (vC > 0).
Suy ra 10 πt1 = -π/4 + 2kπ (k Z)
Tại thời gian t2 = t1 + 235/120 s, thành phần D có li độ là:
uD = -1,5cos.10π(t1 + 235/120) = -1,5 cos.(10πt1 + 235π/12) (cm) = 0,75 cm
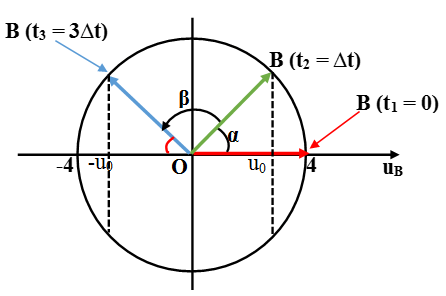
Ví dụ 2: Sóng dừng trên một sợi dây đàn hồi OB mô tả như hình dưới. Điểm O trùng với gốc tọa độ trục tung. Lúc t = 0 hình ảnh của sợi dây là (1), sau thời hạn nhỏ nhất t và 3t Tính từ lúc lúc t = 0 thì hình ảnh của sợi dây lần lượt là (2) và (3). Tốc độ truyền sóng là 20 m/s và biên độ của bụng sóng là 4 cm. Sau thời hạn 1/30 s Tính từ lúc lúc t = 0, vận tốc xấp xỉ của điểm M là:
A. 10,9 m/s B. 6,3 m/s C. 4,4 m/s D. 7,7 m/s
Hướng dẫn giải:
Ta có: 2λ = 80cm λ = 40cm
Xét 1 thành phần bụng B gần M nhất trên sợi dây, từ đồ thị ta thấy:
Tại thời gian t = O, B ở biên dương uB1 = 4cm. Sau thời hạn ngắn nhất t2 = t, B có li độ uB2 = u0. Tại thời gian t3 = 3t, B có li độ uB3 = – u0.
Sử dụng vòng tròn lượng giác ta có: β = ω.(t3 t2) = ω.2t; α = ω.t β = 2α
Mà β = 2(π/2 α) = π – 2α β = π/2; α = π/4
Suy ra
Chu kỳ sóng: T = λ/vs = 0,4/20 = 0,02s.
M xấp xỉ đồng pha với B nên tại thời gian t = 0, B ở biên dương thì M cũng ở biên dương, do đó AM = 22 cm.
Khoảng thời hạn t = 1/30s = T + 2T/3 thì M có li độ là uM = -AM/2 (dùng vòng tròn lượng giác).
Tốc độ của M khi đó là: |vM| = 3/2 ω.AM = 3/2 . 2π/T . 22 = 769,5 cm/s = 7,7 m/s
Ví dụ 3: Một sợi dây đang sẵn có sóng dừng ổn định. Sóng truyền trên dây có tần số 10Hz và bước sóng 6cm. Trên dây, hai thành phần M và N có vị trí cân đối phương pháp nhau 8cm, M thuộc một bụng sóng xấp xỉ điều hòa với biên độ 6mm. Lấy π2 = 10. Tại thời gian t, thành phần M đang hoạt động và sinh hoạt giải trí với vận tốc 6π2 cm/s thì thành phần N hoạt động và sinh hoạt giải trí với tần suất có độ lớn là:
A. 63 m/s2. B. 62 m/s2. C. 6 m/s2. D. 3m/s2.
Hướng dẫn giải:
Chọn B
M là bụng sóng, N cách bụng M một khoảng chừng d = 8cm, ta thấy M và N xấp xỉ ngược pha, biên độ xấp xỉ của N là:
Tại thời gian t, thành phần M đang hoạt động và sinh hoạt giải trí với vận tốc |vM| = 6π2 cm/s thì có độ lớn li độ uM thỏa mãn nhu cầu:
M và N xấp xỉ ngược pha nên
Gia tốc của thành phần N có độ lớn là:
|aN| = |-ω2.uN| = ω2.|uN| = 6002 cm/s2 = 62 m/s2
b) Khoảng thời hạn li độ, vận tốc lặp lại, hình dạng sợi dây lặp lại.
* Giả sử trên sợi dây ta có 3 điểm sau: N là nút, P là bụng sóng gần N nhất, Q. là yếu tố nằm trong tâm N và P, biết QN = d1.
Biên độ của điểm Q. là: AQ = 2A sin (2πd1/λ)
Khoảng thời hạn giữa hai lần liên tục để độ lớn li độ của P bằng biên độ của điểm C là t
ứng với góc quét φ1 hoặc góc quét φ2.
Từ hình vẽ ta xác lập được φ1 và φ2:
Suy ra khoảng chừng thời hạn cần xác lập là: t = φ1/ω hoặc t = φ2/ω .
* Trường hợp P và Q. có cùng li độ chỉ xẩy ra khi chúng trải qua VTCB, do vậy khoảng chừng thời hạn liên tục giữa hai lần P và Q. co cùng li độ là T/2.
Ví dụ 4: (Quốc gia 2011) Một sợi dây đàn hồi căng ngang, đang sẵn có sóng dừng ổn định. Trên dây, A là một điểm nút, B là một điểm bụng gần A nhất, C là trung điểm của AB, với AB = 10 cm. Biết khoảng chừng thời hạn ngắn nhất giữa hai lần mà li độ xấp xỉ của thành phần tại B bằng biên độ xấp xỉ của thành phần tại C là 0,2 s. Tốc độ truyền sóng trên dây là
A. 2 m/s. B. 0,5 m/s. C. 1 m/s. D. 0,25 m/s.
Hướng dẫn giải:
Bước sóng của sóng truyền trên dây: λ = 4.AB = 40cm.
Biên độ của thành phần tại C:
Từ hình vẽ ta cũng tính được góc quét φ ứng với mức chừng thời hạn ngắn nhất li độ của B bằng biên độ của C là:φ1 = 2 arccos AC/AB = π/2= φ2 ứng với mức chừng thời hạn là T/4
Suy ra T/4 = 0,2s T = 0,8s.
Ta tính được vận tốc truyền sóng trên dây: v = λ/T = 50cm/s = 0,5m/s.
Câu 1: Một sóng dừng trên dây có dạng u = 2sin(bx).cos(10πt + π) (cm). Trong số đó u là li độ tại thời gian t của thành phần M trên dây, x tính bằng cm, là khoảng chừng cách từ nút O của dây tới điểm M. Tốc độ truyền sóng trên dây là 30 cm/s. Giá trị của b là:
A. 100π/3 (rad/cm). B. 0,1π/3 (rad/cm). C. π/3 (rad/cm). D. 10π/3 (rad/cm)
Hiển thị lời giải
Sử dụng công thức tính vận tốc truyền sóng: v=(Hệ số của t)/(Hệ số của x)
Ta được:
Câu 2: Một sóng dừng trên dây có dạng u = asin(bx).cos(10πt + π/2) (cm). Trong số đó u là li độ tại thời gian t của thành phần M trên dây, x tính bằng cm, là khoảng chừng cách từ nút O của dây tới điểm M. Tốc độ truyền sóng trên dây là 20 cm/s. Tại điểm cách nút 0,5 cm có biên độ sóng 2cm. Độ lớn của a là:
A. 32 cm B. 22 cm . C. 23 cm D. 3cm
Hiển thị lời giải
Chọn B
Ta có: vận tốc truyền sóng: v=(Hệ số của t)/(Hệ số của x)
Biên độ sóng tại điểm cách nút d = 0,5 cm: A = asin(bx)
Câu 3: Sóng dừng trên một sợi dây có biên độ ở bụng là 5cm. Giữa hai điểm M, N có biên độ 2,5cm cách nhau x = 20cm những điểm luôn xấp xỉ với biên độ nhỏ hơn 2,5cm. Bước sóng là.
A. 60 cm B. 12 cm C. 6 cm D. 120 cm
Hiển thị lời giải
Chọn D
Do những điểm giữa M, N đều phải có biên độ nhỏ hơn biên độ xấp xỉ tại M, N nên chúng là hai điểm gần nhau nhất đối xứng qua một nút sóng.
Suy ra khoảng chừng cách từ M đến nút gàn nhất là: d = MN/2 = 20/2 = 10cm.
Biên độ doa động của điểm M là: AM = 2A.sin2πd/λ
2,5 = 5.sin 2π10/λ
=> 2π10/λ = π/6
=> λ = 120 cm
Câu 4: Một sợi dây đàn hồi OM = 90 cm có hai đầu cố định và thắt chặt. Khi được kích thích thì trên dây có sóng dừng với 3 bó sóng. Biên độ tại bụng sóng là 3 cm. Tại điểm N trên dây gần O nhất có biên độ xấp xỉ là một trong,5 cm. ON có mức giá trị là :
A. 5 cm B. 15 cm C. 52 cm D. 7,5 cm
Hiển thị lời giải
Chọn A
Dây hai đầu cố định và thắt chặt, có sóng dừng với 3 bó sóng nên OM = 90cm = 3.λ/2
λ = 60cm.
Vì O là nút sóng nên biên độ của N được xem bằng công thức: AN = 2A.sin2πON/λ
=> 1,5 = 3sin 2πON/60 => ON = 5 cm.
Câu 5: Trong thí nghiệm về sự việc phản xạ sóng trên vật cản cố định và thắt chặt. Sợi dây mền AB có đầu B cố định và thắt chặt, đầu A xấp xỉ điều hòa. Ba điểm M, N, P không phải là nút sóng, nằm trên sợi dây cách nhau MN = λ/2; MP = l. Khi điểm M trải qua vị trí cân đối (VTCB) thì
A. điểm N có li độ cực lớn, điểm P trải qua VTCB.
B. N trải qua VTCB, điểm P có li độ cực lớn.
C. điểm N và điểm P trải qua VTCB.
D. điểm N có li độ cực tiểu, điểm P có li độ cực lớn.
Hiển thị lời giải
Chọn C
Vì M, P không phải nút sóng và MP = λ, do đó M và P nằm cách nhau 1 bó M xấp xỉ đồng pha với P.
MN = λ/2 < MP nên N nằm trong tâm M và P, đồng thời N nằm ở vị trí bó giữa nên N xấp xỉ ngược pha với M và P.
Suy ra: Khi điểm M trải qua vị trí cân đối (VTCB) thì P trải qua VTCB và N cũng trải qua VTCB theo chiều ngược lại.
Câu 6: Một dây đàn hồi AB đầu A được rung nhờ một dụng cụ để tạo thành sóng dừng trên dây, biết phương trình xấp xỉ tại đầu A là uA = acos100t. Quan sát sóng dừng trên sợi dây ta thấy trên dây có những điểm không phải là yếu tố bụng xấp xỉ với biên độ b (b 0) cách đều nhau và cách nhau khoảng chừng 1m. Giá trị của b và tốc truyền sóng trên sợi dây lần lượt là:
A. a2 ; v = 200m/s. B. a3 ; v = 150m/s.
C. a; v = 300m/s. D. a2 ; v = 100m/s.
Hiển thị lời giải
Chọn A
Những điểm cách đều nhau liên tục (không kể bụng và nút) có cùng biên độ xấp xỉ sẽ cách nhau 1 khoảng chừng nhỏ nhất là /4 và cùng biên độ .
λ = 4m v = λ.f = 200m/s
Câu 7: Một sợi dây AB = 120 cm, hai đầu cố định và thắt chặt, khi có sóng dừng ổn định xuất hiện 5 nút sóng. O là trung điểm dây, M, N là hai điểm trên dây nằm về hai phía của O, với OM = 5cm, ON = 10 cm, tại thời gian t vận tốc của M là 60 cm/s thì vận tốc của N là
A. -603 cm/s B. 602 cm/s C. 303 cm/s D. – 60cm/s
Hiển thị lời giải
Chọn A
Dây AB = 120 cm, hai đầu cố định và thắt chặt, khi có sóng dừng ổn định xuất hiện 5 nút sóng nên trên dây có 4 bó sóng 120cm = 4λ/2 λ = 60cm.
O là trung điểm dây AB nên OA = 60cm = 2.λ/2 nên O là nút thứ 3 tính từ nút A.
Ta có: OM = 5cm < λ/4 = 15cm; ON = 10cm < λ/2 nên M và N xấp xỉ ngược pha (M và N nằm trên 2 bó liền kề).
Câu 8: Một sóng dừng trên dây có bước sóng λ và N là một nút sóng. Hai điểm P, Q. nằm về 2 phía của N và có vị trí cân đối phương pháp N những đoạn lần lượt là λ/8 và λ/12 . Ở cùng một thời điểm mà hai phần tử tại đó có li độ khác không thì tỉ số giữa li độ của P so với Q. là
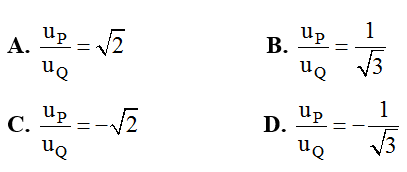
Chọn C
Ta nhận thấy M1 và M2 xấp xỉ ngược pha.
Suy ra:
Câu 9: Một sóng dừng trên một sợi dây có dạng u = 40sin(2,5πx)cosωt (mm), trong số đó u là li độ tại thời gian t của một điểm M trên sợi dây mà vị trí cân đối của nó cách gốc tọa độ O đoạn x (x tính bằng mét, t đo bằng s). Khoảng thời hạn ngắn nhất giữa hai lần liên tục để một chất điểm trên bụng sóng có độ lớn li độ bằng biên độ của điểm N cách nút sóng 10cm là 0,125s. Tốc độ truyền sóng trên sợi dây là:
A. 320cm/s B. 160cm/s C. 80cm/s D. 100cm/s
Hiển thị lời giải
Chọn B
Bước sóng của sóng truyền trên dây: 2,5πx = 2πx/λ => λ = 2/2,5 = = 0,8m = 80cm
Biên độ của phần từ tại N: AN = 40|sin(2π.10/80)| = 202mm
Từ hình vẽ ta cũng tính được góc quét φ ứng với mức chừng thời hạn ngắn nhất li độ của B bằng biên độ của C là: φ1 = 2 arccos 202/40 = π/2 = φ2 ứng với mức chừng thời hạn là T/4
Suy ra T/4 = 0,125s T = 0,5s.
Ta tính được vận tốc truyền sóng trên dây: v = λ/T = 160cm/s.
Câu 10: Sóng dừng xuất hiện trên sợi dây với tần số f = 5Hz. Gọi thứ tự những điểm thuộc dây lần lượt là O, M, N, P sao cho O là yếu tố nút, P là yếu tố bụng sóng gần O nhất (M, N thuộc đoạn OP). Khoảng thời hạn giữa 2 lần liên tục để giá trị li độ của điểm P bằng biên độ xấp xỉ của điểm M, N lần lượt là một trong/15s và 1/20s. Biết khoảng chừng cách giữa 2 điểm M, N là 0,2cm. Bước sóng của sợi dây là:
A. 5,6cm B. 4,8 cm C. 1,2cm D. 2,4cm
Hiển thị lời giải
Chọn B
Biên độ của thành phần tại M và N lần lượt là:
AM = 2Asin(2πOM/λ) ; AN = 2Asin(2πON/λ) (1)
Vì OM < ON < OP = λ/4 nên AM < AN.
Sử dụng vòng tròn lượng giác màn biểu diễn xấp xỉ điều hòa của thành phần bụng P.
Các góc quét α, β tương ứng với những khoảng chừng thời hạn 1/15s và 1/20s
α = ω.t1 = 10π.1/15 = 2π/3; β = ω.t2 = 10π.1/20 = π/2.
Mặt khác:
Từ (1) suy ra OM = λ/12; ON = λ/8
Khoảng cách giữa 2 điểm M, N là 0,2cm ON OM = λ/24 = 0,2cm λ = 4,8cm.
Câu 11: M, N, P là 3 điểm liên tục nhau trên một sợi dây mang sóng dừng có cùng biên độ 4cm, xấp xỉ tại P ngược pha với xấp xỉ tại M. MN = 2NP = 20cm. Cứ sau khoảng chừng thời hạn ngắn nhất là 0,04s sợi dây lại sở hữu dạng một đoạn thẳng. Tính vận tốc xấp xỉ tại điểm bụng khi sợi dây có dạng một đoạn thẳng.
A. 6,28m/s B. 62,8cm/s C. 125,7cm/s D. 3,14m/s
Hiển thị lời giải
Chọn D
Vì M, N, P liên tục nhau có cùng biên độ, P ngược pha với M, MN = 20cm > NP = 10cm nên M và N nằm trên cùng 1 bó, P nằm trên bó tiếp theo. Khi đó N và P đối xứng nhau qua nút C sớm nhất ở giữa N và P.
NC = CP = NP/2 = 5cm.
N và M đồng pha trên 1 bó nên N và M đối xứng nhau qua bụng B sớm nhất.
NB = MB = MN/2 = 10cm
Mặt khác BC = NB + NC = 15cm = λ/4 λ = 60cm.
Ta có biên độ sóng tại N là: AN = 2A sin(2πNC/λ) = 2A sin2π.5/60 = A = 4cm
Khoảng thời hạn ngắn nhất sợi dây lại sở hữu dạng một đoạn thẳng là: T/4 = 0,04s
T = 0,16s ω = 12,5π rad/s.
Tốc độ xấp xỉ tại điểm bụng khi sợi dây có dạng một đoạn thẳng là vmax.
vmax =2A.ω = 100π cm/s = 3,14m/s.
Câu 12: Sóng dừng tạo trên một sợi dây đàn hồi có chiều dài l. Người ta thấy trên dây có những điểm xấp xỉ cách nhau l1 thì xấp xỉ với biên độ 4 cm, người ta lại thấy những điểm cứ cách nhau một khoảng chừng l2 (l2 > l1) thì những điểm đó có cùng biên độ a. Giá trị của a là:
A. 42 cm B. 4cm C. 22 cm D. 2cm
Hiển thị lời giải
Chọn A
– Các điểm bụng có cùng biên độ Amax = 2A nằm cách đều nhau những khoảng chừng d = λ/2.
– Những điểm cách đều nhau liên tục (không kể bụng và nút) có cùng biên độ xấp xỉ sẽ cách nhau 1 khoảng chừng nhỏ nhất là λ/4 và cùng biên độ A2 .
Như vậy vì l2 > l1 nên l2 = λ/2, l1 = λ/4.
Suy ra: a = Amax = 2A, A2 = 4cm => A = 22cm => a = 42cm
Câu 13: Sóng dừng tạo trên một sợi dây đàn hồi có chiều dài l. Người ta thấy trên dây có những điểm xấp xỉ cách nhau l1 thì xấp xỉ với biên độ a1 người ta lại thấy những điểm cứ cách nhau một khoảng chừng l2 thì những điểm đó có cùng biên độ a2 (a2 < a1) Tỉ số l2/l1 là:
A. 2 B. 1/2 C. 1 D. 0,25
Hiển thị lời giải
Chọn B
– Các điểm bụng có cùng biên độ Amax = 2A nằm cách đều nhau những khoảng chừng d = λ/2.
– Những điểm cách đều nhau liên tục (không kể bụng và nút) có cùng biên độ xấp xỉ sẽ cách nhau 1 khoảng chừng nhỏ nhất là λ/4 và cùng biên độ A2 .
Theo đề bài a2 < a1 nên a2 = A2 và a1 = Amax = 2A.
Suy ra l1 = λ/2, l2 = λ/4
=> l2/l1 = 1/2
Câu 14: Sóng dừng tạo trên một sợi dây đàn hồi có chiều dài l với hai đầu tự do. Người ta thấy trên dây có những điểm xấp xỉ cách nhau l1 = 1/16 thì xấp xỉ với biên độ a1 người ta lại thấy những điểm cứ cách nhau một khoảng chừng l2 thì những điểm đó có cùng biên độ a2 (a2 > a1) Số điểm bụng trên dây là:
A. 9 B. 8 C. 5 D. 4
Hiển thị lời giải
Chọn A
– Các điểm bụng có cùng biên độ Amax = 2A nằm cách đều nhau những khoảng chừng d = λ/2.
– Những điểm cách đều nhau liên tục (không kể bụng và nút) có cùng biên độ xấp xỉ sẽ cách nhau 1 khoảng chừng nhỏ nhất là λ/4 và cùng biên độ A2 .
Ta có a2 > a1 nên l1 = l/16 = λ/4; l2 = λ/2 => l = 4λ
Sợi dây đàn hồi có chiều dài l với hai đầu tự do và l = 4λ = λ/4 + 7 λ/2 + λ/4
Số bụng sóng trên dây (tính cả hai đầu) là 7 + 2 = 9 bụng.
Câu 15: Một sợi dây AB đàn hồi căng ngang dài l = 120cm, hai đầu cố định và thắt chặt đang sẵn có sóng dừng ổn định. Bề rộng của bụng sóng là 4a. Khoảng cách sớm nhất giữa hai điểm xấp xỉ cùng pha có cùng biên độ bằng a là 20 cm. Số bụng sóng trên AB là
A. 4. B. 8. C. 6. D. 10.
Hiển thị lời giải
Chọn A
Bề rộng của bụng sóng là 4a nên nguồn sóng xấp xỉ với biên độ là a.
Hai điểm gần nhau nhất xấp xỉ cùng pha có cùng biên độ bằng a là 20 cm nên hai điểm này đối xứng nhau qua bụng, do đó khoảng chừng cách từ hai điểm này đến bụng sớm nhất là:
d = 20/2 = 10cm.
Biên độ những điểm này: AN = 2a cos(2π.10/λ) = a
> 20π/λ = π/3 => λ = 60 cm
Một sợi dây AB đàn hồi có hai đầu cố định và thắt chặt và l = 120cm = 4λ/2 nên trên dây có 4 bụng sóng.
Câu 16: Cho sợi dây một đầu cố định và thắt chặt, một đầu còn sót lại gắn với cần rung phát sóng xấp xỉ với phương trình uo = acos(ωt + φ) cm. Trên dây có sóng dừng ổn định với bước sóng λ. Hai điểm M và N trên dây cách nhau 3,75λ có biên độ lần lượt là AM = 6cm; AN = 8cm. Tìm biên độ của nguồn phát ra sóng đó ?
A. a = 10cm. B. a = 7,5cm. C. a = 11cm. D. a = 5cm
Hiển thị lời giải
Chọn D
Gọi d1, d2 lần lượt là khoảng chừng cách từ M, N tới đầu nút cố định và thắt chặt, ta có: d1 d2 = 3,75λ.
Biên độ của bụng sóng là Ab = 2a.
Biên độ sóng dừng tại M và N lần lượt là:
Do đó ta được:
Câu 17: Một sợi dây đàn hồi căng ngang, đang sẵn có sóng dừng 2 đầu cố định và thắt chặt. Trên dây, A là một nút, B là yếu tố bụng gần A nhất với AB = 15cm. M là một điểm trên dây cách B là 10cm. Biết rằng trong một chu kỳ luân hồi sóng, khoảng chừng thời hạn mà độ lớn vận tốc xấp xỉ của thành phần B to nhiều hơn vận tốc xấp xỉ cực lớn của thành phần M là 2/3s. Tốc độ truyền sóng trên dây là:
A . 240cm/s B. 120cm/s C. 60cm/s D. 80cm/s
Hiển thị lời giải
Chọn C
A là một nút, B là yếu tố bụng gần A nhất với AB = 15cm λ/4 = 15cm λ = 60cm.
Biên độ xấp xỉ của M là:
Vận tốc xấp xỉ cực lớn của thành phần M là: vmax(M) = AM.ω = vmax(B)/2.
Sử dụng vòng tròn lượng giác màn biểu diễn vận tốc xấp xỉ vB của thành phần sóng tại B, ta thấy khoảng chừng thời hạn trong một chu kỳ luân hồi xấp xỉ sóng mà độ lớn vận tốc xấp xỉ của thành phần B to nhiều hơn vận tốc xấp xỉ cực lớn của thành phần M ứng với 2 cung quét như trên hình.
Từ hình học ta suy ra khoảng chừng thời hạn thỏa mãn nhu cầu là 2T/3 = 2/3s T = 1s.
Tốc độ truyền sóng trên dây là: v = λ/T = 60cm/s.
Câu 18: (Quốc gia 2014) Trên một sợi dây đàn hồi đang sẵn có sóng dừng ổn định với mức chừng cách giữa hai nút sóng liên tục là 6 cm. Trên dây có những thành phần sóng xấp xỉ với tần số 5 Hz và biên độ lớn số 1 là 3 cm. Gọi N là vị trí của một nút sóng; C và D là hai thành phần trên dây ở hai bên của N và có vị trí cân đối phương pháp N lần lượt là 10,5 cm và 7 cm. Tại thời gian t1, thành phần C có li độ 1,5 cm và đang khuynh hướng về vị trí cân đối. Vào thời gian t2 = t1 + 79/40s , thành phần D có li độ là
A. 0,75 cm. B. 1,50 cm. C. 1,50 cm. D. 0,75 cm.
Hiển thị lời giải
Chọn B
Bước sóng: λ = 2.6 = 12cm; Tần số góc: ω = 10π rad/s
Biên độ xấp xỉ của những điểm cách nút một đoạn d khi có sóng dừng được xác lập bởi A = Ab|sin 2πd/λ| với Ab là biên độ xấp xỉ của điểm bụng, vậy ta có:
Hai điểm C và D thuộc những bó sóng đối xứng nhau qua nút N do vậy luôn xấp xỉ ngược pha nhau.
Thời điểm t1 C đang ở li độ uC = + 2/2 Ac => uD = -2/2 AD
Vào thời gian t2 = t1 + 79/40s , góc quét tương ứng giữa hai thời gian t1 và t2 là:
φ = ω.t = 10π.79/40 = 18π + π + 0,75π (rad).
li độ sóng tại C ở thời gian t2 là: uC = AC = 1,5 cm.
Vì C và D xấp xỉ ngược pha nên lúc đó uD = -AD = -1,5cm
Câu 19: (QG-2015): Trên một sợi dây OB căng ngang, hai đầu cố định và thắt chặt đang sẵn có sóng dừng với tần số f xác lập. Gọi M, N và P là ba điểm trên dây có vị trí cân đối phương pháp B lần lượt là 4 cm, 6 cm và 38 cm. Hình vẽ mô tả hình dạng sợi dây tại thời gian t1 (đường 1) và t2 = t1 + 11/12f (đường 2). Tại thời gian t1, li độ của thành phần dây ở N bằng biên độ của thành phần dây ở M và vận tốc của thành phần dây ở M là 60 cm/s. Tại thời gian t2, vận tốc của thành phần dây ở P là
A. 60 cm/s. B. 203 cm/s. C. -203 cm/s. D. – 60 cm/s.
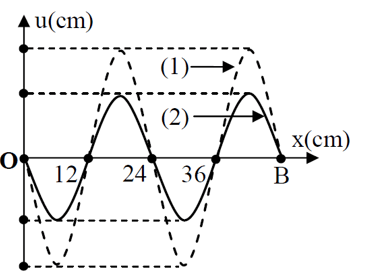
Chọn D
Theo hình vẽ ta có: λ = 24 cm.
Tính biên độ xấp xỉ của những điểm M, N, P: A = Ab.sin|2πx/λ|
(với Ab: biên độ của điểm bụng, x là khoảng chừng cách từ điểm xét tới điểm nút bất kỳ).
Thay số, ta được: AM = Ab3/2; AN = Ab; Ap = Ab/2
Dễ dàng thấy: N và M cùng pha, N và P ngược pha.
Tại thời gian t1: li độ của điểm N bằng biên độ M thì vận tốc xấp xỉ của M bằng 60 cm/s:
uN = AM = Ab3/2
=> uM = AM/AN. uN = 3/4 Ab (vì N và M cùng pha)
Tại thời gian t2 (sau t1 là 11T/12 ) hình dạng sợi dây (đường 2) có dạng như hình vẽ bên.
Tại thời gian t1 những thành phần M, N, P đang hoạt động và sinh hoạt giải trí theo chiều đi ra vị trí biên tương ứng. Vec tơ quay mô tả hoạt động và sinh hoạt giải trí của N, P tại thời gian t1 và t2:
Vậy ở thời gian t2, điểm P có li độ là up = -Ab/4 và P đang đi theo chiều âm.
Suy ra:
Câu 20: (Quốc gia 2022). Trên một sợi dây đàn hồi đang sẵn có sóng dừng ổn định. Sóng truyền trên dây có tần số 10 Hz, bước sóng 6 cm. Trên dây, hai thành phần M và N có vị trí cân đối phương pháp nhau 8 cm, M thuộc một bụng sóng xấp xỉ với biên độ 6 mm. Lấy π2 = 10. Tại thời gian t, thành phần M đang hoạt động và sinh hoạt giải trí với vận tốc 6π cm/s thì thành phần N hoạt động và sinh hoạt giải trí với tần suất có độ lớn là
A. 63 m/s2. B. 62 m/s2. C. 6 m/s2. D. 3 m/s2.
Hiển thị lời giải
+ Từ giả thuyết của bài toán ta hoàn toàn có thể xác lập được điểm N cách nút một sớm nhất một đoạn λ/12, do đó N sẽ xấp xỉ với biên độ là AN = 0,5A = 3mm.
+ Tại thời gian t, M đang hoạt động và sinh hoạt giải trí với vận tốc vN = vNmax = 6π cm/s. Biểu diễn tương ứng trên đường tròn. Hai điểm M và N nằm trên hai bó sóng đối xứng với nhau qua một nút nên xấp xỉ ngược pha.
+ Từ hình vẽ ta hoàn toàn có thể tính được, tại thời gian t, điểm N có tần suất:
Xem thêm những dạng bài tập Vật Lí lớp 12 có trong đề thi THPT Quốc gia khác:
Giới thiệu kênh Youtube Tôi
Trang trước
Trang sau
Reply
1
0
Chia sẻ
Chia Sẻ Link Down Tỉ số giữa khoảng chừng cách lớn số 1 và nhỏ nhất miễn phí
Bạn vừa tìm hiểu thêm tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Review Tỉ số giữa khoảng chừng cách lớn số 1 và nhỏ nhất tiên tiến và phát triển nhất và Chia Sẻ Link Down Tỉ số giữa khoảng chừng cách lớn số 1 và nhỏ nhất miễn phí.

Hỏi đáp vướng mắc về Tỉ số giữa khoảng chừng cách lớn số 1 và nhỏ nhất
Nếu sau khi đọc nội dung bài viết Tỉ số giữa khoảng chừng cách lớn số 1 và nhỏ nhất vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha
#Tỉ #số #giữa #khoảng chừng #cách #lớn #nhất #và #nhỏ #nhất