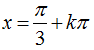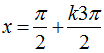Mẹo Hướng dẫn Có bao nhiêu giá trị nguyên của tham số m để phương trình sinx m có nghiệm Chi Tiết
Pro đang tìm kiếm từ khóa Có bao nhiêu giá trị nguyên của tham số m để phương trình sinx m có nghiệm được Update vào lúc : 2022-01-15 08:55:03 . Với phương châm chia sẻ Bí quyết về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Phương pháp giải phương trình lượng giác cơ bản hay, rõ ràng
Trang trước
Trang sau
Quảng cáo
+ Nếu α là một nghiệm của phương trình sinx= m thì phương trình này còn có hai họ nghiệm là:
Chú ý: phương trình sinx= m chỉ có nghiệm khi: – 1 m 1.
+ Nếu α là một nghiệm của phương trình cosx=m thì phương trình đã cho có hai họ nghiệm:
+ Nếu α là một nghiệm của phương trình tanx= m thì phương trình này còn có nghiệm là:
x= α+kπ
+ Nếu α là một nghiệm của phương trình cot x = m thì phương trình này còn có nghiệm là:
x= α+kπ
+ Các trường hợp đặc biệt quan trọng :
Sinx=0 x=kπ
Sinx= 1 x= π/2+k2π
Sinx= -1 x= (-π)/2+k2π
cos= 0 x= π/2+kπ
cosx= 1 x=k2π
cosx=- 1 x= π+k2π
Ví dụ 1. Hỏi x=7π/3 là nghiệm của phương trình nào sau này?
A. 2sinx – 3=0.
B. 2sinx+ 3=0.
C. 2cosx- 3=0
D.2cosx+ 3=0.
Lời giải
Chọn A
Cách 1.
Với x=7π/3 , suy ra .
Cách 2. Thử x=7π/3 lần lượt vào những phương trình.
Ví dụ 2. Giải phương trình sin(2x/3- π/3)=0.
A. x=kπ (kZ)
B. .
C. .
D. .
Lời giải.
Chọn D.
Ta có : sin(2x/3- π/3)=0.
2x/3- π/3=kπ (kZ)
2x/3= π/3+kπ x= π/2+ k3π/2 ( kZ).
Quảng cáo
Ví dụ 3. Với giá trị nào của x thì giá trị của những hàm số y= sin3x và y= sinx bằng nhau?
A.
B.
C.
D.
Lời Giải.
Chọn B.
Xét phương trình hoành độ giao điểm của hai đồ thị: sin 3x= sinx
Ví dụ 4. Giải phương trình cot(3x-1)= -3
A.
B.
C.
D.
Lời Giải.
Chọn A.
Ta có cot(3x-1)= -3 cot(3x-1)= cot(-π/6) .
3x-1= (-π)/6+kπ x= 1/3- π/(18 )+k. π/3 = 1/3+ 5π/(18 )+(k-1). π/3
Đặt k- 1=l suy ra nghiệm phương trình x= 1/3+ 5π/(18 )+l. π/3
Ví dụ 5. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình tanx = 1?
A. sinx= 2/2
B. sinx= 2/2
C. cotx= 1
D.cot2x = 1
Lời giải
Chọn C.
Ta có: tanx=1 x= π/4+kπ ( kZ).
Xét đáp án C, ta có cotx=1 x= π/4+kπ ( kZ).
Cách 2. Ta có đẳng thức tanx=1/cotx . Kết hợp giả thiết tanx=1, ta được cotx=1. Vậy hai phương trình tanx= 1 và cotx= 1 là tương tự.
Quảng cáo
Ví dụ 6. Có bao nhiêu giá trị nguyên của tham số m để phương trình cosx= m+ 1 có nghiệm?
A. 1
B. 2
C. 3
D. Vô số.
Lời giải
Chọn C.
Áp dụng Đk có nghiệm của phương trình cosx= a.
+ Phương trình có nghiệm khi |a| 1.
+Phương trình vô nghiệm khi |a| > 1.
Do đó, phương trình cosx= m+ 1 có nghiệm khi và chỉ khi
Vậy có 3 giá trị nguyên của m để phương trình đã cho có nghiệm.
Ví dụ 7. Gọi S là tập hợp toàn bộ những giá trị nguyên của tham số m để phương trình
cos(2x- π/3)-m=2 có nghiệm. Tính tổng T của những thành phần trong S.
A. T= 6
B. T=3
C. T= – 3
D. T= – 6
Lời giải
Chọn D.
Phương trình cos(2x- π/3)-m=2 cos(2x- π/3)= m+2.
Phương trình có nghiệm khi và chỉ khi:
– 1 m+2 1 – 3 m -1.
Mà m nguyên nên m-3;-2;-1
Suy ra: T= – 3+ ( -2)+ (-1)= – 6
Ví dụ 8. Giải phương trình: tan(π/3+x)=tan π/4
A. -π/12+kπ
B. π/12+kπ
C. -π/3+kπ
D. -π/4+kπ
Lời giải
Ta có: tan(π/3+x)=tan π/4
π/3+x= π/4+kπ ( kZ)
x= π/4- π/3+kπ= (-π)/12+kπ
Chọn D .
Ví dụ 9. Giải phương trình: cos((x+ π)/4)= 1/2
A. x= π/3+4kπ hoặc x= (- π)/3+k4π)
B. x= π/12+4kπ hoặc x= (- π)/12+k4π)
C. x= π/3+4kπ hoặc x= (- 7π)/3+k4π)
D. Đáp án khác
Lời giải
Ta có: cos((x+ π)/4)= 1/2 hay cos((x+ π)/4)= cos π/3
Chọn C
Ví dụ 10. Giải phương trình : sinx= 2/5
A. x= α+k2π hoặc x= – α+k2π
B. x= α+k2π hoặc x= π+ α+k2π
C. x= α+kπ hoặc x= π- α+kπ
D. x= α+k2π hoặc x= π- α+k2π
Với sinα= 2/5
Lời giải
Vì – 1 < 2/5 < 1 nên có số α để sinα = 2/5
Khi đó sinx= 2/5 sinx= sinα nên x= α+k2π hoặc x= π- α+k2π
Chọn D
Ví dụ 11. Giải phương trình tanx= 2
A. 2+ kπ
B. arctan 2+ kπ
C.2+ k2π
D. arctan 2+ k 2π
Lời giải
Ta có: tanx = 2 x= arctan2+ kπ ( kZ)
Chọn B.
Ví dụ 12. Giải phương trình : cot(π/3+x)=cot(π+x)/2
A. π/3+ k4π
B. π/3+ k2π
C. π/3+ kπ
D. π/6+ kπ
Lời giải
Ta có: cot(π/3+x)=cot (π+x)/2
π/3+x= (π+x)/2+kπ với kZ
x- x/2= π/2- π/3+kπ
x/2= π/6+kπ x=π/3+ k2π
Chọn B.
Ví dụ 13. Giải phương trình cos(400+ x)= cos( 800 x)
A. x= 200+ k. 1800
B. x= 200+ k. 3600
C. x= – 400+ k.1800
D. Cả A và C đúng
Lời giải
Ta có: cos( 400+ x) = cos( 800 x)
Chọn A.
Ví dụ 14. Giải phương trình: cos(x+ 100) = 1/3
A.
B.
C.
D.
Lời giải
Ta có: cos( x+100) = 1/3
Chọn C.
Câu 1:Giải phương trình cos(π/3-x)=0
A. – π/2+l2π
B. – π/3+l2π
C. π/6+l2π
D. – π/6+l2π
Hiển thị lời giải
Ta có: cos(π/3-x)=0
cos(π/3-x) = cos π/2
π/3-x= π/2 + k2π
-x= π/2- π/3+k2π
– x= π/6+k2π x= – π/6- k2π
Vậy tập nghiệm của phương trình đã cho là x= – π/6 + l2π ( với l= – k và nguyên )
Chọn D.
Câu 2:Phương trình: sin( 2x/3- π/3)=0 có nghiệm là:
A.
B.x=kπ .
C.
D.
Hiển thị lời giải
Chọn D.
sin( 2x/3- π/3)=0 2x/3- π/3=kπ
2x/3 = π/3+ kπ x= π/2+k3π/2
Câu 3:Nghiệm của phương trình: sinx.(2cosx-3)=0 là:
A.
B.
C.
D.
Hiển thị lời giải
Chọn A
D.
Câu 4:Cho phương trình sin(x-100) = 2m+ 1. Có bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm ?
A. 1
B.2
C. 3
D .4
Hiển thị lời giải
Ta có: phương trình sin(x-100)= 2m+1 có nghiệm khi và chỉ khi:
– 1 2m+1 1
-2 2m 0 – 1 m 0
có hai giá trị nguyên của m để phương trình đã cho có nghiệm là m= -1 hoặc m = 0
Chọn B.
Câu 5:Giải phương trình sinx= -1/3
A.
B.
C.
D.
Hiển thị lời giải
Chọn C.
Ta có: sinx=-1/3
D.
Câu 6:Giải phương trình cot x = 3
A. arccot 3 + k. π ( kZ)
B. arctan 3 + k. π ( kZ)
C. arccot 3 + k. 2π ( kZ)
D. – arccot 3 + k. π ( kZ)
Hiển thị lời giải
Ta có: cotx = 3
x= arccot 3 + k. π ( kZ)
Chọn A.
Câu 7:Giải phương trình cos(x+ π)/3= (- 1)/2
A.
B.
C.
D.
Hiển thị lời giải
Chọn B
Câu 8:Giải phưởng trình sinx=sin(2x- π/3)
A.
B.
C.
D.
Hiển thị lời giải
Chọn D.
Câu 9:
Hiển thị lời giải
Câu 10:Giải phương trình tanx=(- 3)/3
A. – π/6+kπ
B. π/6+kπ
C. – π/3+kπ
D. π/3+k2π
Hiển thị lời giải
Ta có: tanx= (- 3)/3
tanx= tan(- π)/6
x= – π/6+kπ
Chọn A.
Câu 11:Giải phương trình cot( x- π/2)=cot( (π/4-x)
A. 3π/8+kπ
B. 3π/8+kπ/2
C. 3π/4+kπ/2
D. 3π/4+kπ
Hiển thị lời giải
Ta có: cot( x- π/2)=cot( (π/4-x))
x- π/2= π/4-x+kπ
2x= 3π/4+kπ x= 3π/8+kπ/2
Chọn B.
Câu 12:Giải phương trình tanx = cot( x+ π/3)
A. π/12+ kπ
B. π/6+ kπ/2
C. π/12- kπ/2
D. π/3+ kπ
Hiển thị lời giải
Lời giải
Ta có: tanx= cot( x+ π/3)
cot(π/2-x) = cot(x+ π/3)
π/2- x = x+ π/3+kπ
– 2x= (-π)/6+kπ
x= π/12- kπ/2
Chọn C.
Câu 13:Giải phương trình sinx = cosx
A. π/4+k2π
B. π/4+kπ
C. π/2+kπ
D. Đáp án khác
Hiển thị lời giải
Lời giải
Ta có: sinx = cosx
sinx= sin(π/2-x)
.
Chọn B.
Câu 14:Nghiệm của phương trình sin3x= cosx là:
A. .
B. .
C.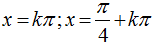
D.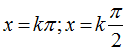
Hiển thị lời giải
Lời giải
Chọn A.
Ta có: sin3x= cosx
.
Xem thêm những dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:
Giới thiệu kênh Youtube Tôi
Trang trước
Trang sau
Reply
6
0
Chia sẻ
Share Link Tải Có bao nhiêu giá trị nguyên của tham số m để phương trình sinx m có nghiệm miễn phí
Bạn vừa đọc Post Với Một số hướng dẫn một cách rõ ràng hơn về Video Có bao nhiêu giá trị nguyên của tham số m để phương trình sinx m có nghiệm tiên tiến và phát triển nhất và ShareLink Tải Có bao nhiêu giá trị nguyên của tham số m để phương trình sinx m có nghiệm Free.

Hỏi đáp vướng mắc về Có bao nhiêu giá trị nguyên của tham số m để phương trình sinx m có nghiệm
Nếu sau khi đọc nội dung bài viết Có bao nhiêu giá trị nguyên của tham số m để phương trình sinx m có nghiệm vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Ad lý giải và hướng dẫn lại nha
#Có #bao #nhiêu #giá #trị #nguyên #của #tham #số #để #phương #trình #sinx #có #nghiệm