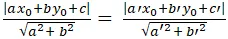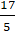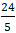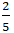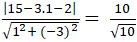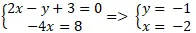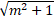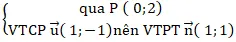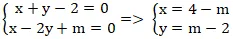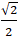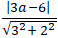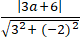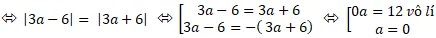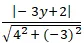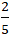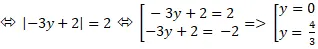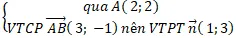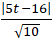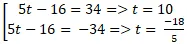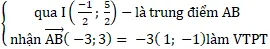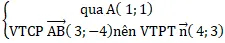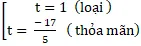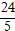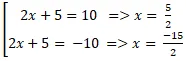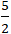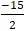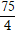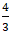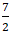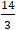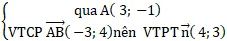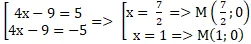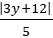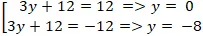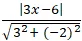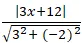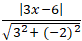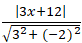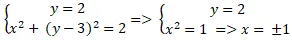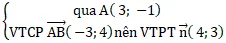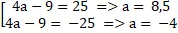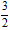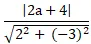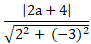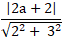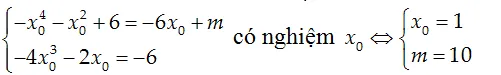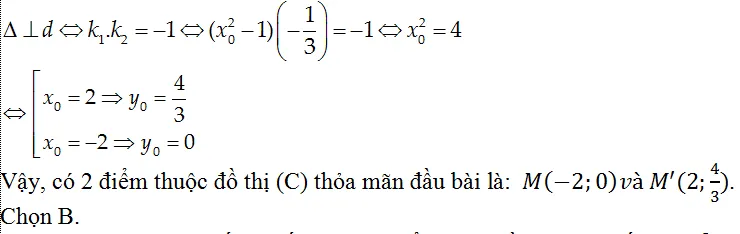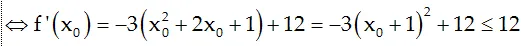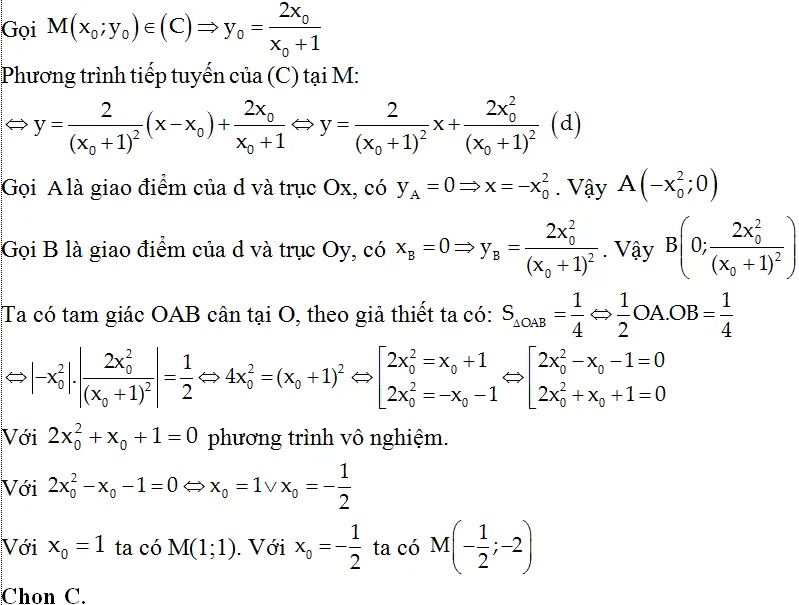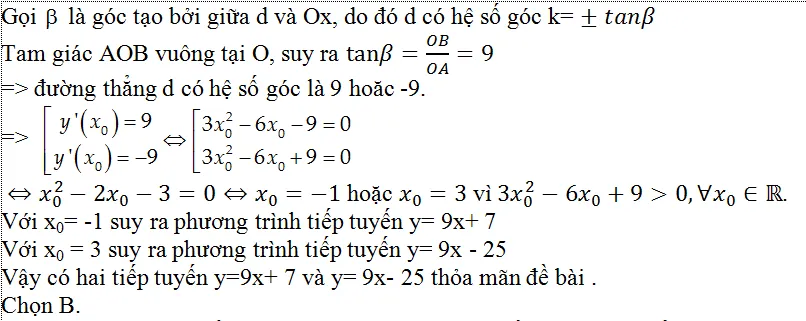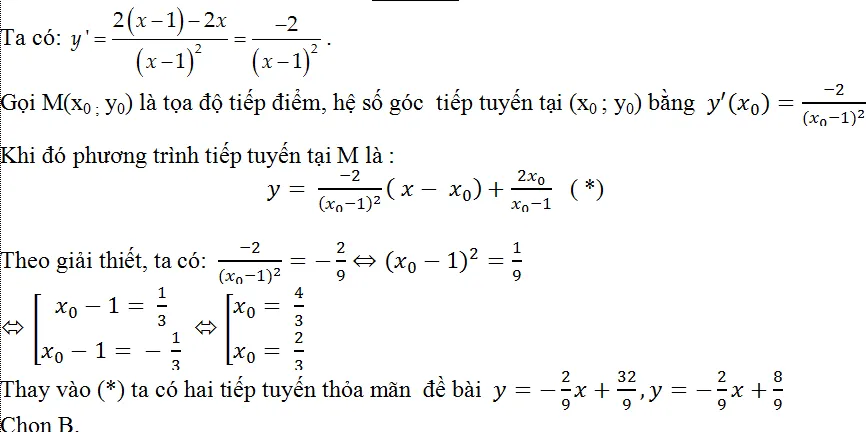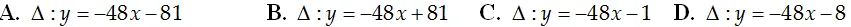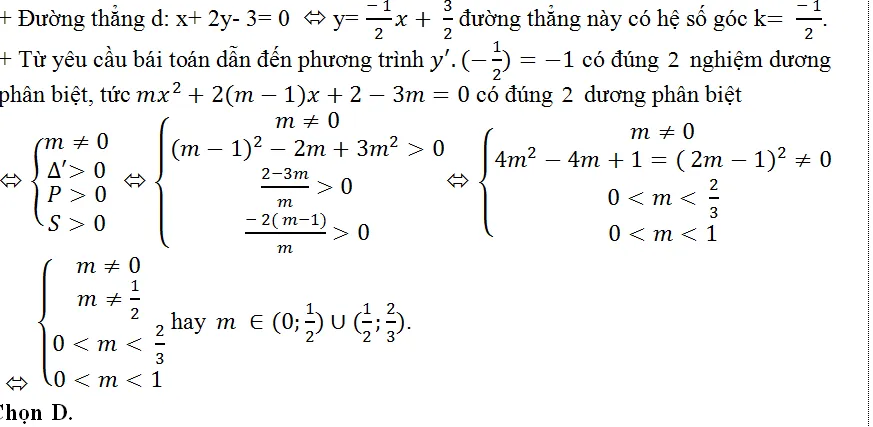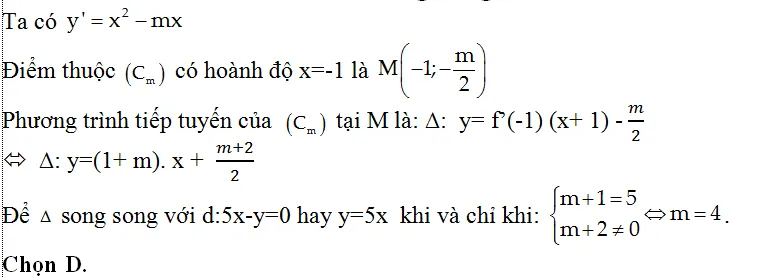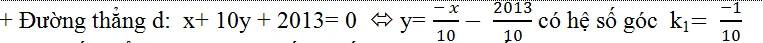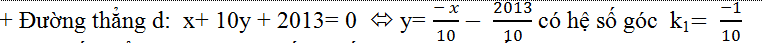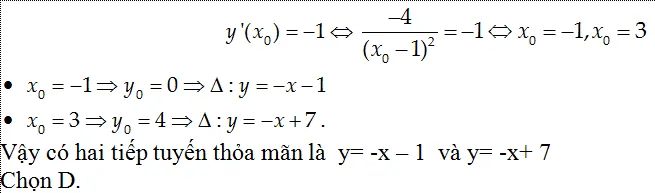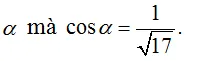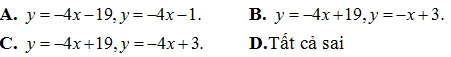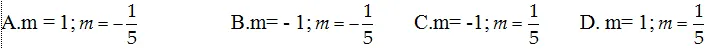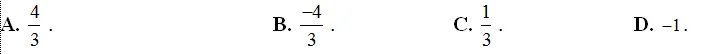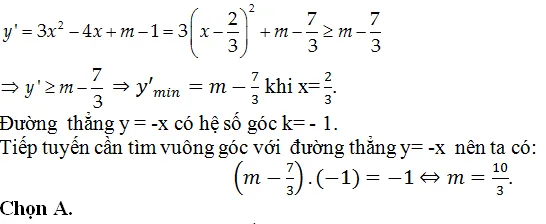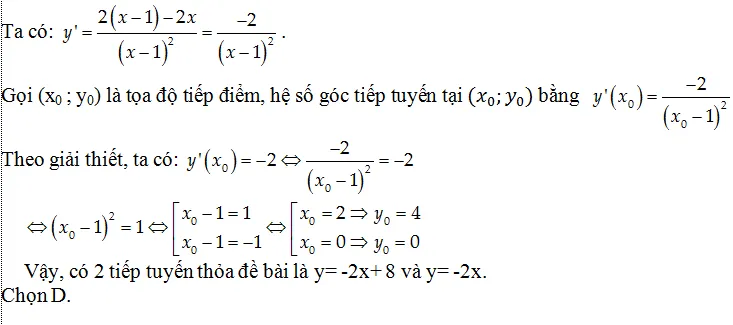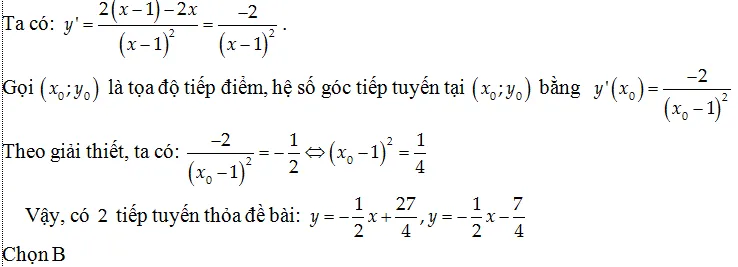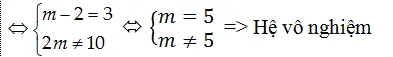Thủ Thuật về Cho đường thẳng d 2m – 5x y 1 + m = 0 tìm m sao cho khoảng chừng cách từ O đến d là a nhỏ nhất B lớn số 1 2022
Quý khách đang tìm kiếm từ khóa Cho đường thẳng d 2m – 5x y 1 + m = 0 tìm m sao cho khoảng chừng cách từ O đến d là a nhỏ nhất B lớn số 1 được Update vào lúc : 2022-02-20 17:55:04 . Với phương châm chia sẻ Bí kíp Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Tìm điểm thuộc đường thẳng có độ dài thỏa mãn nhu cầu Đk
Nội dung chính
- Tìm điểm thuộc đường thẳng có độ dài thỏa mãn nhu cầu Đk
- Viết phương trình tiếp tuyến của đồ thị hàm số lúc biết thông số góc
- Đáp án cần chọn là: DGọi A và B lần lượt là giao điểm của đường thẳng (d) với trục Ox, OyKhi đó, Am−1m;0,B0,−m+1Gọi H là hình chiếu của O lên đường thẳng (d) thì OH đó đó là khoảng chừng cách từ điểm O tới đường thẳng (d)Xét tam giác vuông OAB có 1OH2=1OA2+1OB2⇔OH=OA.OBOA2+OB2Suy ra OHmin⇔OA.OBOA2+OB2minTa cóOA.OBOA2+OB2=m−1m−m+1m−1m2+m−12=(m−1)2(m−1)2(1+mét vuông)=m−11+m2Theo bất đẳng thức Cauchy-Schwarz thì m−11+mét vuông≤21+m21+mét vuông=2Vậy OHmin =2 và đạt được khi m = -1
Trang trước
Trang sau
Quảng cáo
Để tìm kiếm được điểm (tham số m) thỏa mãn nhu cầu Đk T ta cần sử dụng những công thức sau:
+ Khoảng cách từ điểm M(x0; y0) đến đường thẳng d: ax + by + c = 0 là:
d(M; d) =
+ Khoảng cách hai điểm A(xA; yA) và B ( xB; yB) là:
AB =
+ Để điểm M (x0; y0) cách đều hai tuyến phố thẳng d: ax + by + c = 0 và d’: a’x + b’y + c’ = 0
⇔ d( M;d) = d( M;d’) ⇔
+ Tam giác ABC cân tại A khi và chỉ khi AB = AC.
Ví dụ 1. Cho d:
Tìm điểm M trên d cách A(0; 1) một đoạn bằng 5
A. M(
;
)
B. M1(4; 4) ; M2(
;
)
C. M1(4; 4) ; M2(-
; –
)
D. M( 2; -3)
Lời giải
Lấy điểm M( 2 + 2t; 3 + t) nằm trên d ; AM→( 2 + 2t; t + 2)
Để AM = 5 khi và chỉ khi
(2t + 2)2 + (t + 2)2 = 25 hay 5t2 + 12t – 17 = 0
Suy ra t = 1 hoặc t = –
+ Với t = 1 thì M( 4; 4)
+ Với t = –
⇒ M2(-
; –
).
Chọn C
Quảng cáo
Ví dụ 2. Khoảng cách nhỏ nhất từ điểm M(15; 1) đến một điểm bất kì thuộc đường thẳng ∆ :
bằng:
A. √10
B. 

Lời giải
+ Ta đưa đường thẳng ∆ về dạng tổng quát:
∆:
⇒ ( ∆) : 1(x – 2) – 3( y – 0) = 0 hay x – 3y – 2 = 0
+ Với mọi điểm N bất kì thuộc ∆ ta luôn có: MN ≤ d( M; ∆)
⇒ MNmin = d( M; ∆) =
= √10
Chọn A.
Ví dụ 3. Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A( -2; 2), B(4; -6) và đường thẳng . Tìm điểm M thuộc
d:
sao cho M cách đều hai điểm A; B
A. M( 3; 7)
B. M( -3; -5)
C. M( 2; 5)
D. M( -2; -5)
Lời giải
Do điểmM thuộc đường thẳng d nên tọa độ M( t; 1 + 2t)
MA2 = ( t + 2)2 + ( 2t – 1)2 và MB2 = (t – 4)2 + (2t + 7)2
Để MA = MB ⇔ AM2 = MB2
⇔ ( t + 2)2 + (2t – 1)2 = (t – 4)2 + (2t + 7)2
⇔ t2 + 4t + 4 + 4t2 – 4t + 1 = t2 – 8t + 16 + 4t2 + 28t + 49
⇔ 20t = – 60 ⇔ t = -3
⇒ Tọa độ điểm M ( -3; -5).
Chọn B.
Ví dụ 4. Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(-1; 2) ; B(-3;2) và đường thẳng d:
2x – y + 3 = 0. Tìm điểm C thuộc d sao cho tam giác ABC cân tại C.
A. C( -2; -1)
B. C( 1; -2)
C. C( -1; 1)
D. C(0; 3)
Lời giải
Gọi tọa độ điểm C(x;y) .
+ Do điểm C thuộc đường thẳng d nên 2x – y + 3 = 0 ( 1) .
+ Ta có AC2 = ( x + 1)2 + ( y – 2)2 và BC2 = ( x + 3)2 + (y – 2)2
Để tam giác ABC cân tại C thì CA = CB ⇔ CA2 = CB2
⇔ ( x + 1)2 + (y – 2)2 = (x + 3)2 + (y – 2)2
⇔ x2 + 2x + 1 + y2 – 4y + 4 = x2 + 6x + 9 + y2 – 4y + 4
⇔ – 4x = 8 (2).
Từ( 1) và ( 2) ta có hệ phương trình :
Vậy tọa độ điểm C(-2; -1).
Chọn A.
Quảng cáo
Ví dụ 5. Tìm toàn bộ những giá trị của tham số m để khoảng chừng cách từ điểm A(-1;2) đến đường thẳng
∆: mx + y – m + 4 = 0 bằng 2√5 .
A. m = 2
B. m = -2 hoặc m = 
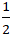
Lời giải
Khoảng cách từ A đến đường thẳng ∆:
d(A; Δ) =
= 2√5
⇔ |- 2m + 6| = 2√5.
⇔ |m – 3| = √5.
⇔ 4m2 + 6m – 4 = 0
⇔ m = -2 hoặc m =
Chọn B.
Ví dụ 6. Tìm toàn bộ những giá trị của tham số m để khoảng chừng cách từ giao điểm của hai tuyến phố thẳng
d1:
và d2: x – 2y + m = 0 đến gốc toạ độ bằng 2.
A. m = -4 hoặc m = 2
B. m = – 4 hoặc m = -2
C. m = 4 hoặc m = 2
D. m = 4 hoặc m = -2
Lời giải
+ ta đưa đường thẳng d1 về dạng tổng quát:
(d1 ):
⇒ phương trình d1: 1( x – 0) + 1 (y – 2) = 0 hay x + y – 2 = 0
+ Giao điểm của d1 và d2 là nghiệm hệ phương trình:
Vậy giao điểm của hai tuyến phố thẳng d1 và d2 là M(4 – m; m – 2)
+ Khi đó: OM = 2 ⇔ OM2 = 4
⇔(4 – m)2 + (m – 2)2 = 4 ⇔ 16 – 8m + mét vuông + mét vuông – 4m + 4 = 4
⇔2m2 – 12m + 16 = 0 ⇔ m = 2 hoặc m = 4
Chọn C.
Ví dụ 7. Với giá trị nào của m thì đường thẳng Δ:
x –
y + m = 0 tiếp xúc với đường tròn
( C): tâm O(0; 0) và bán kính R = 1?
A. m = ±1
B. m = 0
C. m = √2
D. m =
Lời giải
Để đường thẳng ∆ tiếp xúc đường tròn khi và chỉ khi khoảng chừng cách từ tâm đường tròn đến đường thẳng ∆ bằng bán kính R
d(O; Δ) = R ⇔
= 1 ⇔ m = ±1.
Chọn A.
Ví dụ 8: Tìm điểm M trên trục Ox sao cho nó cách đều hai tuyến phố thẳng:
d1: 3x + 2y – 6 = 0
và d2: 3x + 2y + 6 = 0 ?
A. (1; 0)
B. (0; 0)
C. (0; √2)
D. (√2; 0)
Hướng dẫn giải
Gọi tọa độ điểm M( a;0) .
Khoảng cách từ M đến hai tuyến phố thẳng là:
d(M; d1) =
và d( M; d2) =
để M cách đều hai tuyến phố thẳng khi và chỉ khi :
=
⇒ Tọa độ điểm M ( 0; 0)
Chọn B.
Ví dụ 9: Cho hai điểm A( 1; 2) và B( 4; 6). Tìm tọa độ điểm M trên trục Oy sao cho diện tích s quy hoạnh
tam giác MAB bằng 1 ?
A. (0 ;
) và (0;
)
B. (1; 0)
C. (4; 0)
D. Đáp án khác
Hướng dẫn giải
+ Độ dài đoạn AB =
= 5
+ Điểm M thuộc Oy nên tọa độ M ( 0; y).
+ Vì diện tích s quy hoạnh tam giác MAB bằng 1 nên S =
AB.d( M;AB) = 1
⇔
.5.d( M; AB) = 1 ⇒ d( M; AB) =
+ Phương trình đường thẳng AB:
⇒ Phương trình AB: 4( x – 1) – 3( y – 2) = 0 hay 4x – 3y + 2 = 0
⇒ d( M; AB) =
=
Vậy có hai điểm M thỏa mãn nhu cầu M(0; 0) hoặc M( 0;
)
Chọn D.
Ví dụ 10 : Cho ba điểm A(0; 1) ; B(12; 5) và C(-3; 0). Đường thẳng nào sau này cách đều ba điểm
A; B; C
A. x – 3y + 4 = 0
B. –x + y + 10 = 0
C. x + y = 0
D. 5x – y + 1 = 0.
Lời giải
Cách 1 : Ta có : AB→( 12; 4); AC→( -3; -1) ⇒ AB→ = – 4AC→
⇒ ba điểm A ; B và C thẳng hàng .
⇒ Nếu đường thẳng d cách đều 3 điểm A, B ; C thì nó phải tuy nhiên tuy nhiên hoặc trùng với AB.
Đường thẳng (d) nhận vecto AC→( -3 ; -1) làm VTCP nên nhận vecto n→( 1 ; -3) làm VTPT
⇒ đường thẳng d có dạng : x – 3y + c = 0
Kiểm tra những phương án, ta thấy phương án A thỏa mãn nhu cầu
Cách 2: Tính khoảng chừng cách từ 3 điểm đến lần lượt những đường thẳng trong những phương án A, B, C, D.
Chọn A.
Ví dụ 11. Cho A(2; 2) ; B(5; 1) và đường thẳng ∆: x – 2y + 8 = 0 . Điểm C thuộc ∆ và C có
hoành độ dương sao cho diện tích s quy hoạnh tam giác ABC bằng 17. Tọa độ của C là
A. (10; 12)
B. (12 ; 10)
C. ( 8; 8)
D. (10; 8)
Lời giải
Phương trình đường thẳng AB:
⇒ ( AB) : 1(x – 2) + 3(y – 2) = 0 hay x + 3y – 8 = 0
Điểm
Độ dài AB =
= √10 và khoảng chừng cách từ C đến AB:
D( C; AB)=
=
Diện tích tam giác ABC là:
S =
AB.d(C; AB) = 17 ⇔
√10.
= 17
⇔ |5t – 16| = 34 ⇒
Mà C có hoành độ dương nên t = 10 ⇒ C( 12; 10) .
Chọn B.
Câu 1: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(1;1) ; B( -2; 4) và đường thẳng
∆: mx – y + 3 = 0. Tìm toàn bộ những giá trị của tham số m để ∆ cách đều hai điểm A; B.
A. m = 1 hoặc m = -2
B. m = -1 hoặc m = 2
C. m = 1 hoặc m = -1
D. m = 2 hoặc m = – 2
Hiển thị lời giải
Đáp án: C
Trả lời:
+ Để một đường thẳng ∆ cách đều hai điểm A và B thì ∆ // AB hoặc ∆ là đường trung trực của đoạn thẳng AB.
+ Gọi d là đường thẳng tuy nhiên tuy nhiên với AB ⇒ d nhận AB→( -3; 3) VTCP nên nhận
n→( 1; 1) làm VTPT
⇒ (d) có dạng : x + y + c = 0
Để d// ∆ ⇔ m/1= (-1)/1≠3/c ⇔ m= -1 và c ≠-3.
⇒ Với m = – 1 thì d//∆ nên ∆ cách đều hai điểm A và B
+ Gọi ( d’) là đường trung trực của đoạn AB.
( d’) :
⇒ Phương trình ( d’) : 1( x +
) – 1( y –
) = 0 hay x – y + 3 = 0
⇒ Để d’ trùng với ∆ thì m = 1. Khi đó; ∆ là đường trùng trực của AB nên ∆ cách đều hai điểm A và B.
Vậy với m = 1 hoặc m = -1 thì đường thẳng ∆ cách đều hai điểm A và B
Câu 2: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A( 1; 1) ; B(4; – 3) và đường thẳng
d: x – 2y – 1 = 0. Tìm điểm M thuộc d có tọa độ nguyên và thỏa mãn nhu cầu khoảng chừng cách từ M đến đường thẳng AB bằng 6.
A. M( 3; 7)
B. M( 7; 3)
C. M( -43; -27)
D. M(3; –
)
Hiển thị lời giải
Đáp án: B
Trả lời:
+ Phương trình đường thẳng AB:
⇒ ( AB) : 4(x – 1) + 3(y – 1) = 0 hay 4x + 3y – 7 = 0
+ Lấy điểm M ( 2m + 1; m) thuộc d với m nguyên
Khi đó để khoảng chừng cách từ M đến AB bằng 6 thì:
6 = d(M; AB) =
⇔|11m – 3| = 30 ⇔
→ M(7;3).
Câu 3: Trong mặt phẳng với hệ tọa độ oxy , cho điểm A( 0; 1) và đường thẳng
d:
. Tìm điểm M thuộc d và cách A một khoảng chừng bằng 5, biết M có hoành độ âm.
A. M(-2; 1)
B. 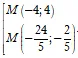
; –
)
D. M( -4; 4)
Hiển thị lời giải
Đáp án: C
Trả lời:
Do điểm M thuộc đường thẳng d nên tọa độ của M( 2 + 2t; 3 + t)
với 2 + 2t < 0 hay t < -1 vì M có hoành độ âm
Khi đó để M cách A một khoảng chừng bằng 5 thì AM = 5 ⇔ AM2 = 25
⇔( 2 + 2t)2 + (2 + t)2 = 25 ⇔ 4 + 8t + 4t2 + 4 + 4t + t2 = 25
⇔5t2 + 12t – 17 = 0
⇔
Với t =
thì M(-
; –
)
Câu 4: Biết rằng có đúng hai điểm thuộc trục hoành và cách đường thẳng
∆: 2x – y + 5 = 0
một khoảng chừng bằng 2√5. Tích hoành độ của hai điểm đó bằng:
A. – 


Hiển thị lời giải
Đáp án: A
Trả lời:
Điểm M ( x; 0) thuộc trục hoành.
Do khoảng chừng cách từ M đến ∆ là 2√5 nên
d(M; Δ) = 2√5 ⇔
⇔ |2x + 5| = 10
⇔
Vậy có hai điểm thỏa mãn nhu cầu là M1(
; 0) và M2(
; 0).
Tích hoành độ của hai điểm đó là:
.
= –
Câu 5: Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A(3; -1) và B(0;3). Tìm điểm M thuộc trục hoành sao cho khoảng chừng cách từ M đến đường thẳng AB bằng 1.
A. M(
; 0) ; M(1;0)
B. M(
; 0) ;M(
; 0)
C. M( –
; 0) ;M( -1; 0)
D. M( –
; 0) ;M( –
; 0)
Hiển thị lời giải
Đáp án: A
Trả lời:
Phương trình ( AB):
⇒ ( AB) : 4( x – 3) + 3( y + 1) = 0 hay 4x + 3y – 9 = 0
Gọi điểm M thuộc trục hoành có tọa độ là ( x; 0) .
Để khoảng chừng cách từ M đến AB bằng 1 thì:
1 = d( M; AB) =
⇔|4x – 9| = 5
⇔
Câu 6: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(3; 0) và B( 0; -4) .
Tìm điểm M thuộc trục tung sao cho diện tích s quy hoạnh tam giác MAB bằng 6
A. M(0; 0) hoặc M(0; -8)
B. M(0; – 8)
C. M(6; 0)
D. M(0; 0)
Hiển thị lời giải
Đáp án: A
Trả lời:
+ Phương trình AB theo đoạn chắn :
= 1 hay -4x + 3y + 12 = 0
+ AB =
= 5
+ Gọi điểm M( 0; y) thuộc trục tung.
⇒ khoảng chừng cách từ M đến AB là d( M; AB) =
Để diện tích s quy hoạnh tam giác MAB là 6 thì:
S =
.AB.d( M; AB) = 6 ⇔
.5.
= 6
⇔ |3y + 12| = 12 ⇒
Vậy có hai điểm M thỏa mãn nhu cầu là M(0; 0 ) hoặc M ( 0; -8)
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho hai tuyến phố thẳng (a): 3x – 2y – 6 = 0 và
(b) : 3x – 2y + 12 = 0. Tìm điểm M thuộc trục hoành sao cho M cách đều hai tuyến phố thẳng đã cho.
A. M( -2; 0)
B. M(-1; 0)
C. M(1; 0)
D. M(0; 0)
Hiển thị lời giải
Đáp án: B
Trả lời:
D0 M thuộc trục hoành nên tọa độ M (x; 0)
Khoảng cách từ M đến hai đường thẳng là:
d( M; a) =
và d( M; b) =
Để điểm M cách đều hai tuyến phố thẳng a và b thì:
=
⇔ |3x – 6| = |3x + 12|
⇔3x – 6 = – 3x – 12 ⇔x = -1
⇒ Điểm M ( -1; 0) .
Câu 8: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(1; 2) ; B( 0; 3) và đường thẳng
d: y = 2. Tìm điểm C thuộc d sao cho tam giác ABC cân tại B
A. C(1; 2)
B. C(4; 2)
C. C(1; 2) hoặc C( -1; 2)
D. C(-1; 2)
Hiển thị lời giải
Đáp án: C
Trả lời:
Gọi toạ độ của điểm C( x; y) .
Do C thuộc d nên y = 2. (1)
Ta có: BA2 = (1 – 0)2 + (2 – 3)2 = 2 và BC2 = x2 + (y – 3)2
Để tạm giác ABC cân tại B thì BA = BC ⇔ BA2 = BC2
⇔ 2 = x2 + (y – 3)2 (2)
Từ ( 1) và (2) ta có hệ phương trình :
⇒ Có hai điểm C thỏa mãn nhu cầu đầu bài là C( 1; 2) hoặc C( -1; 2)
Câu 9: Phương trình của đường thẳng qua P(2; 5) và cách Q.(5; 1) một khoảng chừng bằng 3 là:
A. 7x + 24y – 13 = 0 .
B. x = 2
C. x = 2 hoặc 7x + 24y – 134 = 0 .
D. 3x + 4y – 5 = 0
Hiển thị lời giải
Đáp án: C
Trả lời:
+ Đường thẳng ∆ qua P( 2; 5) và có VTPT n→( a; b) .
⇒ Phương trình ∆: a(x – 2) + b(y – 5) = 0 hay ax + by – 2a – 5b = 0
+ Khoảng cách từ điểm Q. đến ∆:
d(Q., ∆) = 3 ⇔
= 3 ⇔ |3a – 4b| = 3.
⇔ -24ab + 7b2 = 0 ⇔
+ Với b = 0, chọn a = 1 thì phương trình ∆ : x – 2 = 0.
+ Với b =
a , chọn a = 7⇒ b = 24 phương trình ∆ : 7x + 24y – 134 = 0
Câu 10: Cho hai điểm A(3; -1) và B(0; 3) . Tìm tọa độ điểm M trên trục Ox sao cho khoảng chừng cách từ
M đến đường thẳng AB bằng AB?
A. ( -4; 0); (-3,5; 0)
B. (2; 0) và (1; 0)
C. (4; 0)
D. (-4; 0) ; ( 8,5; 0)
Hiển thị lời giải
Đáp án: D
Trả lời:
+ Ta gọi tọa độ điểm M nằm trên trục Ox là M( a ; 0)
+ Phương trình đường thẳng AB :
⇒ Phương trình AB : 4(x – 3) + 3(y + 1) = 0 hay 4x + 3y – 9 = 0
+ Độ dài đoạn AB =
= 5
+ Để khoảng chừng cách từ M đến đường thẳng AB bằng AB thì d( M; AB) = 5
⇔
= 5 ⇔|4a – 9| = 25
⇔
Vậy có hai điểm M thỏa mãn nhu cầu là M ( 8,5; 0) và M( -4; 0) .
Câu 11: Cho hai điểm A( 2; 3) và B(1; 4). Đường thẳng nào sau này cách đều hai điểm A; B?
A. x – y + 2 = 0
B. x – y + 100 = 0
C. x + 2y = 0
D. 2x – y + 10 = 0.
Hiển thị lời giải
Đáp án: A
Trả lời:
Cách 1: Gọi d là đường thẳng cách đều 2 điểm A và B ta có:
M(x; y) ∈ d ⇔ MA = MB ⇔ MA2 = MB2
⇔ (x – 2)2 + (y – 3)2 = ( x – 1)2 + (y – 4)2
⇔ x2 – 4x + 4 + y2 – 6y + 9 = x2 – 2x + 1 + y2 – 8y + 16
⇔2x – 2y + 4 = 0 hay x – y + 2 = 0
Cách 2: Gọi I là trung điểm của đoạn AB ⇒ I(
;
)
Gọi d là đường thẳng cách đều 2 điểm A và B suy ra d là đường trung trực của đoạn AB hoặc d// AB.
+ Viết đường trung trực d của AB :
⇒ d trải qua I(
;
) và nhận AB→( -1; 1) làm VTPT
⇒ d: -(x –
) + (y –
) = 0 ⇒ d: -x + y – 2 = 0
+ Viết đường thẳng d’ tuy nhiên tuy nhiên với AB.
⇒ d’ nhận AB→( -1 ;1) làm VTCP và VTPT là n→(1 ; 1)
⇒ (d’) có dạng 😡 + y + c = 0.
Trong những phương án chỉ có phương án A thỏa mãn nhu cầu.
Câu 12: Tìm tọa độ điểm M nằm trên trục Ox và cách đều 2 đường thẳng
(a): 2x – 3y + 4 = 0 và (b): 2x + 3y + 2 = 0
A. (
; 0)
B. (
; 0)
C. (1; 0)
D. ( –
; 0)
Hiển thị lời giải
Đáp án: D
Trả lời:
Điểm M nằm trên trục Ox nên tọa độ điểm M ( a ; 0) .
Khoảng cách từ M đến hai tuyến phố thẳng là :
d(M ; a) =
và d(M ; b) =
Để M cách đều hai tuyến phố thẳng (a) và (b) khi và chỉ khi :
=
⇔ |2a + 4|= |2a + 2| ⇔
⇒ Điểm M( –
; 0)
Chuyên đề Toán 10: khá đầy đủ lý thuyết và những dạng bài tập có đáp án khác:
Giới thiệu kênh Youtube Tôi
Trang trước
Trang sau
Viết phương trình tiếp tuyến của đồ thị hàm số lúc biết thông số góc
Trang trước
Trang sau
Quảng cáo
*Ý nghĩa hình học của đạo hàm:
Đạo hàm của hàm số y= f(x) tại điểm x0 là thông số góc của tiếp tuyến với đồ thị (C) của hàm số tại điểm M0(x0; f(x0) ).
Khi đó phương trình tiếp tuyến của (C) tại điểm M0 là:
y–y0=f’ (x0).(x–x0)
1.- Gọi ∆ là tiếp tuyến cần tìm có thông số góc k.
– Giả sử M(x0 ; y0) là tiếp điểm. Khi đó x0 thỏa mãn nhu cầu: f’(x0)= k (*) .
– Giải (*) tìm x0. Suy ra y0= f(x0). Phương trình tiếp tuyến cần tìm là: y= k(x- x0) + y0
2. Cho đường thẳng d : y= kdx + b
+) Nếu ∆ // d thì k∆ = kd
+) Nếu ∆ vuông góc với d thì : k∆. kd = -1 ⇔ k∆ = (- 1)/kd
Ví dụ 1 : Viết phương trình tiếp tuyến của đồ thị (C) :y=-x4-x2+6, biết tiếp tuyến vuông góc với đường thẳng d:y=1/6x-1 .
A.y= 6x+ 1 B. y= – 6x+ 6 C.y= -6x+ 10 D. y= 6x+ 12
Hướng dẫn giải
Hàm số đã cho xác lập D=R.
Đạo hàm của hàm số: y’= – 4×3 – 2x
Gọi ∆ là tiếp tuyến của đồ thị (C) của hàm số và ∆ vuông góc với đường thẳng d : y=1/6x-1 .
⇒ đường thẳng ∆ có thông số góc : k= -6.
Cách 1: Gọi M(x0 ; y0) là tọa độ tiếp điểm của tiếp tuyến ∆ và đồ thị (C) của hàm số .
Khi đó, ta có phương trình: y'(x0)=-6 ⇔-4×03-2×0=-6
⇔(x0-1)(2×02+2×0+3)=0(*).
Vì 2×02+2×0+3 > 0,∀x0∈R nên phương trình ( *) tương đường x0 =1
⇒ y0= y(1)= 4 nên M( 1 ; 4)
Phương trình tiếp tuyến cần tìm là: y=-6(x-1)+4=-6x+10.
Cách 2: Phương trình tiếp tuyến ∆ có dạng y=-6x+m ( **)
Do ∆ tiếp xúc (C) tại điểm M(x0 ; y0) khi hệ phương trình sau có nghiệm x0 :
Thay vào (**) ta có phương trình tiếp tuyến là: y= – 6x+ 10
Chọn C.
Quảng cáo
Ví dụ 2. Cho hàm số y=1/3 x3-x+2/3 có đồ thị là (C). Tìm trên đồ thị (C) điểm mà tại đó tiếp. tuyến của đồ thị vuông góc với đường thẳng d: y=-1/3 x+2/3.
A. ( 1; -2) và ( -2; 0) B. ( – 2; 0) và ( 2; 4/3 )
C. ( -2; 5) và ( 1;0) D. Đáp án khác
Hướng dẫn giải
Hàm số đã cho xác lập D= R.
Ta có đạo hàm: y’=x2-1
GọiM(x0;y0)∈(C) ⇔y0=1/3 x03-x0+2/3,
Tiếp. tuyến ∆ tại điểm M có hệ số góc: y'(x0)=x02-1
Đường thẳng d: có hệ số góc k2=-1/3
Ví dụ 3: Trong những tiếp tuyến tại những điểm trên đồ thị hàm số y=x3-3×2+2, tiếp tuyến có thông số góc nhỏ nhất bằng
A.-3 B.3 C.4 D.0
Hướng dẫn giải
Đạo hàm:y’=3×2-6x=3(x-1)2 -3 ≥-3với mọi x.
Vậy trong những tiếp tuyến tại những điểm trên đồ thị hàm số đã cho, tiếp tuyến có thông số góc nhỏ nhất bằng – 3.
Chọn A.
Ví dụ 4: Cho hàm số y= x3+ 3×2- 9x+ 5 có đồ thị (C). Trong toàn bộ những tiếp tuyến của đồ thị (C), hãy tìm tiếp tuyến có thông số góc nhỏ nhất.
A: y=-2x+4 B: x+y+12=0 C: 12x+y-4=0 D: x-12y+4=0
Hướng dẫn giải
Ta có đạo hàm : y’= 3×2+ 6x- 9
Gọi x0 là hoành độ tiếp điểm của tiếp tuyến, vậy f’ (x0 )= 3.×02+6×0-9
Ta có: 3.×02+6×0-9=3( x02+2×0+1)-12=3(x0+1)2-12 ≥ -12 ∀x0
Vậy min f’ (x0 )=-12 tại x0= -1 ⇒ y0= 16
Suy ra phương trình tiếp tuyến cần tìm:y= -12(x+1)+16 hay y=-12x+4
Chọn C
Ví dụ 5.Cho hàm số y= x3+ 3mx2+ (m+ 1)x+ 1 ( 1), m là tham số thực. Tìm những giá trị của m để tiếp tuyến của đồ thị của hàm số (1) tại điểm có hoành độ x=-1 trải qua điểm A(1;2).
A: 1 B: -1 C: 3 D: 5/8
Quảng cáo
Hướng dẫn giải
Ta có đạo hàm: y’= 3×2+ 6mx + m+ 1
Với x0 = – 1 ⇒ y0= 2m- 1 và y’( -1) = – 5m+ 4.
Phương trình tiếp tuyến tại điểm M(-1;2m-1):
y=(-5m+4)(x+1)+2m-1 (d).
Ta có điểm A( 1; 2) thuộc đường thẳng d nên:
2= ( – 5m+ 4).(1+1) +2m- 1 ⇔ 2= – 10m+ 8+ 2m- 1
⇔ – 8m+ 5= 0 ⇔ m= 5/8.
Chọn D.
Ví dụ 6:Cho hàm số y= -x3- 3×2+ 9x – 5 (C). Trong toàn bộ những tiếp tuyến của đồ thị (C) hãy tìm tiếp tuyến có thông số góc lớn số 1.
A: y=8x-3 B: y=6x-4 C: y=10x-2 D: y=12x-4
Hướng dẫn giải
Ta có đạo hàm: y’= – 3×2- 6x+ 9
Gọi x0 là hoành độ tiếp điểm của tiếp tuyến, ta có y’ (x0 )= -3×02-6×0+9
Từ đó suy ra max y’ (x0)=12 tại x0= – 1.
Với x0= -1 ⇒ y0= – 16 , phương trình tiếp tuyến cần tìm:y=12x-4
Chọn D
Ví dụ 7: Cho hàm số y= (2x-1)/(x-1) có đồ thị ( C) . Gọi I(1;2) Tìm điểm M thuộc (C) sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng IM?
A. M(3;2) B. (0;1) C. (2;3) D. Cả B và C đúng
Hướng dẫn giải
Ví dụ 8:Cho hàm số y= 2x/x+1. Có mấy điểm M thuộc C, biết tiếp tuyến của (C) tại M cắt hai trục tọa độ tại A; B và tam giác 0AB có diện tích s quy hoạnh bằng 1/4
A: 0 B: 1 C: 2 D: 3
Hướng dẫn giải
Ví dụ 9. Cho đồ thị (C): y= (( 3m+1)x-m)/(x+m).Tìm m để tiếp tuyến tại giao điểm của (C) với Ox tuy nhiên tuy nhiên với đường thẳng d: y=-x-5.
A. (- 1)/6; (- 1)/2 B: – 1/4 C: -1/2 ; 1 D: Tất cả sai
Hướng dẫn giải
Ví dụ 10: Gọi (C) là đồ thị của hàm số y=1/3×3 -m/2×2+1/3 (m là tham số).
Gọi M là yếu tố thuộc (C) có hoành độ bằng -1. Tìm m để tiếp tuyến của (C) tại điểm M tuy nhiên tuy nhiên với đường thẳng 5x-y=0
A: m=1 B: m=2 C: m=3 D: m=4
Hướng dẫn giải
Ví dụ 11. Viết phương trình tiếp tuyến d với đồ thị (C): y= x3- 3×2+ 2, biết d cắt những trục Ox; Oy lần lượt tại A; B thỏa mãn nhu cầu OB= 9OA.
A. y= 9x+ 5 và y= 9x- 25 B. y= 9x+ 7 và y= 9x- 25
C. y= – 9x+ 1 và y= 9x + 7 D. Đáp án khác
Hướng dẫn giải
Gọi M(x0; y0) là toạ độ tiếp điểm
Đạo hàm của hàm số đã cho: y’= 3×2- 6x
Theo bài toán, đường thẳng d ≡AB.
Ví dụ 12. Cho hàm số y=x3-2×2+8x+5 có đồ thị là (C). Khẳng định nào sau này đúng nhất ?
A. Không có bất kỳ hai tiếp tuyến nào của đồ thị hàm số lại vuông góc với nhau
B. Luôn có bất kỳ hai tiếp tuyến nào của đồ thị hàm số lại vuông góc với nhau
C. Hàm số trải qua điểm M( 1 ;17)
D. Cả A, B, C đều sai
Hướng dẫn giải
Ta có y'(x)=3×2-4x+8
Xét phương án A:
Giả sử trái lại sở hữu hai tiếp tuyến với đồ thị vuông góc với nhau.
Gọi x1; x2 tương ứng là những hoành độ của hai tiếp điểm của hai tiếp tuyến đó.
Gọi k1 ; k2 lần lượt là những thông số góc của hai tiếp tuyến tại những điểm trên (C) có hoành độ x1 ; x2 .
Khi đó k1,k2=-1⇒y’ (x1 ).y’ (x2 )=-1
⇒(3×12-4×1+8)(3×22-4×2+8)=-1
Tam thức f(t)=3t2-4t+8 có nên f(t)> 0∀t∈R
⇒ ( 1) không thể xẩy ra.
Vậy, giả thiết phản chứng là sai. Không có bất kỳ hai tiếp tuyến nào của đồ thị hàm số lại vuông góc với nhau
Chọn A.
Ví dụ 13.Cho hàm số: y= 2x+2/x-1 có đồ thị ( C). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến có thông số góc bằng -1.
A. y= -x- 2; y= -x+ 7. B. y= -x- 5; y= -x+ 6.
C. y= -x- 1; y= -x+ 4. D. y= -x- 1; y= -x+ 7.
Hướng dẫn giải
Ví dụ 14. Viết phương trình tiếp tuyến với đồ thị hàm số: y=2x/(x-1) nếu tiếp tuyến vuông góc với đường thẳng (Δ):9x-2y+1=0
Hướng dẫn giải
Ví dụ 15: Cho hàm số y=x4/4+x2/2+2 có đồ thị (C). Viết phương trình tiếp tuyến ∆ của (C) tuy nhiên tuy nhiên với đường thẳng d: y= 2x- 2
Hướng dẫn giải
Đạo hàm y’= x3+ x
Đường thẳng d có thông số góc k= 2.
Do tiếp tuyến ∆ của (C) tuy nhiên tuy nhiên với đường thẳng d:y= 2x-2 nên thông số góc của đường thẳng ∆ là k∆= 2
⇒ x3+ x= 2 ⇒ x= 1
Tại x= 1 ta có y= 11/4;y’ (1)=2
Phương trình tiếp tuyến ∆: y=2(x-1)+11/4=2x+3/4
Chọn A
Ví dụ 16: .Cho hàm số y=2×4-4×2-1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến vuông góc với đường thẳng x- 48y + 1= 0..
Hướng dẫn giải
Ta có đạo hàm: y’=8×3-8x.
Gọi M(x0.y0 )Tiếp tuyến tại M có phương trình:.
y=(8×03-8×0)(x-x0)+2×04-4×02-1..
Vì tiếp tuyến vuông góc với đường thẳng x-48y+1=0 hay y= 1/48 x+ 1/48.
Nên ta có: y'(x0).1/48=-1⇔y'(x0)=-48.
8×03-8×0+48=0 ⇒x0=-2 ⇒y0=15..
Phương trình Δ:y=-48(x+2)+15=-48x-81.
Chọn A.
Ví dụ 17: Tìm m để đồ thị hàm số y=1/3 mx3+(m-1)x2+(2-3m)x+1 tồn tại đúng điểm có hoành độ dương mà tiếp tuyến tại đó vuông góc với đường thẳng d: x+ 2y – 3= 0.
Hướng dẫn giải
Hàm số đã cho xác lập trên R.
Ta có: y’=mx2+2(m-1)x+2-3m.
Ví dụ 18Gọi (Cm) là đồ thị của hàm số y=1/3×3 +m/2×2+1/3 (m là tham số)
.
Gọi M là yếu tố thuộc (Cm) có hoành độ bằng -1. Tìm m để tiếp tuyến của (Cm) tại điểm M tuy nhiên tuy nhiên với đường thẳng 5x-y=0
A: m=1 B: m=2 C: m=3 D: m=4
Hướng dẫn giải
Câu 1: Biết rằng trên đồ thị (C): y=x3-(m+1)x2+(4m+2)x+1 tồn tại đúng 1 điểm mà từ đó kẻ được tiếp tuyến vuông góc với đường thẳng d: x+ 10y+ 2013= 0.Viết phương trình tiếp tuyến của (C) tại điểm đó
A. y= – 3x+ 4 B. y= 6x- 9
C. y= 10x – 9 D. y= – 8x+ 12
Hiển thị lời giải
+ Đạo hàm của hàm số đã cho là: y’= 3×2 – 2( m+ 1)x + 4m+ 2
+ Gọi tiếp điểm là M( a; b), tiếp tuyến tại M có thông số góc là:
k2=y'(a)=3a2-2(m+1)a+4m+2 ( 1)
Do tiếp tuyến cần tìm vuông góc với đường thẳng d: x+ 10y+ 2013 = 0 nên :
k1. k2 = -1 ⇒ k2 = 10 ( 2)
Từ (1) và (2)suy ra: 3a2-2(m+1)a+4m+2=10
⇔ 3a2-2(m+1)a+4m-8=0 (*)
Trên đồ thị ( C) chỉ có đúng một điểm mà tiếp tuyến tại đó vuông góc với đường thẳng d nên (*) có nghiệm kép hay
⇔ ( m+ 1)2 – 3( 4m- 8) = 0 ⇔ mét vuông+2m+ 1 – 12m + 24 = 0
⇔ mét vuông – 10m + 25 = 0 ⇔ m= 5
thay vào (*) ta được a = 2 ⇔ M( 2; 29) .
Vậy, tiếp tuyến cần tìm là y= 10x+ 9
Chọn C.
Câu 2: Cho hàm số y= x3- 3x + 1 (C). Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến vuông góc với trục Oy.
A. y= 2;y= -1 B, y= 3; y= – 1 C. y= 3;y= -2 D. x= 3; x= – 1
Hiển thị lời giải
Ta có đạo hàm y’= 3×2- 3. Gọi M( x0; y0) là tiếp điểm.
Vì tiếp tuyến vuông góc với Oy nên tiếp tuyến có dạng y+ c= 0
⇒ y’ (x0 )=0 ⇔ 3×02-3=0 ⇒ x0= ±1
+ Với x0= 1 ta có y0= – 1 nên phương trình tiếp tuyến tại điểm (1; -1) là
y+ 1= 0 (x – 1) hay y= -1
+ Với x0= – 1 ta có yo= 3 nên phương trình tiếp tuyến tại điểm ( -1; 3) là :
y- 3= 0( x+ 1) hay y= 3
Từ đó ta tìm kiếm được hai tiếp tuyến là y= 3 và y= -1
Chọn B.
Câu 3: Cho đồ thị hàm số ( C); y= (2x+2)/(x-1). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến tạo với hai trục tọa độ một tam giác vuông cân
Hiển thị lời giải
Hàm số xác lập với mọi x≠1. Ta có đạo hàm: y’=(-4)/(x-1)2 <0 với mọi x.
Gọi M( x0; y0) là tiếp điểm, suy ra phương trình tiếp tuyến của (C).
Vì tiếp tuyến tạo với hai trục tọa độ một tam giác vuông cân
⇒ tiếp tuyến phải vuông góc với một trong hai tuyến phố phân giác y= ±x, do đó thông số góc của tiếp tuyến bằng 1 hoặc – 1.
Mà y’< 0 nên ta có:
Câu 4: Cho hàm số y=3x-2/x-2 Viết phương trình tiếp tuyến d với đồ thị hàm số biết d tạo với trục hoành một góc
Hiển thị lời giải
Câu 5: Cho hàm số y=((3m+1)x-mét vuông+m)/(x+m)có đồ thị là ( C); .Với giá trị nào của m thì tại giao điểm đồ thị với trục hoành, tiếp tuyến của đồ thị sẽ tuy nhiên tuy nhiên với đường thẳng d: x – y- 10 = 0.
Hiển thị lời giải
Câu 6: Cho hàm số y=x3-2×2+2x” ” có đồ thị (C). Gọi x1; x2 là hoành độ những điểm M; N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y=-x+2022. Khi đó x1+ x2 bằng:
Hiển thị lời giải
Ta có:3×2 -4x+2 .
Tiếp tuyến tại M; N của (C) vuông góc với đường thẳng y= -x+ 2022.
Nên tiếp. tuyến tại M và N có hệ số góc là 1
Hoành độ x1; x2 của những điểm M; N là nghiệm của phương trình: 3×2-4x+2=1.
Suy ra ( hệ thức Vi-et).
Chọn A.
Câu 7: Cho đường cong(C):y=(3x+1)/(1-x). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến tuy nhiên tuy nhiên với đường thẳng (d): x-4y-21=0.
A: y= -x-1/4 B: 2y+4x-1=0 C: x-4y-5=0 D: Đáp. án khác
Hiển thị lời giải
Câu 8: Cho hàm số y=f(x)=(x2-x+2)/(x-1)(C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có thông số góc k=1.
A: y+x-6=0 B: x-y+6=0 C: -x+y+6=0 D:không có đường thẳng nào
Hiển thị lời giải
Câu 9: Tìm m để tiếp tuyến có thông số góc nhỏ nhất của ( C) : y=x3-2×2+(m-1)x+2mvuông góc với đường thẳng y= – x
Hiển thị lời giải
Đạo hàm của hàm số đã cho là:
Câu 10: Tìm m để đồ thị : y=1/3 mx3+(m-1)x2+(3m-4)x+1 có điểm mà tiếp tuyến tại đó vuông góc với đường thẳng d: x- y+ 2013= 0.
Hiển thị lời giải
Đạo hàm của hàm số đã cho là : y’= mx2+ 2(m -1) x+ 3m- 4.
Đường thẳng d : x- y+ 2013= 0 ⇔ y= x+ 2013 đường thẳng này còn có thông số góc k= 1.
Để tiếp tuyến của đồ thị vuông góc với đường thẳng x- y+ 2013= 0 khi và chỉ khi hay mx2+2(m-1)x+3m-4=-1
hay mx2+2(m-1)x+3m-3=0 (*) có nghiệm.
+ Nếu m = 0 thì (*) trở thành: – 2x – 3= 0 hay x= (- 3)/2 ( thỏa mãn) .
+ Nếu m≠0 thì để phương trình ( *) có nghiệm ⇔ ∆’ ≥0
⇔ (m- 1)2 – m(3m- 3) ≥0 ⇔ mét vuông – 2m+ 1 – 3m2 + 3m ≥0
⇔ – 2m2 + m + 1 ≥0 ⇔ -1/2≤m≤1.
Vậy Đk -1/2≤m≤1 thỏa mãn nhu cầu đầu bài
Chọn B
Câu 11: Cho hàm số: y=2x+2/x-1 có đồ thị ( C). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến tuy nhiên tuy nhiên với đường thẳng d: y= – 4x+ 1.
Hiển thị lời giải
Câu 12: Cho hàm số: y=2x=2/x-1 có đồ thị ( C). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến tạo với 2 trục tọa độ lập thành một tam giác cân.
A. y= -x- 1; y= -x+ 6. B. y= -x- 1 ;y = -x+ 7
C. y= -x+ 2; y= -x+ 1 D. y= -x+ 1; y= -x+ 7
Hiển thị lời giải
Câu 13: Viết phương trình tiếp tuyến với đồ thị hàm số: y=2x/(x-1),biết thông số góc của tiếp tuyến bằng -2
Hiển thị lời giải
Câu 14: Viết phương trình tiếp tuyến với đồ thị hàm số: y=2x/(x-1) biết tiếp tuyến tuy nhiên tuy nhiên với đường thẳng (d): x+ 2y = 0
Hiển thị lời giải
Câu 15: Gọi (C) là đồ thị của hàm số x3/-x2+2x+1 . Viết phương trình tiếp tuyến của (C) vuông góc với đường thẳng y=-x/5+2
.
Hiển thị lời giải
Câu 16: Gọi (C) là đồ thị của hàm số y=x3/3-x2+2x+1. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đó cắt trục hoành , trục tung lần lượt tại A, B sao cho tam giác OAB vuông cân (O là gốc tọa độ ).
A. y = x +1/3 . B. y = x + 4/3. C. y = x + 4/13. D. y = x – 4/3.
Hiển thị lời giải
Vì tam giác OAB là tam giác vuông tại O nên nó chỉ hoàn toàn có thể vuông cân tại O , khi đó góc giữa tiếp tuyến (D) và trục Ox là ,suy ra thông số góc của (D) là “k” D =±1
+ Trường hợp “k” D =1 ,khi đó phương trình (D) : y = x + a. (a
Câu 17: Cho hàm số y=x3-2×2+(m-1)x+2m có đồ thị là (C). Tìm m để tiếp tuyến của đồ thị (C) tại điểm có hoành độ x= 1 tuy nhiên tuy nhiên với đường thẳng d: y= 3x+ 10.
A. m= 2 B. m= 4 C. m =0 D.Không tồn tại m
Hiển thị lời giải
Ta có:y’=3×2-4x +m-1 .
+ Tại x= 1 thì y(1)= 3m- 2 và y’(1)=m- 2
⇒Tiếp tuyến ∆ của (C) tại điểm có hoành độ x= 1 có phương trình
y=(m-2)(x-1)+3m-2=(m-2)x+2m
+ Để tiếp tuyến ∆// d khi và chỉ khi:
Vậy không tồn tại m thỏa mãn nhu cầu yêu cầu bài toán.
Chọn D.
Giới thiệu kênh Youtube Tôi
Trang trước
Trang sau
Đáp án cần chọn là: DGọi A và B lần lượt là giao điểm của đường thẳng (d) với trục Ox, OyKhi đó, Am−1m;0,B0,−m+1Gọi H là hình chiếu của O lên đường thẳng (d) thì OH đó đó là khoảng chừng cách từ điểm O tới đường thẳng (d)Xét tam giác vuông OAB có 1OH2=1OA2+1OB2⇔OH=OA.OBOA2+OB2Suy ra OHmin⇔OA.OBOA2+OB2minTa cóOA.OBOA2+OB2=m−1m−m+1m−1m2+m−12=(m−1)2(m−1)2(1+mét vuông)=m−11+m2Theo bất đẳng thức Cauchy-Schwarz thì m−11+mét vuông≤21+m21+mét vuông=2Vậy OHmin =2 và đạt được khi m = -1
Reply
3
0
Chia sẻ
Share Link Tải Cho đường thẳng d 2m – 5x y 1 + m = 0 tìm m sao cho khoảng chừng cách từ O đến d là a nhỏ nhất B lớn số 1 miễn phí
Bạn vừa tìm hiểu thêm tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Video Cho đường thẳng d 2m – 5x y 1 + m = 0 tìm m sao cho khoảng chừng cách từ O đến d là a nhỏ nhất B lớn số 1 tiên tiến và phát triển nhất và ShareLink Tải Cho đường thẳng d 2m – 5x y 1 + m = 0 tìm m sao cho khoảng chừng cách từ O đến d là a nhỏ nhất B lớn số 1 miễn phí.

Hỏi đáp vướng mắc về Cho đường thẳng d 2m – 5x y 1 + m = 0 tìm m sao cho khoảng chừng cách từ O đến d là a nhỏ nhất B lớn số 1
Nếu sau khi đọc nội dung bài viết Cho đường thẳng d 2m – 5x y 1 + m = 0 tìm m sao cho khoảng chừng cách từ O đến d là a nhỏ nhất B lớn số 1 vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Admin lý giải và hướng dẫn lại nha
#Cho #đường #thẳng #tìm #sao #cho #khoảng chừng #cách #từ #đến #là #nhỏ #nhất #lớn #nhất