Kinh Nghiệm về Cho hình chóp SABCD có đáy là hình bình hành Gọi MN lần lượt là trung điểm của AB và CD Chi Tiết
You đang tìm kiếm từ khóa Cho hình chóp SABCD có đáy là hình bình hành Gọi MN lần lượt là trung điểm của AB và CD được Update vào lúc : 2022-04-04 15:30:06 . Với phương châm chia sẻ Bí quyết Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Trang chủ
Sách ID
Khóa học miễn phí
Luyện thi ĐGNL và ĐH 2023
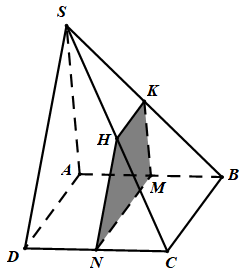
=> giao tuyến của (SCD) và (α) là NH// SD.
+ lại sở hữu HK là giao tuyến của (α) và (SBC) .
Thiết diện là tứ giác MNHK.
Ba mặt phẳng (ABCD) ; (SBC) và (α) đôi một cắt nhau theo những giao tuyến là MN; HK và BC mà MN// BC nên MN// HK. Vậy thiết diện là một hình thang .
Chọn B.
Page 2
Bằng cách Đk, bạn đồng ý với Điều khoản sử dụng và Chính sách Bảo mật của chúng tôi.
Cho hình chóp (S.ABCD) có đáy là hình bình hành. Gọi (M,,,N,,,P) lần lượt là trung điểm của (AB), (CD), (SA) (Tham khảo hình vẽ). Có bao nhiêu xác lập đúng trong những xác lập sau
i)(left( MNP right)parallel left( SBC right).) ii)(NPparallel left( SBC right).) 3i)(MPparallel left( SCD right).) 4i)(MPparallel left( SBC right).)
Hay nhất
a) i) Ta có: (left{beginarrayl MN//BC \ BCsubset (SBC) \ MNnotsubset (SBC) endarrayright. Rightarrow MN//(SBC).)
ii) Ta có: (left{beginarrayl MN//AD \ ADsubset (SAD) \ MNnotsubset (SAD) endarrayright. Rightarrow MN//(SAD).)
b) i) Ta thấy MP là đường trung bình trong tam giác SAB,
suy ra MP//SB.
Ta có: (left{beginarrayl SB//MP \ MPsubset (MNP) \ SBnotsubset (MNP) endarrayright. Rightarrow SB//(MNP).)
ii) Gọi (O=ACcap MN). Suy ra O là trung điểm AC.
Xét tam giác SAC ta có PO là đường trung bình.
Suy ra PO//SC.
Ta được~: (left{beginarrayl SC//PO \ POsubset (MNP) \ SCnotsubset (MNP) endarrayright. Rightarrow SC//(MNP).)
c) Gọi I là trung điểm BC.
Vì E là trọng tâm tam giác ABC nên (fracIEIA =frac13) . (1)
Vì F là trọng tâm tam giác SBC nên (fracIFIS =frac13 .) (2)
Từ (1),(2)suy ra EF//SA.
Ta có: (left{beginarrayl EF//SA \ SAsubset (SAC) \ EFnotsubset (SAC) endarrayright. Rightarrow EF//(SAC).)
Những vướng mắc liên quan
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và M; N lần lượt là trung điểm của AB; CD . Xác định thiết diện của hình chóp cắt bởi (α) trải qua MN và tuy nhiên tuy nhiên với mặt phẳng (SAD).Thiết diện là hình gì?
A. tứ giác
B. hình thang
C. hình thang cân
D. hình bình hành
- lý thuyết
- trắc nghiệm
- hỏi đáp
- bài tập sgk
Cho hình chóp SABCD, đáy là hình bình hành ABCD. Gọi M,N lần lượt là trung điểm SA,CD. Chứng minh MN // (SBC)?
help pls
Các vướng mắc tương tự
a) xét hình bình hành ABCD có M,N lần lượt là trung điểm của AB,CD
=> MN là đườg trung bình của hình bh
=> MN // AD // BC
+Xét mp (SBC) có
MN // BC
MN ∉ (SBC)
BC ∈ (SBC)
=> MN // (SBC)
(cmtt với MN // (SAD))
b) xét tam giác SAB có M,P lần lượt là trung điểm của cạch AB, SA
=> MP là đường trung bình của Δ SAB
=> MP // SB
Xét mp(SBC) và mp (MNP) :
MN// BC
MP// SB
MN ∩ MP = M
BC ∩ SB = B
=> (MNP) // (SBC)
mà SB,SC thuộc mp(SBC)
=> SB//(MNP)
SC// (MNP)
Chia Sẻ Link Tải Cho hình chóp SABCD có đáy là hình bình hành Gọi MN lần lượt là trung điểm của AB và CD miễn phí
Bạn vừa đọc nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Clip Cho hình chóp SABCD có đáy là hình bình hành Gọi MN lần lượt là trung điểm của AB và CD tiên tiến và phát triển nhất và Chia SẻLink Tải Cho hình chóp SABCD có đáy là hình bình hành Gọi MN lần lượt là trung điểm của AB và CD miễn phí.

Hỏi đáp vướng mắc về Cho hình chóp SABCD có đáy là hình bình hành Gọi MN lần lượt là trung điểm của AB và CD
Nếu sau khi đọc nội dung bài viết Cho hình chóp SABCD có đáy là hình bình hành Gọi MN lần lượt là trung điểm của AB và CD vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Tác giả lý giải và hướng dẫn lại nha
#Cho #hình #chóp #SABCD #có #đáy #là #hình #bình #hành #Gọi #lần #lượt #là #trung #điểm #của #và