Kinh Nghiệm về Gọi B là số giao điểm của hai đồ thị y = x mũ 3 trừ x bình 1 và y = x bình Công 1 tìm B Chi Tiết
Bạn đang tìm kiếm từ khóa Gọi B là số giao điểm của hai đồ thị y = x mũ 3 trừ x bình 1 và y = x bình Công 1 tìm B được Update vào lúc : 2022-04-14 13:10:08 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Phương pháp giải:
Nội dung chính
- CÂU HỎI HOT CÙNG CHỦ ĐỀ
- Số giao điểm của hai đồ thị hàm số y = 3(x^2) và y = (x^3) + (x^2) + x + 1 là:
- Số giao điểm của đồ thị hàm số y = (x^3) – 2(x^2) + x – 1 và đường thẳng y = 1 – 2x là:
- lý thuyết
- trắc nghiệm
- hỏi đáp
- bài tập sgk
a) Lập bảng giá trị những điểm mà đồ thị hàm số trải qua tiếp theo đó vẽ đồ thị những hàm số đã cho.
b) Giải phương trình hoành độ giao điểm của 2 đồ thị hàm số ta tìm kiếm được hoành độ giao điểm.
Thế hoành độ giao điểm đó vào một trong những trong hai công thức hàm số của 2 đường thẳng đã cho ta tìm kiếm được tung độ của giao điểm. Từ đó ta có tọa độ giao vấn đề cần tìm
c) Tính OB, AH (H là hình chiếu của A trên OB) để tính diện tích s quy hoạnh tam giác OAB.
Lời giải rõ ràng:
a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ.
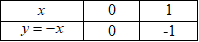
Ta có bảng giá trị của hai hàm số:
Đồ thị hàm số (y = – x)là đường thẳng trải qua hai điểm (Oleft( 0;0 right);Eleft( 1; – 1 right))
Đồ thị hàm số (y = 2x + 6)là đường thẳng trải qua hai điểm (Fleft( – 1;4 right);,Gleft( – 3;0 right))
b) Gọi (A) là giao điểm của hai đồ thị nói trên. Tìm tọa độ điểm (A.)
Xét phương trình hoành độ giao điểm của hai hàm số: (y = – x)và(y = 2x + 6)ta có:
( – x = 2x + 6,,, Rightarrow – 3x = 6,,, Rightarrow x = – 2)
Thay (x = – 2) vào phương trình: (y = – x) ta được (y = 2).
Vậy giao điểm (A) của hai đồ thị hàm số có tọa độ là (Aleft( – 2;2 right)).
c) Gọi (B) là giao điểm của đồ thị hàm số (y = 2x + 6) với trục tung. Tính diện tích s quy hoạnh của tam giác (OAB) (với (O) là gốc tọa độ và cty trên những trục tọa độ là xentimet).
Ta có (B) là giao điểm của đồ thị hàm số (y = 2x + 6)với trục tung nên (x_B = 0 Rightarrow y_B = 2x_B + 6 = 6, Rightarrow Bleft( 0;6 right))
( Rightarrow OB = 6,,,left( cm right))
Gọi (H) là hình chiếu của (A) trên (Oy,) khi đó ta sẽ có được: (AH bot OB = left H right\) và (AH = left| x_A right| = 2,,,left( cm right))
Suy ra (S_OAB = frac12.AH.OB = frac12.2.6 = 6,,,,left( cm^2 right))
Vậy diện tích s quy hoạnh tam giác (OAB) là (6,,cm^2).
Chọn C.
Trang chủ
Sách ID
Khóa học miễn phí
Luyện thi ĐGNL và ĐH 2023
cho hàm số y=x^2 có đồ thị (P). Gọi A và B là 2 điểm thuộc (P) lần lượt có hoành độ là -1 và 2. Viết phương trình đường thẳng AB
Các vướng mắc tương tự
Số giao điểm của đồ thị hàm số (y = x^3 – 4x + 1) và đường thẳng (y = x + 1) bằng
Giải rõ ràng:
Phương trình hoành độ giao điểm :
(frac2x+1x+1=-x-1,,(xne -1)Leftrightarrow 2x+1=-x^2-2x-1Leftrightarrow x^2+4x+2=0)
Gọi (x_1,,,x_2) là 2 nghiệm của phương trình trên. Theo Vi – ét, ta có: (x_1+x_2=-4,,,,,,x_1.x_2=2.)
Tọa độ những điểm (A(x_1;y_1),,,B(x_2;y_2)).
Độ dài đoạn AB:
(beginarraylAB = sqrt (x_2 – x_1)^2 + (y_2 – y_1)^2 = sqrt (x_2 – x_1)^2 + left[ ( – x_2 – 1) – left( – x_1 – 1 right) right]^2 = sqrt 2(x_2 – x_1)^2 \,,,,,,,,, = sqrt 2(x_2 + x_1)^2 – 8x_2x_1 = sqrt 2.( – 4)^2 – 8.2 = 4.endarray)
Chọn: A.
Đáp án D.
Phương trình hoành độ giao điểm: x3 + x – 2 = x – 1 <=> x3 = 1 <=> x = 1.
Vậy (C) và đường thẳng y = x – 1 chỉ có một giao điểm
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Số giao điểm của hai đồ thị hàm số y = 3(x^2) và y = (x^3) + (x^2) + x + 1 là:
Câu 1009 Thông hiểu
Số giao điểm của hai đồ thị hàm số $y = 3x^2$ và $y = x^3 + x^2 + x + 1$ là:
Đáp án đúng: b
Phương pháp giải
– Bước 1: Lập phương trình hoành độ giao điểm .
– Bước 2: Khảo sát sự biến thiên của hàm số $hleft( x right) = fleft( x right) – gleft( x right)$ trên TXĐ.
+ Tính $h’left( x right)$, giải phương trình $h’left( x right) = 0$ tìm những nghiệm và những điểm $h’left( x right)$ không xác lập.
+ Xét dấu $h’left( x right)$ và lập bảng biến thiên.
– Bước 3: Kết luận số giao điểm của hai đồ thị hàm số $y = fleft( x right)$ và $y = gleft( x right)$.
+ Số giao điểm của hai đồ thị hàm số $y = fleft( x right)$ và $y = gleft( x right)$ là số giao điểm của đồ thị hàm số $hleft( x right)$ với trục hoành (đường thẳng $y = 0$)
Phương pháp giải những bài toán tương giao đồ thị — Xem rõ ràng
…
Số giao điểm của đồ thị hàm số y = (x^3) – 2(x^2) + x – 1 và đường thẳng y = 1 – 2x là:
Câu 1004 Thông hiểu
Số giao điểm của đồ thị hàm số $y = x^3 – 2x^2 + x – 1$ và đường thẳng $y = 1 – 2x$ là:
Đáp án đúng: d
Phương pháp giải
– Xét phương trình hoành độ giao điểm của $d$ và $left( C right)$.
– Nêu quan hệ giữa số nghiệm của phương trình và số giao điểm của $d$ và $left( C right)$.
– Giải phương trình tìm nghiệm và kết luận.
Phương pháp giải những bài toán tương giao đồ thị — Xem rõ ràng
…
Share Link Tải Gọi B là số giao điểm của hai đồ thị y = x mũ 3 trừ x bình 1 và y = x bình Công 1 tìm B miễn phí
Bạn vừa đọc tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Clip Gọi B là số giao điểm của hai đồ thị y = x mũ 3 trừ x bình 1 và y = x bình Công 1 tìm B tiên tiến và phát triển nhất và Share Link Down Gọi B là số giao điểm của hai đồ thị y = x mũ 3 trừ x bình 1 và y = x bình Công 1 tìm B miễn phí.

Giải đáp vướng mắc về Gọi B là số giao điểm của hai đồ thị y = x mũ 3 trừ x bình 1 và y = x bình Công 1 tìm B
Nếu sau khi đọc nội dung bài viết Gọi B là số giao điểm của hai đồ thị y = x mũ 3 trừ x bình 1 và y = x bình Công 1 tìm B vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Ad lý giải và hướng dẫn lại nha
#Gọi #là #số #giao #điểm #của #hai #đồ #thị #mũ #trừ #bình #và #bình #Công #tìm