Kinh Nghiệm về Tìm giá trị lớn số 1 của hàm số 2 yxx Mới Nhất
Quý khách đang tìm kiếm từ khóa Tìm giá trị lớn số 1 của hàm số 2 yxx được Update vào lúc : 2022-04-24 14:10:06 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi tìm hiểu thêm Post vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Câu hỏi hot cùng chủ đề
Nội dung chính
- II. Cách tính giá trị lớn số 1 của hàm số và giá trị nhỏ nhất của hàm số trên một đoạn
- III. Chú ý
- Bài tập giá trị lớn số 1 của hàm số và giá trị nhỏ nhất của hàm số :
Cách chuyển từ sin sang cos ạ ?
Trả lời (30) Xem đáp án »
Cho hàm số y=ax3+bx2+cx+d có đồ thị như hình vẽ. Tìm mệnh đề đúng
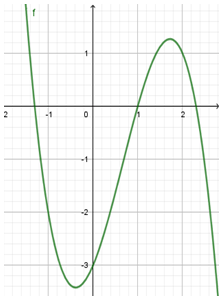
A. a<0, b>0, c>0, d<0
B. a<0, b<0, c>0, d<0
C. a>0, b>0, c>0, d<0
D. a<0, b>0, c<0, d<0
- Tìm những điểm xi ∈ (a ; b)(i = 1, 2, . . . , n) mà tại đó f'(xi) = 0 hoặc f'(xi) không xác lập.
- Tính f(a), f(b), f(xi) (i = 1, 2, . . . , n) .
- Khi đó: max [a;b] f(x)=max f(a);f(b);f(xi)
- Tìm những điểm x1; x²; x³…; xn thuộc đoạn [a; b] mà tại đó hàm số có đạo hàm f′(x)=0 hoặc không còn đạo hàm.
- Tính f(x1); f(x²); f(x³);…; f(xn) và f(a); f(b)
- So sánh những giá trị tìm kiếm được ở trên. Giá trị lớn số 1 trong những giá trị đó đó đó là GTLN của hàm số y=f(x) trên [a; b] và giá trị nhỏ nhất trong những giá trị đó đó đó là GTNN của hàm số y=f(x) trên [a; b]
LIVESTREAM 2K4 ÔN THI THPT QUỐC GIA 2022
PHƯƠNG TRÌNH ĐƯỜNG TRÒN – 2k6 – Livestream TOÁN thầy ANH TUẤN
Gv. Lê Ngọc – Phát trực tiếp 1 ngày trước
Toán
ÔN THI VÀO 10 – GIẢI ĐỀ THI THỬ THCS DỊCH VỌNG HÀ NỘI – 2k7 – Livestream TOÁN thầy QUANG HUY
Gv. Lê Ngọc – Phát trực tiếp 2 ngày trước
Toán
CHỮA ĐỀ THAM KHẢO CUỐI HỌC KÌ 2 – 2K5 Livestream LÝ THẦY TUYÊN
Gv. Lê Ngọc – Phát trực tiếp 2 ngày trước
Vật lý
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2 SÁT NHẤT – 2k5 – Livestream HÓA cô THU
Gv. Nguyễn Thị Thu – Phát trực tiếp 2 ngày trước
Hóa học
CHỮA ĐỀ THI CUỐI HỌC KÌ 1 – THPT NGUYỄN HUỆ – 2K5 – Livestream HÓA cô HUYỀN
Gv. Cô Phạm Huyền – Phát trực tiếp 2 ngày trước
Hóa học Xem thêm …

Cho hàm số y = f(x) xác lập trên tập D.
Giá trị lớn số 1 của hàm số
Số M là giá trị lớn số 1 (GTLN) của hàm số f trên D
⇔f(x)≤M,∀x∈D
∃x0∈D sao cho f(x0)=M
Kí hiệu : M=maxD f(x).
Giá trị nhỏ nhất của hàm số
Số m là giá trị nhỏ nhất (GTNN) của hàm số f trên D
⇔f(x)≥m,∀x∈D
∃x0∈D sao cho f(x0)=m
Kí hiệu: m=minD f(x).
II. Cách tính giá trị lớn số 1 của hàm số và giá trị nhỏ nhất của hàm số trên một đoạn
Định lí
Hàm số liên tục trên một đoạn thì có GTLN và GTNN trên đoạn đó.
Quy tắc tìm GTLN, GTNN của hàm số y=f(x) liên tục trên đoạn [a ; b]
min [a;b] f(x)=min f(a);f(b);f(xi)
III. Chú ý
Để tìm GTLN, GTNN của hàm số y=f(x) xác lập trên tập hợp D, ta hoàn toàn có thể khảo sát sự biến thiên của hàm số trên D, rồi vị trí căn cứ vào bảng biến thiên của hàm số mà kết luận về GTLN và GTNN của hàm số.
Bài tập giá trị lớn số 1 của hàm số và giá trị nhỏ nhất của hàm số :
Bài 1 : Tính giá trị lớn số 1 của hàm số và giá trị nhỏ nhất
Lời giải A
Xét tính đồng biến, nghịch biến và tính giá trị lớn số 1, giá trị nhỏ nhất của hàm số:
y = x² trên đoạn [-3; 0];
Lời giải rõ ràng:
y’ = 2x ≤ 0 trên đoạn [-3; 0].
Vậy hàm số nghịch biến trên đoạn [-3,0].
Khi đó trên đoạn [-3,0]: hàm số đạt giá trị lớn số 1 tại x = -3 và giá trị lớn số 1 bằng 9, hàm số đạt giá trị nhỏ nhất tại x = 0 và giá trị nhỏ nhất = 0.
Lời giải B
y=x+1x−1y=x+1x−1 trên đoạn [3; 5].
Lời giải rõ ràng:
y′=−2(x−1)2<0 trên đoạn [3; 5].
Vậy hàm số nghịch biến trên đoạn [3; 5].
Khi đó trên đoạn [-3,5]: hàm số đạt giá trị lớn số 1 tại x = 3 và giá trị lớn số 1 bằng 2, hàm số đạt giá trị nhỏ nhất tại x = 5 và giá trị nhỏ nhất = 1.5.
Bài 2 :Tính giá trị lớn số 1, giá trị nhỏ nhất của hàm số
y=x³−3x²−9x+35 trên những đoạn [−4;4] và [0;5]
Phương pháp giải:
Để tìm GTLN, GTNN của hàm số y=f(x) trên đoạn [a; b] ta làm như sau :
+) Tìm những điểm x1; x²; x³…; xn thuộc đoạn [a; b] mà tại đó hàm số có đạo hàm f′(x)=0 hoặc không còn đạo hàm.
+) Tính f(x1); f(x²); f(x³);…; f(xn) và f(a); f(b)
+) So sánh những giá trị tìm kiếm được ở trên. Giá trị lớn số 1 trong những giá trị đó đó đó là GTLN của hàm số y=f(x) trên [a; b] và giá trị nhỏ nhất trong những giá trị đó đó đó là GTNN của hàm số y=f(x) trên [a; b]
max x∈[a; b]f(x)=max f(x1); f(x²);…; f(xm); f(a); f(b).
min x∈[a; b]f(x)=min f(x1); f(x²);…; f(xm); f(a); f(b).
Lời giải rõ ràng:
y=x³−3x²−9x+35
Xét D=[−4; 4] có :
y′=3x²−6x−9⇒y′=0⇔3x²−6x−9=0 ⇔ x=3 ∈D
x=−1 ∈D
Ta có : y(−4)=−41;y(1)=40; y(3)=8;y(4)=15.
Vậy max x∈[−4; 4] y=40 khi x=−1 và min x∈[−4; 4] y=−41 khi x=−4.
Xét D=[0; 5] có:
y′=3x²−6x−9y′ ⇒y′=0⇔3x²−6x−9=0 ⇔ [x=3 ∈D
x=−1 ∉D
Ta có : y(0)=35; y(3)=8; y(5)=40
Vậy max x∈[0; 5] y=40 khi x=5 và minx∈[0; 5]y=8 khi x=3.
Lời giải B
y=x4−3x²+2 trên những đoạn [0;3] và [2;5];
Lời giải rõ ràng:
y=x4−3x²+2
Ta có:y′=4x³−6x ⇒y′=0⇔4x³−6x=0
⇔ x=0
x=√(3/2)=√6/2
x=−√(3/2)=−√6/2
Xét D=[0; 3] có: x=−√6/2∉D
Có: y(0)=2; y(3)=56;; y(√6/2)=−1/4.
Vậy minx ∈[0; 3] y=−1/4 khi x=√6/2 và max x∈[0; 3] y=56 khi x=3.
Xét D=[2; 5] ta thấy x=0; x=±√6/2 ∉ D
Có y(2)=6; y(5)=552.
Vậy minx ∈[2; 5] y=6 khi x=2 và max x∈[2; 5 ]y=552 khi x=5.
Bài 3 :Tính giá trị lớn số 1, giá trị nhỏ nhất của hàm số:
y=x³−3x²−9x+35 trên những đoạn [−4;4] và [0;5]
Phương pháp giải:
Để tìm GTLN, GTNN của hàm số y=f(x) trên đoạn [a; b] ta làm như sau :
maxx∈[a; b]f(x)=maxf(x1); f(x²);…; f(xm); f(a); f(b).
minx∈[a; b]f(x)=minf(x1); f(x²);…; f(xm); f(a); f(b).
Lời giải rõ ràng:
y=x³−3x²−9x+35
Xét D=[−4; 4] có :
y′=3x²−6x−9⇒y′=0⇔3x²−6x−9=0 ⇔ x=3 ∈D
x=−1 ∈D
Ta có : y(−4)=−41;y(1)=40; y(3)=8;y(4)=15.
Vậy max x∈[−4; 4] y=40 khi x=−1 và min x∈[−4; 4] y=−41 khi x=−4.
Xét D=[0; 5] có:
y′=3x²−6x−9y′ ⇒y′=0⇔3x²−6x−9=0 ⇔ [x=3 ∈D
x=−1 ∉D
Ta có : y(0)=35; y(3)=8; y(5)=40
Vậy max x∈[0; 5] y=40 khi x=5 và minx∈[0; 5]y=8 khi x=3.
LG b
y=x4−3x²+2 trên những đoạn [0;3] và [2;5];
Lời giải rõ ràng:
y=x4−3x²+2
Ta có: y′=4x³−6x ⇒y′=0⇔4x³−6x=0
⇔ x=0
x=√(3/2)=√6/2
x=−√(3/2)=−√6/2
Xét D=[0; 3] có: x=−√6/2∉D
Có: y(0)=2; y(3)=56;; y(√6/2)=−1/4.
Vậy minx∈[0; 3] y=−14 khi x=√ và max x∈[0; 3] y=56 khi x=3.
Xét D=[2; 5] ta thấy x=0; x=±√62 ∉ D
Có y(2)=6; y(5)=552.
Vậy min x∈[2; 5] y=6 khi x=2 và max x∈[2; 5 ]y=552 khi x=5.
Để tìm hiểu thêm về lý thuyết môn Toán lớp 12 những bạn hoàn toàn có thể tìm hiểu thêm TẠI ĐÂY
Để tìm hiểu thêm thêm về đề thi mẫu môn Toán liên quan tới giá trị lớn số 1 của hàm số và giá trị nhỏ nhất của hàm số những bạn hoàn toàn có thể bấm TẠI ĐÂY
Share Link Tải Tìm giá trị lớn số 1 của hàm số 2 yxx miễn phí
Bạn vừa Read nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Review Tìm giá trị lớn số 1 của hàm số 2 yxx tiên tiến và phát triển nhất và Chia Sẻ Link Down Tìm giá trị lớn số 1 của hàm số 2 yxx Free.

Thảo Luận vướng mắc về Tìm giá trị lớn số 1 của hàm số 2 yxx
Nếu sau khi đọc nội dung bài viết Tìm giá trị lớn số 1 của hàm số 2 yxx vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Admin lý giải và hướng dẫn lại nha
#Tìm #giá #trị #lớn #nhất #của #hàm #số #yxx