Thủ Thuật Hướng dẫn Tìm giá trị nhỏ nhất m của hàm số f x ln x căn x 2 e 2 Chi Tiết
Bạn đang tìm kiếm từ khóa Tìm giá trị nhỏ nhất m của hàm số f x ln x căn x 2 e 2 được Cập Nhật vào lúc : 2022-04-17 15:10:06 . Với phương châm chia sẻ Kinh Nghiệm về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi tìm hiểu thêm nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Admin lý giải và hướng dẫn lại nha.
Bài toán tìm giá trị lớn số 1 (GTLN), giá trị nhỏ nhất (GTNN) của hàm số xuất hiện khá thường xuyên trong những đề thi toán học. Với nhiều mức độ, nhiều dạng rất khác nhau. Hiểu được sự trở ngại vất vả của học viên khi khởi đầu tiếp xúc với những dạng bài này, bài học kinh nghiệm tay nghề ngày hôm nay VerbaLearn sẽ tổng hợp lại rõ ràng những dạng toán và kiến thức và kỹ năng liên quan đến GTLN, GTNN trong toán học và nhất là chương trình toán lớp 12.
Nội dung chính
- Lý thuyết giá trị lớn số 1 nhỏ nhất của hàm số
- Phân dạng bài tập tìm GTLN GTNN của hàm số
- Dạng 1: Tìm giá trị lớn số 1 nhỏ nhất của hàm số y = f(x) trên một khoảng chừng
- Dạng 2: Tìm giá trị lớn số 1 nhỏ nhất của hàm số trên một đoạn
- Dạng 3: Tìm giá trị lớn số 1 nhỏ nhất của hàm số y = |f(x)| trên đoạn [a; b]
- Dạng 4: Tìm Đk tham số để GTLN của hàm số y = |f(x) + g(m)| trên đoạn [a; b] đạt GTNN
- Dạng 5: Tìm giá trị lớn số 1 giá trị nhỏ nhất lúc cho đồ thị hoặc bảng biến thiên
- Dạng 6. Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số lượng giác
- Dạng 7. Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số khác
- Dạng 8. Tìm giá trị lớn số 1, giá trị nhỏ nhất của biểu thức nhiều biến
- Dạng 9. Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số y = f(u(x)), y = f(u(x)) ± h(x)… lúc biết bảng biến thiên hoặc đồ thị của hàm số y = f(x).
- Dạng 10. Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số y = f(u(x)), y = f(u(x)) ± h(x)… Khi biết đồ thị của hàm số y = f’(x)
- Dạng 11. Ứng dụng của giá trị lớn số 1 và nhỏ nhất trong những bài toán thực tiễn
- Dạng 12. Tìm m để F(x; m) = 0 có nghiệm trên tập D
- Dạng 13. Tìm m để bất phương trình F(x; m) > 0; F(x; m) ≥ 0; F(x; m) < 0; F(x; m) ≤ 0 có nghiệm trên tập D.
- Tài liệu tìm GTLN GTNN của hàm số
- #1. Các dạng toán GTLN GTNN thường gặp trong kỳ thi THPT QG
- #2. Bài tập GTLN GTNN của hàm số
- #3. Bài tập vận dụng cao GTLN GTNN của hàm số
- #4. Tổng ôn trắc nghiệm GTLN GTNN của hàm số
- #5. GTLN GTNN của hàm giá trị tuyệt đối
- #6. Bài tập GTLN GTNN của hàm số
- #7. Tóm tắt lý thuyết và bài tập trắc nghiệp GTLN GTNN của hàm số
- #8. Các bài tập VDC GTLN và GTNN của hàm số
- #9. GTLN GTNN của hàm hợp hàm link
- #10. GTNN GTLN của hàm số trị tuyệt đối
- Bước 1. Tìm tập xác lập (nếu đề chưa cho khoảng chừng)
- Bước 2. Tính y’ = f’(x); tìm những điểm mà đạo hàm bằng không hoặc không xác lập.
- Bước 3. Lập bảng biến thiên
- Bước 4. Kết luận
- Bước 1. Tính f’(x)
- Bước 2. Tìm những điểm xi ∈ (a;b) mà tại đó f’(xi) = 0 hoặc f’(xi) không xác lập
- Bước 3. Tính f(a), f(xi), f(b)
- Bước 4. Tìm số lớn số 1 M và số nhỏ nhất m trong những số trên.
- Bước 1. Đặt ẩn phụ và tìm Đk cho ẩn phụ
- Bước 2. Giải bài toán tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số theo ẩn phụ
- Bước 3. Kết luận (Chọn đáp án)
- Bước 1. Cô lập tham số m và đưa về dạng g(m) > f(x) hoặc g(m) ≥ f(x) hoặc g(m) < f(x) hoặc g(m) ≤ f(x)
- Bước 2. Khảo sát sự biến thiên của hàm số f(x) trên D
- Bước 3. Dựa vào bảng biến thiên xác lập những giá trị của tham số m
- Bước 4. Kết luận
Lý thuyết giá trị lớn số 1 nhỏ nhất của hàm số
Cho hàm số y = f(x) xác lập trên tập D.
+) Số M được gọi là giá trị lớn số 1 (GTLN) của hàm số y = f(x) trên tập D nếu f(x) ≤ M với mọi x ∈ D và tồn tại x0 ∈ D sao cho f(x0) = M.
Kí hiệu: 
+) Số m được gọi là giá trị nhỏ nhất (GTNN) của hàm số y = f(x) trên tập D nếu f(x) ≥ M với mọi x ∈ D và tồn tại x0 ∈ D sao cho f(x0) = M.
Kí hiệu: 
Sơ đồ khối mạng lưới hệ thống hóa:
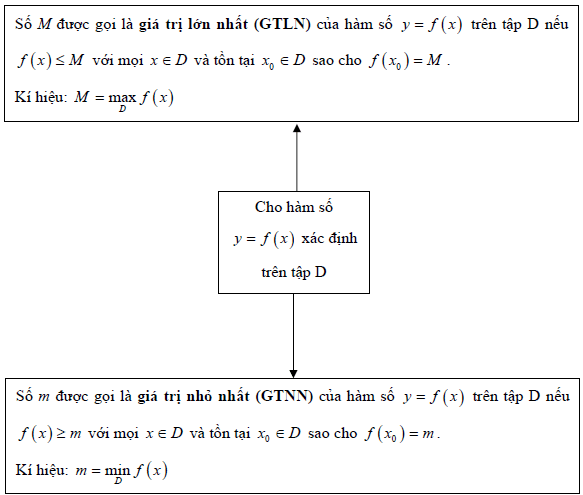
Phân dạng bài tập tìm GTLN GTNN của hàm số
Thông thường riêng với những bài giảng về giá trị lớn số 1 giá trị nhỏ nhất chỉ có cơ bản vài dạng bài tập. Tuy nhiên riêng với một nội dung bài viết tổng quan về chuyên đề như này thì VerbaLearn phân thành 13 dạng từ cơ bản, vận dụng cho tới vận dụng cao. Nếu những dạng bài tập quá dài bạn đọc hoàn toàn có thể tải những tài liệu về để xem một cách thuận tiện và đơn thuần và giản dị hơn.
Dạng 1: Tìm giá trị lớn số 1 nhỏ nhất của hàm số y = f(x) trên một khoảng chừng
Phương pháp giải
Ta thực thi tiến trình sau:
Lưu ý: Có thể dùng máy tính cầm tay để giải theo tiến trình như sau:
Bước 1. Để tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số y = f(x) trên miền (a;b) ta sử dụng máy tính Casio với lệnh MODE 7 (MODE 9 lập bảng giá trị)
Bước 2. Quan sát bảng giá trị máy tính hiển thị, giá trị lớn số 1 xuất hiện là max, giá trị nhỏ nhất xuất hiện là min.
– Ta thiết lập miền giá trị của biến x Start a End b Step (hoàn toàn có thể làm tròn để Step đẹp).
Chú ý: Khi đề bài liên có những yếu tố lượng giác sinx, cosx, tanx… ta chuyển máy tính về chính sách Radian.
Bài tập mẫuVí dụ 1. Cho hàm số . Khẳng định nào sau này đúng?
A.
B.
C.
D. Hàm số không tồn tại giá trị lớn số 1
Hướng dẫn giải
Chọn B
Tập xác lập D = ℝ
Ta có f’(x) = -2×5 + 2×4 – x + 1 = – (x – 1)(2×4 + 1)
Khi đó f’(x) = 0 ⇔ – (x – 1)(2×4 + 1) = 0 ⇔ x = 1
Bảng biến thiên
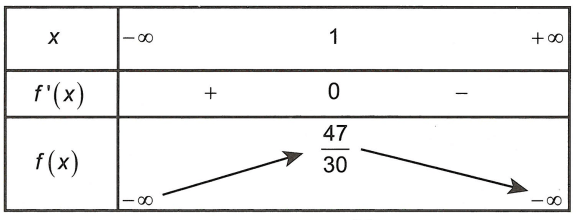
Dựa vào bảng biến thiên, ta thấy tại x = 1
Ví dụ 2. Gọi a là giá trị lớn số 1 của hàm số trên khoảng chừng (-∞; 1). Khi đó giá trị của biểu thức
bằng
A.
B.
C.
D.
Hướng dẫn giải
Chọn C
Hàm số liên tục trên khoảng chừng (-∞; 1)
Ta có
Khi đó f’(x) = 0 ⇔ 8×2 – 12x – 8 = 0 ⇔
Bảng biến thiên
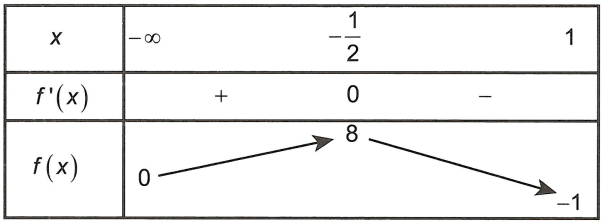
Dựa vào bảng biến thiên, ta thấy
Ví dụ 3. Cho hàm số . Trong những xác lập sau, xác lập nào đúng?
A.
B.
C.
D. Hàm số không còn mức giá trị nhỏ nhất
Hướng dẫn giải
Chọn B
Tập xác lập D = ℝ
Ta có
Do đó y’ = 0 ⇔ 2×2 – 2 = 0 ⇔ x = ±1
Bảng biến thiên
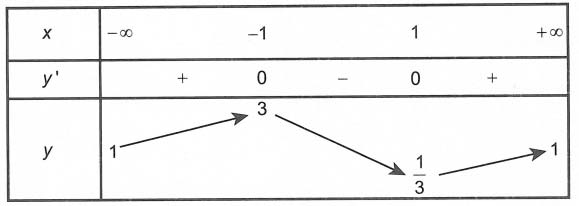
Dựa vào bảng biến thiên, ta thấy tại x = 1
Dạng 2: Tìm giá trị lớn số 1 nhỏ nhất của hàm số trên một đoạn
Phương pháp giải
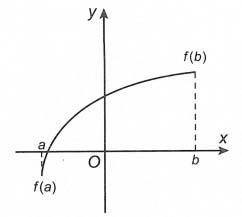
Khi đó và
Chú ý:
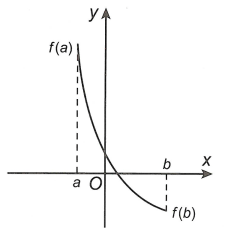
– Hàm số y = f(x) đồng biến trên đoạn [a;b] thì
– Hàm số y = f(x) nghịch biến trên đoạn [a;b] thì
Bài tập 1. Cho hàm số . Giá trị của
bằng
A. 16
B.
C.
D.
Hướng dẫn giải
Chọn D
Ta có ; do đó hàm số nghịch biến trên mỗi khoảng chừng (-∞; 1); (1; +∞)
⇒ Hàm số nghịch biến trên [2; 3].
Do đó
Vậy
Bài tập 2. Gọi M, m lần lượt là giá trị lớn số 1 và nhỏ nhất của hàm số . Giá trị của biểu thức P = M + m bằng
A.
B.
C.
D.
Hướng dẫn giải
Chọn A
Tập xác lập D = [-2; 2]
Ta có , x ∈ (-2; 2)
y’ = 0 ⇔
Vậy
Bài tập 3. Giá trị nhỏ nhất của hàm số y = 2×3 – 3×2 + m trên đoạn [0; 5] bằng 5 khi m bằng
A. 6
B. 10
C. 7
D. 5
Hướng dẫn giải
Chọn A.
Hàm số xác lập và liên tục trên D = [0; 5]
Ta có y’ = 0 ⇔ 6×2 – 6x = 0 ⇔
f (0) = m; f (1) = m – 1; f (5) = 175 + m
Dễ thấy f (5) > f (0) > f (1), ∀ m ∈ ℝ nên
Theo đề bài ⇔ m – 1 = 5 ⇔ m = 6
Bài tập 4. Gọi A, B là giá trị nhỏ nhất, giá trị lớn số 1 của hàm số trên đoạn [2; 3]. Tất cả những giá trị thực của tham số m để
là
A. m = 1; m = -2
B. m = -2
C. m = ±2
D. m = -1; m = 2
Hướng dẫn giải
Chọn A
Hàm số đã cho liên tục trên đoạn [2; 3]
Ta có
Do đó
⇔ 3m2 + m – 6 = 0 ⇔
Bài tập 5. Biết hàm số y = x3 + 3mx2 + 3(2m – 1) x + 1 (với m là tham số) trên đoạn [-2; 0] đạt giá trị lớn số 1 bằng 6. Các giá trị của tham số m là
A. m = 1
B. m = 0
C. m = 3
D. m = -1
Hướng dẫn giải
Chọn D
y’ = 0 ⇔
Vì y(-2) = -1; y(0) = 1 và theo bài ra nên giá trị lớn số 1 không đạt tại x = -2; x = 0.
Do đó giá trị lớn số 1 đạt tại y(-1) hoặc y(1 – 2m).
Ta có y(-1) = -3m + 3; y(1 – 2m) = (1 – 2m)2(m – 2) + 1
Trường hợp 1: Xét -3m + 3 = 6 ⇔ m = -1
Thử lại với m = -1, ta có y’ = 0 ⇔ nên m = -1 là một giá trị cần tìm.
Trường hợp 2: Xét
Vì ⇒ m – 2 < 0 ⇒ (1 – 2m)2(m – 2) < 0 nên (1) vô nghiệm
Dạng 3: Tìm giá trị lớn số 1 nhỏ nhất của hàm số y = |f(x)| trên đoạn [a; b]
Phương pháp giải
Thực hiện theo tiến trình sau
– Bước 1. Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số f(x) trên đoạn [a; b], giả sử thứ tự là M, m.
– Bước 2.
+) Tìm
+) Tìm
Trường hợp 1: M․m < 0 ⇒ = 0
Trường hợp 1: m ≥ 0 ⇒ = m
Trường hợp 1: M ≤ 0 ⇒ = |M| = -M
– Bước 3. Kết luận.
* Tìm tham số để GTLN của hàm số y = |f(x)| trên đoạn [α, β] bằng k. Thực hiện theo tiến trình sau:
– Bước 1. Tìm
– Bước 2. Xét những trường hợp
+) |A| = k tìm m, thử lại những giá trị m đó
+) |B| = k tìm m, thử lại những giá trị m đó
Bài tập mẫuBài tập 1. Giá trị nhỏ nhất của hàm số y = |x3 – 9×2 + 24x – 68| trên đoạn [-1; 4] bằng
A. 48
B. 52
C. -102
D. 0
Hướng dẫn giải
Chọn A
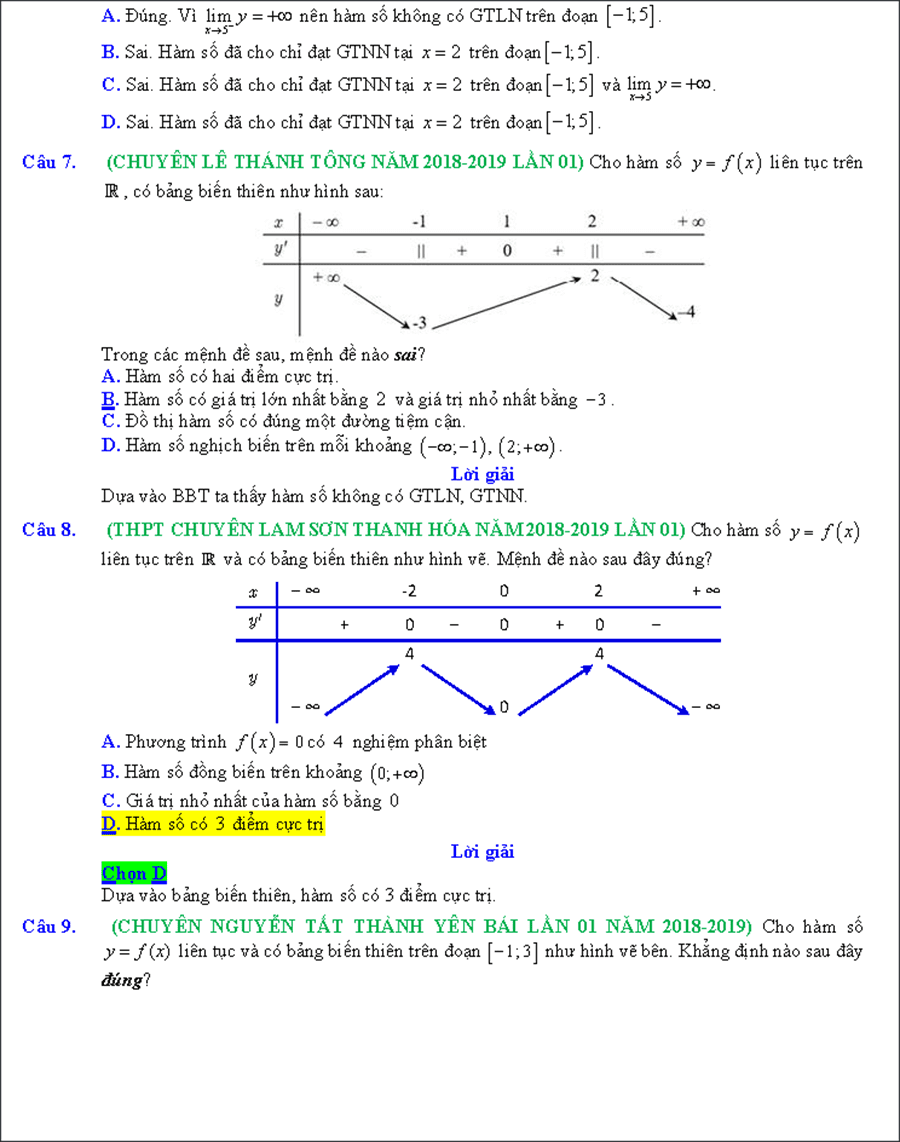
Bảng biến thiên của hàm số y = x3 – 9×2 + 24x – 68 trên đoạn [-1; 4]
![Dạng 3: Tìm giá trị lớn nhất nhỏ nhất của hàm số y = |f(x)| trên đoạn [a; b]](https://sg.cdnki.com/tim-gia-tri-nho-nhat-m-cua-ham-so-f-x-ln-x-can-x-2-e-2---aHR0cHM6Ly92ZXJiYWxlYXJuLmNvbS93cC1jb250ZW50L3VwbG9hZHMvMjAyMC8wNS90aW0tZ2lhLXRyaS1sb24tbmhhdC1uaG8tbmhhdC1jdWEtaGFtLXNvLTcucG5n.webp)
Suy ra bảng biến thiên của hàm số y = |x3 – 9×2 + 24x – 68| trên đoạn [-1; 4] là
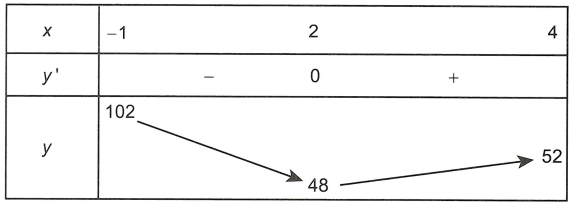
Vậy giá trị nhỏ nhất của hàm số y = |x3 – 9×2 + 24x – 68| trên đoạn [-1; 4] bằng 48.
Cách khác: Theo trường hợp 3 thì M = -48 < 0 ⇒ min y = 48
Bài tập 2: Gọi S là tập hợp toàn bộ những giá trị thực của tham số m sao cho giá trị lớn số 1 của hàm số trên đoạn [1; 2] bằng 2.
Số thành phần của tập S là
A. 3
B. 1
C. 4
D. 2
Hướng dẫn giải
Chọn D
Xét hàm số
Ta có
Mặt khác
Do đó
– Trường hợp 1:
+) Với (loại)
+) Với (thỏa mãn nhu cầu)
– Trường hợp 2:
+) Với (thỏa mãn nhu cầu)
+) Với (loại)
Vậy có hai giá trị của m thỏa mãn nhu cầu.
Bài tập 3. Gọi S là tập những giá trị nguyên của tham số m sao cho giá trị lớn số 1 của hàm số f(x) = |¼ x4 – 14×2 + 48x + m – 30| trên đoạn [0; 2] không vượt quá 30. Tổng những thành phần của S bằng
A. 108
B. 120
C. 210
D. 136
Hướng dẫn giải
Chọn D
Xét hàm số g(x) = ¼ x4 – 14×2 + 48x + m – 30 trên đoạn [0; 2]
Ta có g’(x) = x3 – 28x + 48 ⇒ g’(x) = 0 ⇔
Để
⇒ m ∈ 0; 1; 2; …; 15; 16
Tổng những thành phần của S là 136.
Bài tập 4. Biết giá trị lớn số 1 của hàm số bằng 18.
Mệnh đề nào sau này đúng?
A. 0 < m < 5
B. 10 < m < 15
C. 5 < m < 10
D. 15 < m < 20
Hướng dẫn giải
Chọn D
Xét hàm số liên tục trên tập xác lập [-2; 2]
Ta có
Do đó khi x = -2, suy ra giá trị lớn số 1 của hàm số bằng
Theo bài ra = 18 ⇔ m = 15,5. Vậy 15 < m < 20
Dạng 4: Tìm Đk tham số để GTLN của hàm số y = |f(x) + g(m)| trên đoạn [a; b] đạt GTNN
Phương pháp giải
Thực hiện tiến trình sau
– Bước 1. Tìm
– Bước 2. Gọi M là giá trị lớn số 1 của số y = |f(x) + g(m)| thì
M = maxβ + g(m)≥
Dấu bằng xẩy ra khi và chỉ khi |α + g(m)| = |β + g(m)|
Áp dụng bất đẳng thức
Dấu bằng xẩy ra khi và chỉ khi [α + g(m)]․[β + g(m)] ≥ 0
– Bước 3. Kết luận khi
Bài tập mẫuBài tập 1: Biết rằng giá trị lớn số 1 của hàm số y = |x2 + 2x + m – 4| trên đoạn [-2; 1] đạt giá trị nhỏ nhất, giá trị của tham số m bằng
A. 1
B. 3
C. 4
D. 5
Hướng dẫn giải
Chọn B
Đặt f(x) = x2 + 2x
Ta có f’(x) = 2x + 2
f’(x) = 0 ⇔ x = -1 ∈ [-2; 1]
f (-2) = 0; f (1) = 3; f (-1) = -1
Do đó
Suy ra
Dấu bằng xẩy ra khi và chỉ khi
⇒ m = 3 (thỏa mãn nhu cầu)
Bài tập 2: Để giá trị lớn số 1 của hàm số đạt giá trị nhỏ nhất thì m bằng
A.
B.
C.
D.
Hướng dẫn giải
Chọn A
Tập xác lập D = [0; 2]
Đặt , x ∈ D
Ta có ⇒ f’(x) = 0 ⇔ x = 1
f (0) = 0; f (2) = 0; f (1) = 1
Suy ra
Dấu bằng xẩy ra ⇔ (thỏa mãn nhu cầu)
Suy ra giá trị lớn số 1 của hàm số là nhỏ nhất lúc
Bài tập 3. Giá trị nhỏ nhất của hàm số y = f (x, m) = |x2 – 2x + 5| + mx đạt giá trị lớn số 1 bằng
A. 2
B. 5
C. 8
D. 9
Hướng dẫn giải
Chọn B
Ta có min f (x, m) ≤ f (0, m) = 5, ∀ m ∈ ℝ
Xét m = 2 ta có f (x, 2) = |x2 – 2x + 5| + 2x ≥ x2 – 2x + 5 + 2x ≥ 5, ∀ x ∈ ℝ
Dấu bằng xẩy ra tại x = 0. Suy ra min f (x, 2) = 5, ∀ x ∈ ℝ
Do đó ⇒ max (min f (x, m)) = 5, đạt được khi m = 2
Tổng quát: y = |ax2 + bx + c| + mx
Trường hợp 1: a․c > 0 ⇒ max (miny) = c
Đạt được khi m = -b
Bài tập 4. Giá trị nhỏ nhất của hàm số f (x, m) = |x2 – 4x – 7| đạt giá trị lớn số 1 bằng
A. 7
B. -7
C. 0
D. 4
Hướng dẫn giải
Chọn C
Phương trình x2 – 4x – 7 luôn có hai nghiệm trái dấu x1 < 0 < x2
– Trường hợp 1: Nếu m ≥ 0
Ta có min f (x, m) ≤ f (x1, m) = mx1 ≤ 0, ∀ m ∈ ℝ
Xét m = 0 ta có f (x, 0) = |x2 – 4x – 7| ≥ 0, ∀ x ∈ ℝ
Dấu bằng xẩy ra tại x = x1, 2. Suy ra min f (x, m) = 0, ∀ x ∈ ℝ
Do đó ⇒ max (min f (x, m)) = 0, đạt được khi m = 0
– Trường hợp 2: Nếu m < 0
Ta có min f (x, m) ≤ f (x2, m) = mx2 < 0, ∀ m ∈ ℝ ⇒ max (min f (x, m)) < 0
So sánh cả hai trường hợp thì max (min f (x, m)) = 0 khi m = 0
Trường hợp 2: a․c < 0 ⇒ max (miny) = 0
Đạt được khi m = 0
Dạng 5: Tìm giá trị lớn số 1 giá trị nhỏ nhất lúc cho đồ thị hoặc bảng biến thiên
Bài tập 1. Hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như hình phía dưới
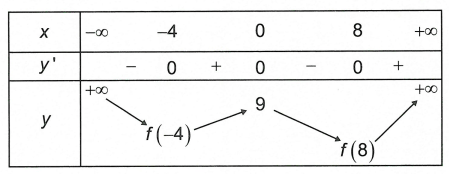
Biết f (-4) > f (8), khi đó giá trị nhỏ nhất của hàm số đã cho trên ℝ bằng
A. 9
B. f (-4)
C. f (8)
D. -4
Hướng dẫn giải
Chọn C
Từ bảng biến thiên ta có f(x) ≥ f (-4) ∀ m ∈ (-∞; 0] và f(x) ≥ f (8), ∀ m ∈ (0; +∞)
Mặt khác f (-4) > f (8) suy ra x ∈ (-∞; +∞) thì f(x) ≥ f (8)
Vậy
Bài tập 2. Cho hàm số y = f(x) xác lập trên tập hợp và có bảng biến thiên như sau
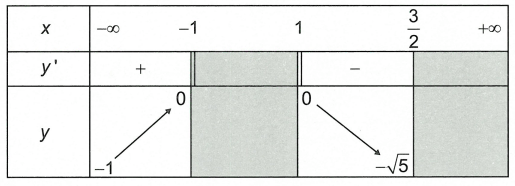
Khẳng định đúng là
A. ; không tồn tại
B. ;
C. ;
D. ; không tồn tại
Hướng dẫn giải
Chọn B
Dựa vào bảng biến thiên thì
Bài tập 3. Cho hàm số y = f(x) liên tục trên đoạn [-1; 3] và có đồ thị như hình vẽ phía dưới.
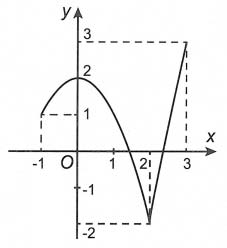
Gọi M và m lần lượt là giá trị lớn số 1 và nhỏ nhất của hàm số đã cho trên đoạn [-1; 3]. Giá trị của M – m bằng
A. 1
B. 3
C. 4
D. 5
Hướng dẫn giải
Chọn D
Dựa vào đồ thị suy ra
M = f (3) = 3; m = f (2) = -2
Vậy M – m = 5
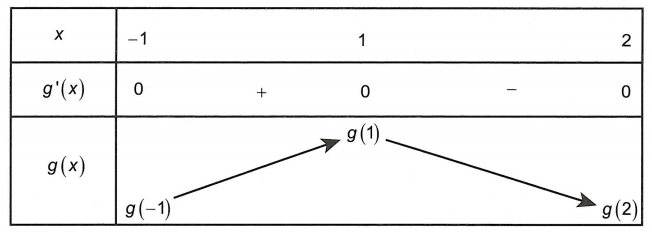
Bài tập 4. Cho đồ thị hàm số y = f’(x) như hình vẽ
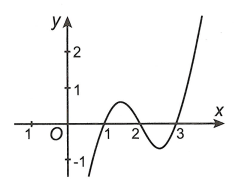
Hàm số y = f(x) đạt giá trị lớn số 1 trên khoảng chừng [1; 3] tại x0. Khi đó giá trị của x02 – 2×0 + 2022 bằng bao nhiêu?
A. 2022
B. 2022
C. 2022
D. 2022
Hướng dẫn giải
Chọn B
Dựa vào đồ thị của hàm số y = f’(x) ta có bảng biến thiên như sau
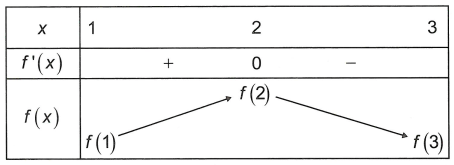
Dựa vào bảng biến thiên suy ra hàm số y = f(x) đạt giá trị lớn số 1 trên khoảng chừng [1; 3] tại x0 = 2
Vậy x02 – 2×0 + 2022 = 2022
Dạng 6. Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số lượng giác
Phương pháp giải
Ghi nhớ: Điều kiện của những ẩn phụ
– Nếu ⇒ -1 ≤ t ≤ 1
– Nếu ⇒ 0 ≤ t ≤ 1
– Nếu ⇒ 0 ≤ t ≤ 1
Nếu t = sinx ± cosx =
Bài tập mẫuBài tập 1. Giá trị lớn số 1 M và giá trị nhỏ nhất m của hàm số y = 2cos2x + 2sinx là
A. ; m = -4
B. M = 4; m = 0
C. M = 0;
D. M = 4;
Hướng dẫn giải
Chọn A
Ta có y = 2cos2x + 2sinx = 2(1 – 2sin2x) + 2sinx = -4sin2x + 2sinx + 2
Đặt t = sin x, t ∈ [-1; 1], ta được y = -4t2 + 2t +2
Ta có y’ = 0 ⇔ -8t + 2 = 0 ⇔ t = ¼ ∈ (-1; 1)
Vì nên
; m = -4
Bài tập 2. Tổng giá trị lớn số 1 và giá trị nhỏ nhất của hàm số bằng
A.
B.
C.
D. 3
Hướng dẫn giải
Chọn B
Đặt t = |cosx| ⇒ 0 ≤ t ≤ 1, ta được với 0 ≤ t ≤ 1
Vì , ∀ t ∈ [0; 1] nên
Suy ra tổng mức lớn số 1 và giá trị nhỏ nhất của hàm số đã cho bằng
Bài tập 3. Giá trị lớn số 1 M của hàm số là
A.
B. M = 3
C.
D.
Hướng dẫn giải
Chọn A
Đặt t = cos2x ⇒ 0 ≤ t ≤ 1, ta được với t ∈ [0; 1]
Ta có
Vì nên
Bài tập 4. Cho hàm số (với m là tham số thực). Giá trị lớn số 1 của hàm số đạt giá trị nhỏ nhất lúc m bằng
A.
B.
C.
D.
Hướng dẫn giải
Chọn A
Xét
Đặt t = sinx ⇒ -1 ≤ t ≤ 1, ta được với t ∈ [-1; 1]
Ta có
Vì nên
Hay
Mặt khác
Do đó
Dấu bằng đạt được khi
Bài tập 5. Giá trị nhỏ nhất của biểu thức P = |1 + 2cosx| + |1 + 2sinx| bằng
A.
B.
C. 1
D.
Hướng dẫn giải
Chọn B
Ta có P2 = 6 + 4(sinx + cosx) + 2|1 + 2(sinx + cosx) + 4sinx․cosx|
Đặt t = sinx + cosx = với
Xét y = P2 = 6 + 4t + 2 |2t2 + 2t – 1| =
Bảng biến thiên
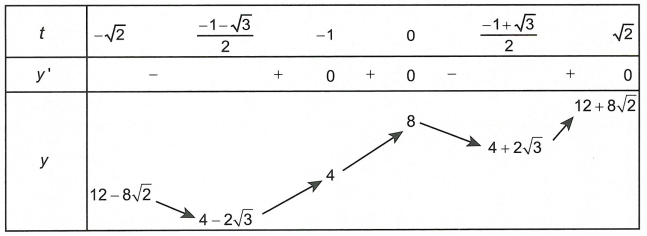
Dựa vào bảng biến thiên, suy ra
Bài tập 6. Giá trị lớn số 1 của hàm số f(x) = sinx + cos2x trên đoạn [0; π] là
A.
B.
C.
D.
Hướng dẫn giải
Chọn D
Đặt t = sinx ⇒ cos2x = 1 – 2sin2x = 1 – 2t2 , với x ∈ [0; π] ⇒ t ∈ [0; 1]
Ta được f(t) = -2t2 + t + 1 với t ∈ [0; 1]
Ta có f’(t) = -4t + 1 = 0 ⇔ t = ¼ ∈ (0; 1)
Do f (0) = 1; ; f (1) = 0 nên
Vậy giá trị lớn số 1 của hàm số là
Dạng 7. Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số khác
Bài tập 1. Giá trị lớn số 1 của hàm số bằng
A.
B. -5
C.
D. 3
Hướng dẫn giải
Chọn A
Do
Đặt
Khi đó y = 4t3 + 6t – 1 với t ∈
Vì y’ = 12t2 + 6 > 0, ∀ t nên hàm số đồng biến trên
Do đó
Bài tập 2. Giá trị lớn số 1, giá trị nhỏ nhất của hàm số lần lượt là
A. 2;
B. 4; 2
C. 4;
D. 4;
Hướng dẫn giải
Chọn D
Tập xác lập D = [1; 9]
Ta có ⇒ x = 5 ∈ (1; 9)
Vì y (1) = y (9) = ; y (5) = 4 nên max y = 4; min y =
.
Nhận xét: với hàm số (-a ≤ x ≤ b; a + b ≥ 0) thì
Suy ra dấu bằng luôn xẩy ra.
Bài tập 3. Giá trị nhỏ nhất của hàm số bằng
A.
B. -2
C. -4
D. 2
Hướng dẫn giải
Chọn A
Tập xác lập của hàm số là D = [-1; 3]
Đặt
Do , ∀ x ∈ [-1; 3], từ đó suy ra -2 ≤ t ≤ 2
Bài toán quy về tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số trên đoạn [-2; 2].
Ta có g’(t) = t + 1 = 0 ⇔ t = -1 ∈ (-2; 2)
Lại có g (-2) = -2; g (2) = 2; g (-1) =
Suy ra giá trị nhỏ nhất bằng
Nhận xét: Với hàm số (-a ≤ x ≤ b; a + b ≥ 0) thì
Dạng 8. Tìm giá trị lớn số 1, giá trị nhỏ nhất của biểu thức nhiều biến
Bài tập 1. Cho biểu thức với x2 + y2 ≠ 0. Giá trị nhỏ nhất của P bằng
A. 3
B.
C. 1
D. 4
Hướng dẫn giải
Chọn B.
Nếu y = 0 thì P = 1 (1)
Nếu y ≠ 0 thì
Đặt , khi đó
Bảng biến thiên
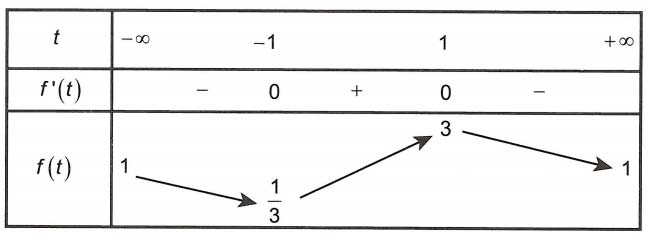
Dựa vào bảng biến thiên ta có P = f(t) ≥ (2)
Từ (1) và (2) suy ra có P = f(t) ≥ ⇒ min P =
Bài tập 2. Cho hai số thực x, y thỏa mãn nhu cầu x ≥ 0, y ≥ 0 và x + y = 1. Giá trị nhỏ nhất và giá trị lớn số 1 của biểu thức lần lượt là
A. và 1
B. 0 và 1
C. và 1
D. 1 và 2
Hướng dẫn giải
Chọn C
Ta có
Đặt t = xy ta được
Vì x ≥ 0, y ≥ 0 ⇒ t ≥ 0
Mặt khác
Khi đó, bài toán trở thành tìm giá trị lớn số 1 của hàm số trên
Xét hàm số xác lập và liên tục trên
Ta có với ∀ t ∈
⇒ Hàm số g(t) nghịch biến trên đoạn
Do đó
Bài tập 3. Cho x, y là những số thực thỏa mãn (x – 3)2 + (y – 1)2 = 5. Giá trị nhỏ nhất của biểu thức bằng
A. 3
B.
C.
D.
Hướng dẫn giải
Chọn A
(x – 3)2 + (y – 1)2 = 5 ⇒ x2 + y2 – 6x – 2y + 5 = 0
Đặt t = x + 2y
(12 + 22)․[(x – 3)2 + (y – 1)2] ≥ [(x – 3) + (2y – 2)]2
Ta được
Xét
Vì f (0) = 4; f (10) = ; f (1) = 3 ⇒ min P = 3 khi t = 1.
Bài tập 4. Gọi x0, y0, z0 là ba số thực dương sao cho biểu thức đạt giá trị nhỏ nhất.
Tổng x0 + y0 + z0 bằng
A. 3
B. 1
C.
D.
Hướng dẫn giải
Chọn B
Ta có
Đặt x + y + x = t. Khi đó
Ta có
Bảng biến thiên
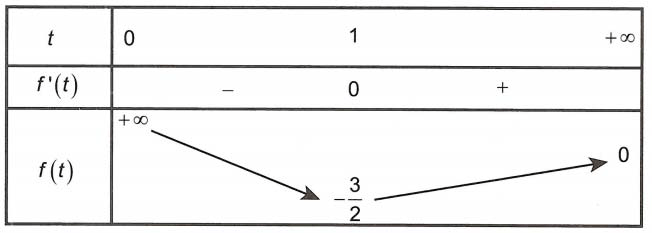
Suy ra . Dấu “=” xẩy ra
Do đó
Bài tập 5. Cho x,y là những số thực dương thỏa mãn nhu cầu Đk . Tổng giá trị lớn số 1 và nhỏ nhất của biểu thức P = 3x2y – xy2 – 2×3 + 2x bằng
A. 8
B. 0
C. 12
D. 4
Hướng dẫn giải
Chọn B
Với Đk bài toán x, y > 0 và x2 – xy + 3 = 0
Lại có
Từ đó
Xét hàm số
Suy ra hàm số đồng biến trên
⇒ f (1) ≤ f(x) ≤ ⇒ -4 ≤ f(x) ≤ 4 ⇒ max P + min P = 4 + (-4) = 0
Bài tập 6. Cho x, y, z là ba số thực thuộc đoạn [1; 9] và x ≥ y, x ≥ z. Giá trị nhỏ nhất của biểu thức bằng
A.
B.
C.
D. 1
Hướng dẫn giải
Chọn C
Thật vậy đúng do ab ≥ 1
Dấu bằng xẩy ra khi và chỉ khi a = b hoặc ab = 1.
Áp dụng bất đẳng thức trên
Đặt . Xét hàm số
trên đoạn [1; 3]
f’(t) = 0 ⇔ t4 – 2t3 – 24t2 – 2t + 100 = 0
⇔ (t – 2)(t3 – 24t – 50) = 0 ⇔ t = 2 do t3 – 24t – 50 < 0, ∀ x ∈ [1; 3]
Bảng biến thiên
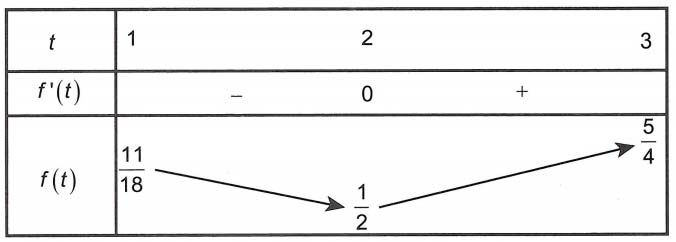
Suy ra khi và chỉ khi
Dạng 9. Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số y = f(u(x)), y = f(u(x)) ± h(x)… lúc biết bảng biến thiên hoặc đồ thị của hàm số y = f(x).
Phương pháp
Thực hiện theo một trong hai cách
Cách 1:
Bước 1. Đặt t = u(x).
Đánh giá giá trị của t trên khoảng chừng K.
Chú ý: Có thể sử dụng khảo sát hàm số, bất đẳng thức để xem nhận giá trị của t = u(x).
– Bước 2. Từ bảng biến thiên hoặc đồ thị của hàm số cho ta giá trị lớn số 1 và giá trị nhỏ nhất của hàm số y = f(t).
– Bước 3. Kết luận.
Cách 2:
– Bước 1. Tính đạo hàm y’ = u’(x)․f’(u(x)).
– Bước 2. Tìm nghiệm y’ = u’(x)․f’(u(x)) = 0
– Bước 3. Lập bảng biến thiên
– Bước 4. Kết luận về giá trị lớn số 1, giá trị nhỏ nhất của hàm số y = f(x), y = f(u(x)), y = f(u(x)) ± h(x)…
Bài tập mẫuBài tập 1. Cho hàm số y = f(x) có bảng biến thiên như sau
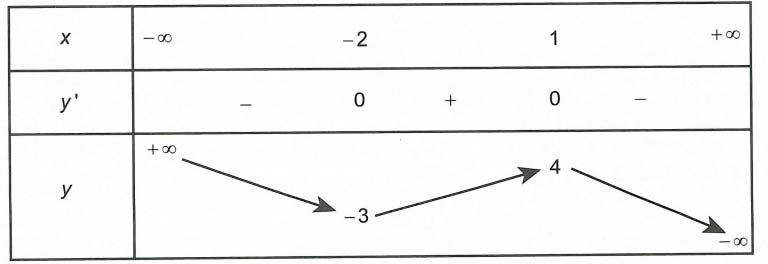
Hàm số y = f (|x – 1|) có mức giá trị nhỏ nhất trên đoạn [0; 2] bằng
A. f (-2)
B. f (2)
C. f (1)
D. f (0)
Hướng dẫn giải
Chọn D
Đặt t =|x – 1|, ∀ x ∈ [0; 2] ⇒ t ∈ [0; 1]
Dựa vào bảng biến thiên ta có hàm số y = f(t) có mức giá trị nhỏ nhất
Bài tập 2. Cho hàm số y = f(x) có đồ thị như hình vẽ sau. Khi đó hàm số y = f (2 – x2) đạt giá trị nhỏ nhất trên bằng
A. f (-2)
B. f (2)
C. f (1)
D. f (0)
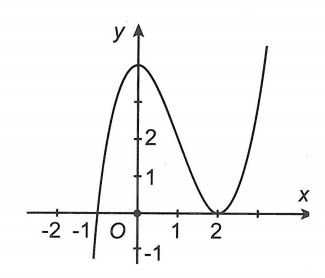
Hướng dẫn giải
Chọn B
Đặt t = 2 – x2. Từ x ∈ ⇔ 0 ≤ x2 ≤ 2 ⇔ 2 ≥ 2 – x2 ≥ 0 ⇒ t ∈ [0; 2]
Dựa vào đồ thị, hàm số y = f(t) có mức giá trị nhỏ nhất
Bài tập 3. Cho hàm số y = f(x) = ax4 + bx2 + c xác lập và liên tục trên ℝ và có bảng biến thiên sau
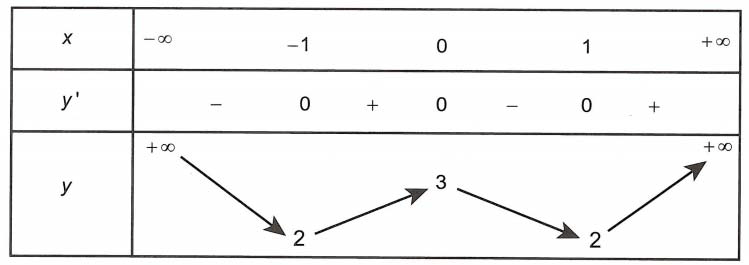
Giá trị nhỏ nhất của hàm số y = f (x + 3) trên đoạn [0; 2] là
A. 64
B. 65
C. 66
D. 67
Hướng dẫn giải
Chọn C
Hàm số có dạng f(x) = ax4 + bx2 + c. Từ bảng biến thiên ta có
⇒ f(x) = x4 – 2×2 + 3
Đặt t = x + 3, x ∈ [0; 2] ⇒ t ∈ [3; 5]
Dựa vào đồ thị, hàm số y = f(t) đồng biến trên đoạn [3;5].
Do đó
Dạng 10. Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số y = f(u(x)), y = f(u(x)) ± h(x)… Khi biết đồ thị của hàm số y = f’(x)
Bài tập 1. Cho hàm số y = f(x) có đạo hàm và liên tục trên ℝ. Biết rằng đồ thị hàm số y = f’(x) như dưới đây.
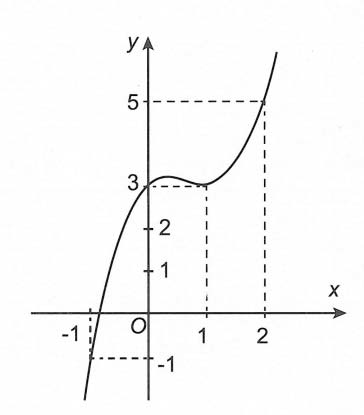
Lập hàm số g(x) = f(x) – x2 – x.
Mệnh đề nào sau này đúng?
A. g(-1) > g(1)
B. g(-1) = g(1)
C. g(1) = g(2)
D. g(1) > g(2)
Hướng dẫn giải
Chọn D
Ta có g’(x) = f’(x) – 2x – 1
Từ đồ thị hàm số y = f’(x) và đường thẳng y = 2x + 1 ta có g’(x) = 0
⇔ f’(x) = 2x + 1 ⇒
Bảng biến thiên
Ta chỉ việc so sánh trên đoạn [-1; 2]. Đường thẳng y = 2x + 1 là đường thẳng đi qua những điểm A(-1; -1), B(1; 3), C(2; 5) nên đồ thị hàm số y = f’(x) và đường thẳng y = 2x + 1 cắt nhau tại 3 điểm.
Dạng 11. Ứng dụng của giá trị lớn số 1 và nhỏ nhất trong những bài toán thực tiễn
Bài tập 1. Một chất điểm hoạt động và sinh hoạt giải trí theo quy luật s = 3t2 – t3. Thời điểm t (giây) mà tại đó vận tốc v (m/s) của chất điểm hoạt động và sinh hoạt giải trí đạt giá trị lớn số 1 là
A. t = 2s
B. t = 5s
C. t = 1s
D. t =3s
Hướng dẫn giải
Chọn C
Ta có v(t) = s’(t) = 6t – 3t2 ⇒ v(t) = -3(t – 1)2 + 3 ≤ 3, ∀ t ∈ ℝ
Giá trị lớn số 1 của v(t) = 3 khi t = 1.
Bài tập 2. Một vật hoạt động và sinh hoạt giải trí theo quy luật s = -⅓t3 + 6t2 với t (giây) là khoảng chừng thời hạn tính từ khi vật khởi đầu hoạt động và sinh hoạt giải trí và s (mét) là quãng đường vật di tán được trong mức chừng thời hạn đó. Hỏi trong mức chừng thời hạn 7 giây, Tính từ lúc lúc khởi đầu hoạt động và sinh hoạt giải trí, vận tốc lớn số 1 của vật đạt được bằng bao nhiêu?
A. 180 (m/s)
B. 36 (m/s)
C. 144 (m/s)
D. 24 (m/s)
Hướng dẫn giải
Chọn B
Ta có v(t) = s’(t) = -t2 + 12t
v’(t) = -2t + 12 = 0 ⇔ t = 6
Vì v (6) = 36; v (0) = 0; v (7) = 35 nên vận tốc lớn số 1 đạt được bằng 36 (m/s).
Bài tập 3. Một loại thuốc được sử dụng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào khung hình trong t giờ được cho bởi công thức (mg/L). Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
A. 4 giờ
B. 1 giờ
C. 3 giờ
D. 2 giờ
Hướng dẫn giải
Chọn B
Xét hàm số (t > 0)
Bảng biến thiên
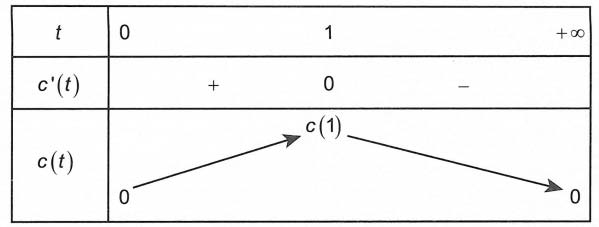
Với t = 1 (giờ) thì nồng độ thuốc trong máu của bệnh nhân cao nhất.
Bài tập 4. Người ta xây một bể chứa nước với dạng khối hộp chữ nhật không nắp hoàn toàn có thể tích bằng m3. Đáy bể là hình chữ nhật có chiều dài gấp hai chiều rộng. Giá thuê nhân công để xây bể là 600.000 đồng/ mét vuông. Hãy xác lập kích thước của bể sao cho ngân sách thuê nhân công thấp nhất. Chi phí đó là:
A. 75 triệu đồng
B. 85 triệu đồng
C. 90 triệu đồng
D. 95 triệu đồng
Hướng dẫn giải
Chọn C
Gọi x (m) là chiều rộng của đáy bể, khi đó chiều dài của đáy bể là 2x (m) và h (m) là độ cao bể
Bể hoàn toàn có thể tích bằng
Diện tích cần xây
Xét hàm
Bảng biến thiên
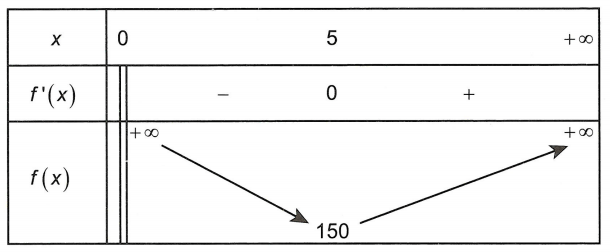
Do đó
Chi phí thuê nhân công thấp nhất lúc diện tích s quy hoạnh xây dựng là nhỏ nhất và bằng Smin = 150 Vậy giá thuê nhân công thấp nhất là 150 × 600.000 = 90.000.000 đồng.
Bài tập 5. Bác Hoàng có một tấm thép mỏng dính hình tròn trụ, tâm O, bán kính 4 dm. Bác định cắt ra một hình quạt tròn tâm O, quấn rồi hàn ghép hai mép của hình quạt tròn lại để tạo thành một dụng cụ dạng mặt nón tròn xoay (tìm hiểu thêm hình vẽ). Dung tích lớn số 1 hoàn toàn có thể của dụng cụ mà bác Hoàng tạo ra bằng bao nhiêu? (bỏ qua phần mối hàn và độ dày của tấm thép)
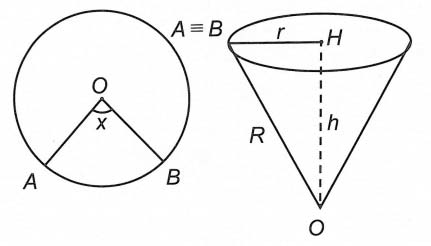
A.
B.
C.
D.
Hướng dẫn giải
Chọn A
Khi hàn hai mép của hình quạt tròn, độ dài đường sinh của hình nón bằng bán kính của hình quạt tròn, tức là OA = 4dm
Thể tích của hình nón với 0 < h < 4
Ta có
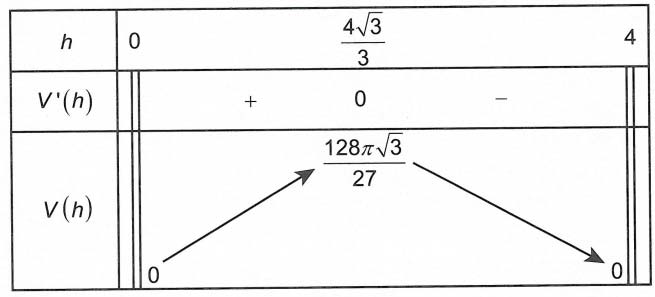
Dựa vào bảng biến thiên, suy ra thể tích lớn số 1 của hình nón là
Bài tập 6. Người ta làm chiếc thùng phi dạng hình trụ, kín hai đáy, với thể tích theo yêu cầu là 2πm3. Hỏi bán kính đáy R và độ cao h của thùng phi bằng bao nhiêu để khi làm thì tiết kiệm chi phí vật tư nhất
A. ; h = 8m
B. R = 1m; h = 2m
C. R = 2m;
D. R = 4m;
Hướng dẫn giải
Chọn B
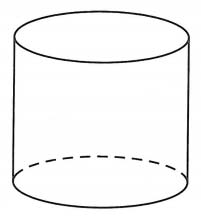
Từ giả thiết ta có
Diện tích toàn phần của thùng phi là
Xét hàm số với R ∈ (0; +∞)
Ta có
f’(R) = 0 ⇔ R = 1
Bảng biến thiên
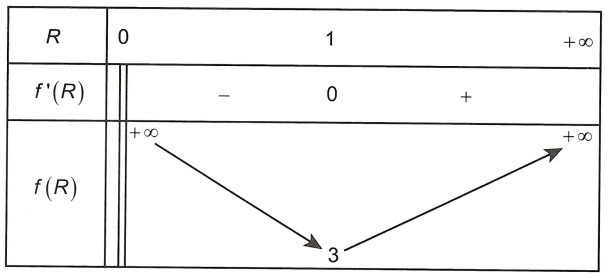
Suy ra diện tích s quy hoạnh toàn phần đạt giá trị nhỏ nhất lúc R = 1 ⇒ h = 2
Vậy để tiết kiệm chi phí vật tư nhất lúc làm thùng phi thì R = 1m; h = 2m
Bài tập 7. Một đường dây điện được nối từ một nhà máy sản xuất điện ở A đến một quần hòn đảo ở C như hình vẽ. Khoảng cách từ C đến B là một trong km. Bờ biển chạy thẳng từ A đến B với mức chừng cách là 4km. Tổng ngân sách lắp đặt cho 1km dây điện trên biển khơi là 40 triệu đồng, còn trên đất liền là 20 triệu đồng. Tính tổng ngân sách nhỏ nhất để hoàn thành xong việc làm trên (làm tròn đến hai chữ số sau dấu phẩy)
A. 120 triệu đồng
B. 164,92 triệu đồng
C. 114,64 triệu đồng
D. 106,25 triệu đồng
Hướng dẫn giải
Chọn C
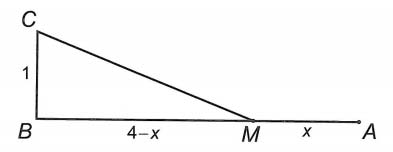
Gọi M là yếu tố trên đoạn thẳng AB để lắp đặt đường dây điện ra biển nối với điểm C
Đặt AM = x ⇒ BM = 4 – x ⇒ , x ∈ [0; 4]
Khi đó tổng ngân sách lắp đặt là (cty: triệu đồng)
Ta có
Do đó ngân sách nhỏ nhất để hoàn thành xong việc làm là 114,64 triệu đồng.
Dạng 12. Tìm m để F(x; m) = 0 có nghiệm trên tập D
Phương pháp giải
Thực hiện theo tiến trình sau
– Bước 1. Cô lập tham số m và đưa về dạng f(x) = g(m)
– Bước 2. Khảo sát sự biến thiên của hàm số f(x) trên D
– Bước 3. Dựa vào bảng biến thiên để xác lập giá trị tham số A(m) sao cho đường thẳng y = g(m) cắt đồ thị hàm số y = f(x)
– Bước 4. Kết luận
Chú ý:
+) Nếu hàm số y = f(x) liên tục và có mức giá trị lớn số 1 và giá trị nhỏ nhất trên D thì phương trình f(x) = g(m) có nghiệm khi và chỉ khi
+) Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ việc nhờ vào bảng biến thiên để xác lập Đk sao cho đường thẳng y = g(m) nằm ngang cắt đồ thị hàm số y = f(x) tại k điểm phân biệt.
Bài tập mẫuBài tập 1: Có bao nhiêu giá trị nguyên của tham số m trong đoạn [-100; 100] để phương trình có nghiệm thực?
A. 100
B. 101
C. 102
D. 103
Hướng dẫn giải
Chọn D
Điều kiện x ≥ -1
Đặt
Ta được phương trình 2t = t2 – 1 + m ⇔ m = -t2 + 2t + 1
Xét hàm số f(t) = -t2 + 2t + 1, t ≥ 0
f’(t) = -2t + 2 = 0 ⇔ t = 1
Bảng biến thiên
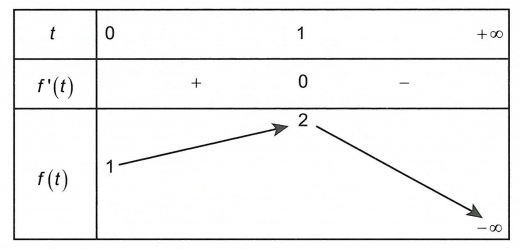
Từ bảng biến thiên suy ra phương trình đã cho có nghiệm khi m ≤ 2 ⇒ -100 ≤ m ≤ 2
Vậy có 103 giá trị nguyên m thỏa mãn nhu cầu
Bài tập 2. Cho phương trình (m là tham số). Biết rằng tập hợp những giá trị của tham số m để phương trình có nghiệm thuộc đoạn
là đoạn [a; b]. Giá trị của biểu thức T = -a + 2b là
A .T = 4
B.
C. T = 3
D.
Hướng dẫn giải
Chọn A
Đặt
Xét hàm số trên đoạn
Vì nên t ∈ [1; 3]
Yêu cầu của bài toán tương tự với phương trình m(t + 1) = t2 – 2 có nghiệm thuộc đoạn [1; 3] ⇔ có nghiệm thuộc đoạn [1; 3] (1)
Xét hàm số trên đoạn [1; 3]
, ∀ t ∈ [1; 3] khi hàm số đồng biến trên đoạn [1; 3]
Để phương trình (1) đã cho có nghiệm thì
Vậy ⇒ T = 4
Bài tập 3. Giá trị nhỏ nhất của tham số m để hệ phương trình (x, y ∈ ℝ) có nghiệm là m0. Mệnh đề nào dưới đây đúng?
A. m0 ∈ (-20; -15)
B. m0 ∈ (-12; -8)
C.
D.
Hướng dẫn giải
Chọn D
Ta có
Từ (1) suy ra y = 2 – x thay vào (2) ta được (2) ⇒ x4 + (2 – x)4 = m (3)
Xét hàm số f(x) = x4 + (2 – x)4 có tập xác lập D = ℝ
f’(x) = 4×3 – 4(2 – x)3 ⇒ f’(x) = 0 ⇔ x3 = (2 – x)3 ⇔ x = 2 – x ⇔ x = 1
Bảng biến thiên
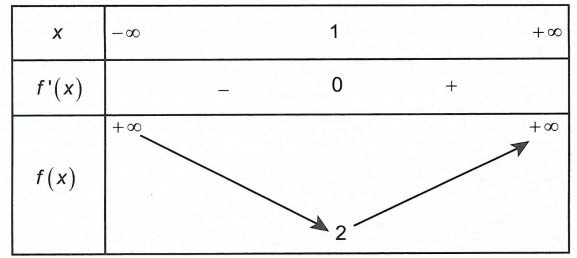
Hệ đã cho có nghiệm thực khi và chỉ khi phương trình (3) có nghiệm thực
Dựa vào bảng biến thiên ta được m ≥ 2 ⇒ m0 = 2 ⇒
Dạng 13. Tìm m để bất phương trình F(x; m) > 0; F(x; m) ≥ 0; F(x; m) < 0; F(x; m) ≤ 0 có nghiệm trên tập D.
Phương pháp giải
Thực hiện theo tiến trình sau
Chú ý: Nếu hàm số f(x) liên tục và có mức giá trị lớn số 1; giá trị nhỏ nhất trên D thì
+) Bất phương trình g(m) ≤ f(x) có nghiệm trên D ⇔ g(m) ≤ max f(x)
+) Bất phương trình g(m) ≤ f(x) nghiệm đúng ∀ x ∈ D ⇔ g(m) ≤ min f(x)
+) Bất phương trình g(m) ≥ f(x) có nghiệm trên D ⇔ g(m) ≥ min f(x)
+) Bất phương trình g(m) ≥ f(x) nghiệm đúng ∀ x ∈ D ⇔ g(m) ≥ max f(x)
Bài tập mẫuBài tập 1: Các giá trị của tham số m để bất phương trình có nghiệm trên khoảng chừng (-∞; 1) là
A. m < 5
B. m ≤ -3
C. m ≤ 1
D. m ≥ 3
Hướng dẫn giải
Chọn B
Bất phương trình đã cho tương tự với
Xét hàm số trên khoảng chừng (-∞; 1)
Bảng biến thiên
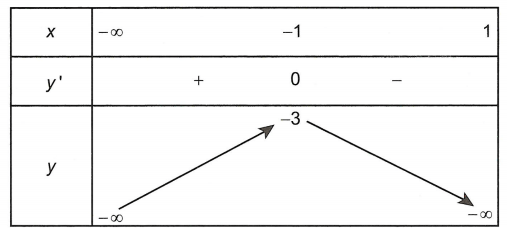
Từ bảng biến thiên, để bất phương trình có nghiệm trên khoảng chừng (-∞; 1) thì m ≤ -3
Bài tập 2. Gọi S là tập hợp những giá trị nguyên của tham số m ∈ [0; 2019] để bất phương trình nghiệm đúng với mọi x ∈ [-1;1]. Số những thành phần của tập S là
A. 1
B. 2022
C. 2022
D. 2
Hướng dẫn giải
Chọn C
Đặt , với x ∈ [-1;1] ⇒ t ∈ [0;1]
Bất phương trình đã cho trở thành t3 – t2 + 1 – m ≤ 0 ⇔ m ≥ t3 – t2 + 1 (1)
Yêu cầu của bài toán tương tự với bất phương trình (1) nghiệm đúng với mọi t ∈ [0;1]
Xét hàm số f(t) = t3 – t2 + 1 ⇒ f’(t) = 3t2 – 2t
f’(t) = 0 ⇔
Vì f (0) = f (1) = 1; nên
Do đó bất phương trình (1) nghiệm đúng với mọi t ∈ [0;1] khi và chỉ khi m ≥ 1
Mặt khác m là số nguyên thuộc [0; 2019] nên m ∈ 1; 2; 3; …; 2022
Vậy có 2022 giá trị của m thỏa mãn nhu cầu bài toán.
Bài tập 3. Cho hàm số y = f(x) liên tục trên [-1; 3] và có đồ thị như hình vẽ.
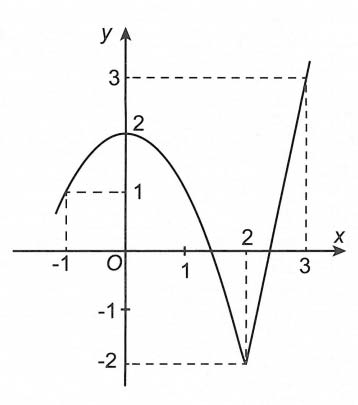
Bất phương trình có nghiệm thuộc [-1; 3] khi và chỉ khi
A. m ≤ 7
B. m ≥ 7
C.
D.
Hướng dẫn giải
Chọn A
Xét hàm số trên đoạn [-1; 3]
Ta có
Dấu bằng xẩy ra khi x = 3
Suy ra tại x = 3 (1)
Mặt khác nhờ vào đồ thị của f(x) ta có tại x = 3 (2)
Từ (1) và (2) suy ra tại x = 3
Vậy bất phương trình có nghiệm thuộc [-1; 3] khi và chỉ khi
⇔ m ≤ 7
Tài liệu tìm GTLN GTNN của hàm số
Bộ tài liệu về tìm giá trị lớn số 1 nhỏ nhất của hàm số cực hay giúp bạn nắm vững chuyên đề này và tiếp xúc với nhiều dạng bài nhất hoàn toàn có thể. Hãy tìm một tài liệu phù phù thích hợp với bản thân và nghiên cứu và phân tích.
#1. Các dạng toán GTLN GTNN thường gặp trong kỳ thi THPT QG
tin tức tài liệuTác giảThầy Nguyễn Bảo VươngSố trang66Lời giải chi tiếtCó
Mục lục tài liệu:
– Dạng 1. Xác định giá trị lớn số 1 – giá trị nhỏ nhất của hàm số thông qua đồ thị của nó.
– Dạng 2. Xác định giá trị lớn số 1 – giá trị nhỏ nhất của hàm số trên đoạn [a;b].
– Dạng 3. Xác định giá trị lớn số 1 – giá trị nhỏ nhất của hàm số trên khoảng chừng (a;b).
– Dạng 4. Ứng dụng GTLN-GTNN vào bài toán thực tiễn.
– Dạng 5. Định m để GTLN-GTNN của hàm số thỏa mãn nhu cầu Đk cho trước.
– Dạng 6. Bài toán GTLN-GTNN liên quan đến đồ thị đạo hàm.
– Dạng 7. Ứng dụng GTLN-GTNN vào bài toán đại số.
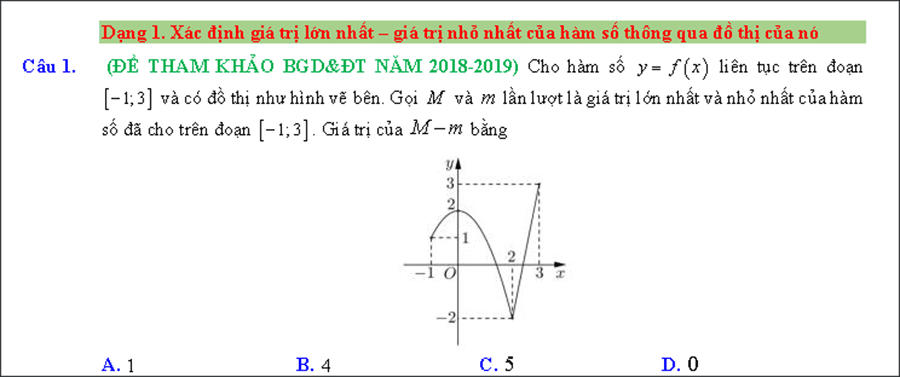
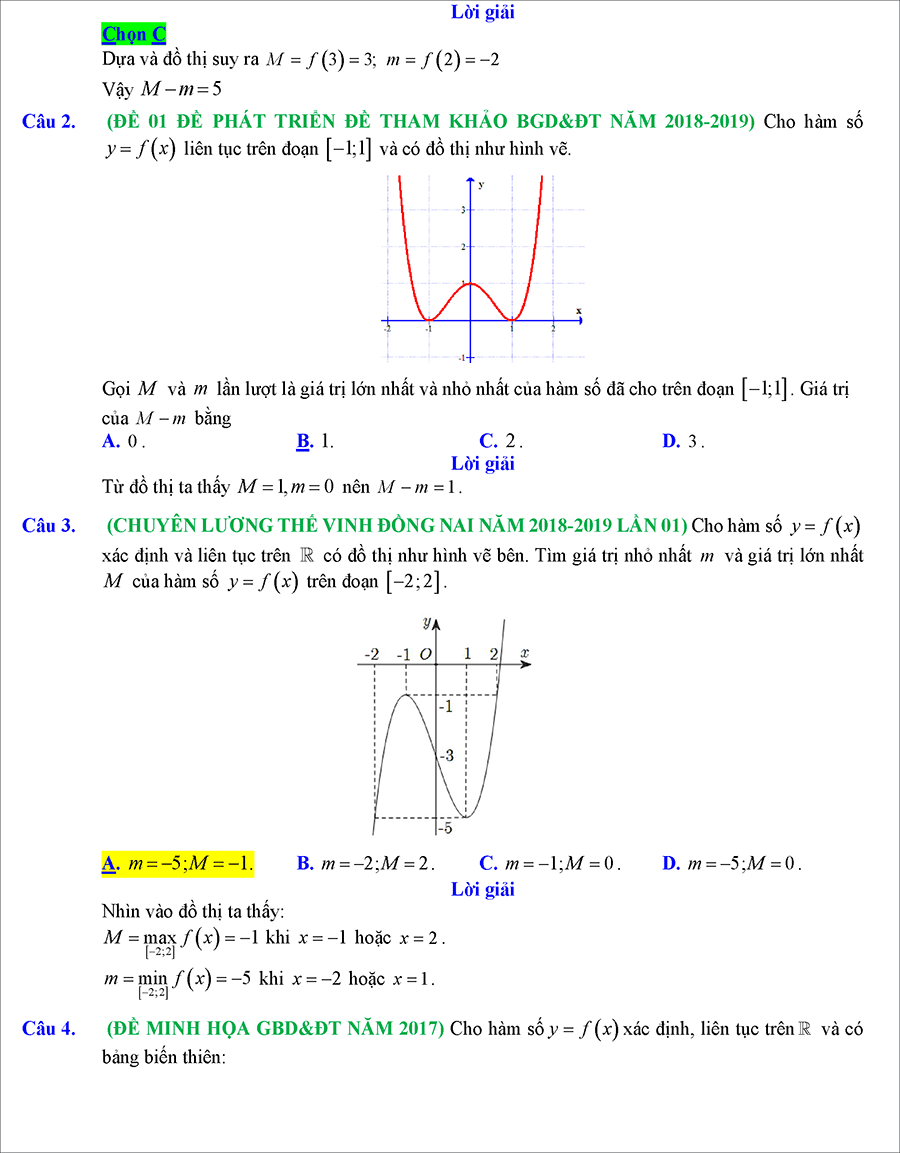
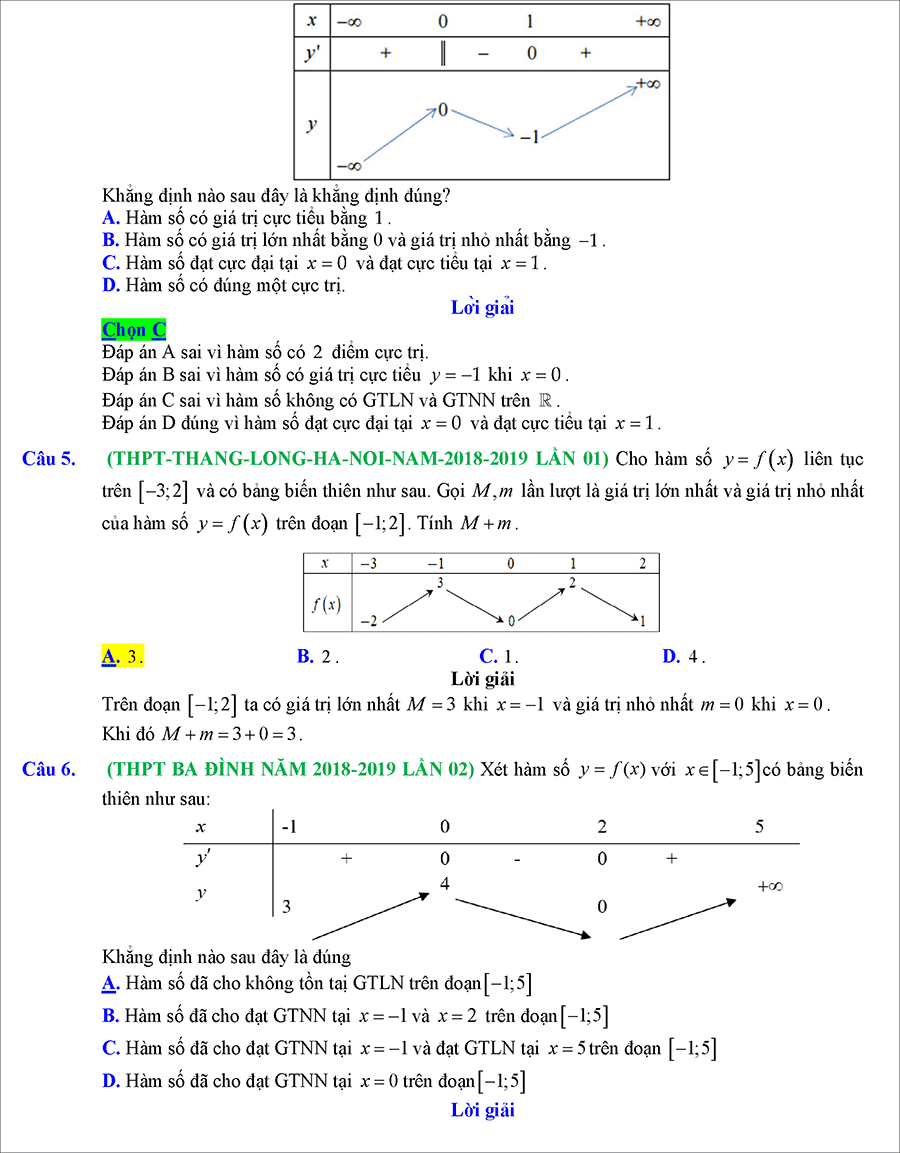
#2. Bài tập GTLN GTNN của hàm số
tin tức tài liệuTác giảThầy Lê Bá BảoSố trang71Lời giải chi tiếtCó
Mục lục tài liệu:
– Dạng toán 1: Tìm GTLN GTNN trên khoảng chừng (nửa khoảng chừng – đoạn)
– Dạng toán 2: Max min hàm nhiều biến
– Dạng toán 3: Bài toán thực tiễn – tối ưu
– Dạng toán 4: Phương trình – bất phương trình
– Dạng toán 5: Bài toán tham số
#3. Bài tập vận dụng cao GTLN GTNN của hàm số
tin tức tài liệuTác giảGiáo viên THPT Đầm DơiSố trang130Lời giải chi tiếtCó
Mục lục tài liệu:
– Dạng 1: Tìm GTLN GTNN của hàm số theo công thức
– Dạng 2: Tìm GTLN GTNN của hàm nhiều biến
– Dạng 3: Bài toán ứng dụng
– Dạng 4: Ứng dụng GTLN GTNN vào tìm số nghiệm của phương trình và bất phương trình

#4. Tổng ôn trắc nghiệm GTLN GTNN của hàm số
tin tức tài liệuTác giảThầy Nguyễn VươngSố trang82Lời giải chi tiếtCó
Mục lục tài liệu:
– Tìm giá trị lớn số 1 và giá trị nhỏ nhất của hàm số.
– Tìm m để GTLN GTNN thỏa mãn nhu cầu Đk K nào đó.
– Giá trị lớn số 1 giá trị nhỏ nhất của hàm số chứa dấu giá trị tuyệt đối (Bài toán chứa tham số).
– Giá trị lớn số 1 – giá trị nhỏ nhất hàm ẩn, hàm hợp.
– Ứng dụng GTLN – GTNN giải bài toán thực tiễn.


#5. GTLN GTNN của hàm giá trị tuyệt đối
tin tức tài liệuTác giảThầy Trần Minh NgọcSố trang17Lời giải chi tiếtCó
Mục lục tài liệu:
Trong đề tìm hiểu thêm của Bộ GD lần 1 và lần 2, cũng như đề thi thử của những sở giáo dục, những trường phổ thông năm 2022 thường có bài toán liên quan đến GTLN-GTNN của hàm số chứa dấu trị tuyệt đối. Để xử lý và xử lý được những dạng toán này những em cần ghi nhớ bài toán tổng quát trong tài liệu.




#6. Bài tập GTLN GTNN của hàm số
tin tức tài liệuTác giảTrung tâm luyện thi Đại Học AmsterdamSố trang65Lời giải chi tiếtCó
Mục lục tài liệu:
– Lý thuyết giá trị lớn số 1 nhỏ nhất của hàm số.
– Dạng 1: Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số trên đoạn [a;b].
– Dạng 2: Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số trên khoảng chừng nửa khoảng chừng.
– Dạng 3: Xác định tham số m để hàm số có mức giá trị lớn số 1, giá trị nhỏ nhất thỏa Đk cho trước.
– Dạng 4: Các bài toán thực tiễn.



#7. Tóm tắt lý thuyết và bài tập trắc nghiệp GTLN GTNN của hàm số
tin tức tài liệuTác giảSố trang35Lời giải chi tiếtCó
Mục lục tài liệu:
– Tổng hợp trắc nghiệm giá trị lớn số 1 – giá trị nhỏ nhất của hàm số
– Phần trắc nghiệm
– Phần đáp án.




#8. Các bài tập VDC GTLN và GTNN của hàm số
tin tức tài liệuTác giảSố trang36Lời giải chi tiếtCó
Mục lục tài liệu:
– Dạng 1: Tìm GTLN – GTNN của hàm số y = f(x) trên một khoảng chừng.
– Dạng 2: Tìm GTLN và GTNN của hàm số trên một đoạn.
– Dạng 3: Tìm GTLN – GTNN của hàm số y = |f(x)| trên đoạn [a; b].
– Dạng 4: Tìm Đk tham số để GTLN của hàm số y = |f(x) + g(m)| trên đoạn [a; b] đạt GTNN.
– Dạng 5: TÌM GTLN-GTNN khi cho đồ thị – bảng biến thiên.
– Dạng 6: Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số lượng giác.
– Dạng 7: Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số khác.
– Dạng 8: Tìm giá trị lớn số 1, giá trị nhỏ nhất của biểu thức nhiều biến.
– Dạng 9:Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm số y = f(u(x)),y = f(u(x))±h(x)… lúc biết bảng biến thiên hoặc đồ thị của hàm số y = f(x).
– Dạng 10: Tìm giá trị lớn số 1, giá trị nhỏ nhất của hàm hợp lúc biết đồ thị của hàm số y f ‘(x).
– Dạng 11. Ứng dụng của giá trị lớn số 1 và nhỏ nhất trong những bài toán thực tiễn.
– Dạng 12: Dạng 12. Tìm m để F (x;m) = 0 có nghiệm trên tập D.
– Dạng 13: Tìm m để bất phương trình chứa tham số m có nghiệm trên tập D.




#9. GTLN GTNN của hàm hợp hàm link
tin tức tài liệuTác giảĐặng Việt ĐôngSố trang91Lời giải chi tiếtCó
Mục lục tài liệu:
– Dạng 1: GTLN, GTNN liên quan hàm số lúc biết BBT, đồ thị
– Dạng 2: GTLN, GTNN hàm link lúc biết BBT, đồ thị
– Dạng 3: GTLN, GTNN hàm số có tham số không chứa giá tuyệt đối
– Dạng 4: GTLN, GTNN hàm trị tuyệt đối chứa tham số.




#10. GTNN GTLN của hàm số trị tuyệt đối
tin tức tài liệuTác giảSố trangLời giải rõ ràng
Mục lục tài liệu:
– Dạng 1: Tìm GTLN – GTNN thỏa mãn nhu cầu Đk rõ ràng
– Dạng 2: Tìm Đk của tham số
– Dạng 3: Bài toán max đạt min
– Dạng 4: Bài toán min đạt min
– Các bài tập vận dụng – vận dụng cao trong những đề thi






Bài viết tổng hợp rõ ràng về những dạng bài tập tìm GTLN, GTNN của hàm số. Mong rằng qua bài học kinh nghiệm tay nghề ngày hôm nay, bạn đọc hoàn toàn có thể nắm vững rõ ràng về những dạng bài tập mà VerbaLearn Math vừa trình làng. Nếu có bất kì vướng mắc gì từ bài học kinh nghiệm tay nghề, bạn hoàn toàn có thể liên hệ với chúng tôi bằng phương pháp để lại phản hồi xuống phía phía dưới nhé.
![]()
Thầy Dũng dạy toán học từ thời điểm năm 2010 sau khi nhận bằng sư phạm môn toán tại trường Đại Học Sư Phạm Thành Phố Thành Phố Đà Nẵng. Triết lý dạy học của thầy luôn coi trọng chất lượng hơn số lượng bởi ở một góc nhìn nào đó, toàn bộ chúng ta sử dụng toán học hằng ngày trong môi trường tự nhiên vạn vật thiên nhiên sống đời thường và nên phải làm rõ về bản chất của nó thay vì học sơ sài. Thầy cảm hứng rất như mong ước khi được làm sửa đổi và biên tập viên cho môn toán tại VerbaLearn, nơi mà những bài dạy của thầy hoàn toàn có thể tiếp cận nhiều học viên hơn.
Share Link Download Tìm giá trị nhỏ nhất m của hàm số f x ln x căn x 2 e 2 miễn phí
Bạn vừa tìm hiểu thêm nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Video Tìm giá trị nhỏ nhất m của hàm số f x ln x căn x 2 e 2 tiên tiến và phát triển nhất và Chia SẻLink Tải Tìm giá trị nhỏ nhất m của hàm số f x ln x căn x 2 e 2 miễn phí.

Thảo Luận vướng mắc về Tìm giá trị nhỏ nhất m của hàm số f x ln x căn x 2 e 2
Nếu sau khi đọc nội dung bài viết Tìm giá trị nhỏ nhất m của hàm số f x ln x căn x 2 e 2 vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Admin lý giải và hướng dẫn lại nha
#Tìm #giá #trị #nhỏ #nhất #của #hàm #số #căn