Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này có diện tích là Đầy đủ

Kinh Nghiệm về Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này còn có diện tích s quy hoạnh là Chi Tiết

You đang tìm kiếm từ khóa Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này còn có diện tích s quy hoạnh là được Update vào lúc : 2022-04-13 14:30:11 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.

Dù bạn muốn tính thể tích của một chiếc hộp để gửi bưu kiện hay để vượt qua bài kiểm tra sắp tới đây thì việc này cũng rất đơn thuần và giản dị. Thể tích là giá trị cho biết thêm thêm độ lớn của một vật trong không khí ba chiều, do vậy nhờ vào thể tích của chiếc hộp, bạn sẽ biết trong hộp có bao nhiêu không khí. Để tính thể tích, bạn cần thực thi một vài phép đo đơn thuần và giản dị để sở hữu chiều dài, chiều rộng, độ cao của hộp, tiếp theo đó nhân chúng lại với nhau.

Nội dung chính

• Tính thể tích hình hộp chữ nhật


• Tính thể tích hộp có những hình dạng khác


• Tính Thể tích Hình lập phương


• Tính Thể tích Hình trụ tròn


• Công thức tính thể tích hình lăng trụ


• Tính Thể tích Hình chóp


• Tính Thể tích Hình nón


• Tính Thể tích Hình cầu


• Các bài toán mẫu về phương pháp tính thể tích


• 
  

Tính thể tích hình hộp chữ nhật




Với : a x b x c với a là chiều dài,b là chiều rộng,c là độ cao của hình hộp chữ nhật.









Thể tích hình hộp chữ nhật bằng chiều dài x chiều rộng x độ cao. Nếu chiếc hộp là hình hộp chữ nhật hoặc hình lập phương, bạn chỉ việc đo chiều dài, chiều rộng và độ cao, tiếp theo đó nhân chúng lại là ra thể tích. Công thức này thường được viết tắt là V = l x w x h.



• Ví dụ: “Nếu bạn có một chiếc hộp với chiều dài là 10cm, chiều rộng 4cm, và độ cao 5cm, thể tích của chiếc hộp là bao nhiêu?”


• V= l x w x h


• V= 10cm x 4cm x 5cm


• V= 200cm3


• “Chiều cao” còn được gọi là “chiều sâu”. Ví dụ, “Chiếc hộp có chiều dài 10cm, chiều rộng 4cm, và chiều sâu 5cm”.








Đo chiều dài hộp. Nếu nhìn chiếc hộp từ trên xuống, bạn sẽ thấy mặt trên của chiếc hộp in như một hình chữ nhật phẳng, cạnh dài nhất của hình này là chiều dài chiếc hộp. Bạn đo cạnh này và viết giá trị đó cho “chiều dài”.



• Lưu ý dùng một cty đo cho toàn bộ những cạnh — nếu bạn đo một cạnh bằng cty cm, hãy dùng cty này cho toàn bộ những cạnh còn sót lại.



Đo chiều rộng hộp









Chiều rộng là số đo của cạnh liền kề với cạnh bạn vừa đo chiều dài. Nếu nhìn vào một trong những nửa chiếc hộp, chiều rộng và chiều dài tạo với nhau một chữ “L”. Bạn đo và viết giá trị đó cho “chiều rộng”.



• Chiều rộng luôn luôn là cạnh ngắn lại.



Đo độ cao









Đây là chiều ở đầu cuối bạn chưa đo, và đó là khoảng chừng cách từ mặt trên tới mặt đáy của hộp. Bạn đo và viết giá trị đó cho “độ cao”.



• Tùy thuộc vào cách bạn đặt chiếc hộp, cạnh đo “độ cao” hay “chiều dài” hoàn toàn có thể rất khác nhau. Tuy nhiên, điều này sẽ không còn quan trọng lắm, bạn chỉ việc đo đủ 3 cạnh rất khác nhau là được.



Nhân số đo ba cạnh với nhau









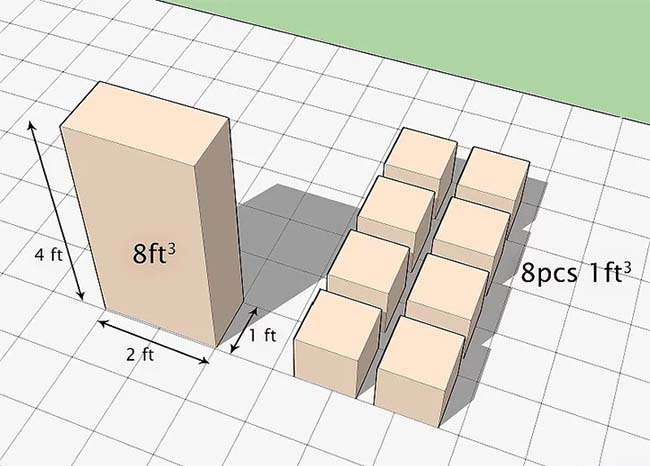
Bạn cần nhớ công thức tính thể tích là V = chiều dài x chiều rộng x độ cao, bạn chỉ việc nhân cả 3 cạnh với nhau là ra thể tích. Bạn nhớ viết cả cty đo để không quên ý nghĩa của số lượng vừa tính.




Thêm “đơn vị3” vào sau thể tích. Thể tích là một số trong những đo, tuy nhiên nếu bạn không biết cty đo thì nó chỉ là một số trong những lượng vô nghĩa. Để viết đúng thể tích, bạn cần thêm vào cty khối. Ví dụ, nếu bạn đo toàn bộ những cạnh bằng cty cm, bạn cần thêm cty “cm3” vào kết quả ở đầu cuối. Ví dụ:



• Bài toán mẫu: “Nếu bạn có một chiếc hộp với chiều dài là 2cm, chiều rộng 1cm, và độ cao 4cm, thể tích của chiếc hộp là bao nhiêu?”


• V = l x w x h


• V = 2cm x 1cm x 4cm


• Thể tích = 8cm3


• Ghi chú: Đơn vị thể tích là khối vì thể tích cho biết thêm thêm bạn hoàn toàn có thể để bao nhiêu khối lập phương vào chiếc hộp của tớ. Chẳng hạn như bạn hoàn toàn có thể để 8 khối lập phương có cạnh 1cm vào chiếc hộp ở ví dụ trên.



Tính thể tích hộp có những hình dạng khác




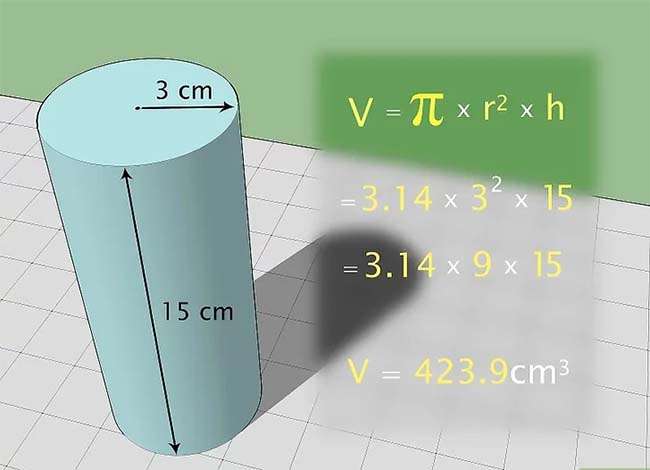Tính thể tích hình trụ




Hình trụ có dạng ống với hai đáy là hình tròn trụ. Để tính thể tích hình trụ, bạn dùng công thức V= pi x r2 x h. Trong số đó pi = 3,14, r là bán kính hình tròn trụ đáy, và h là độ cao.



• Để tính thể tích hình nón, hay hình chóp có đáy tròn, bạn dùng công thức tương tự nhân với cùng 1/3. Ta hoàn toàn có thể tích hình nón =1/3(pi x r2 x h)



Tính thể tích hình chóp









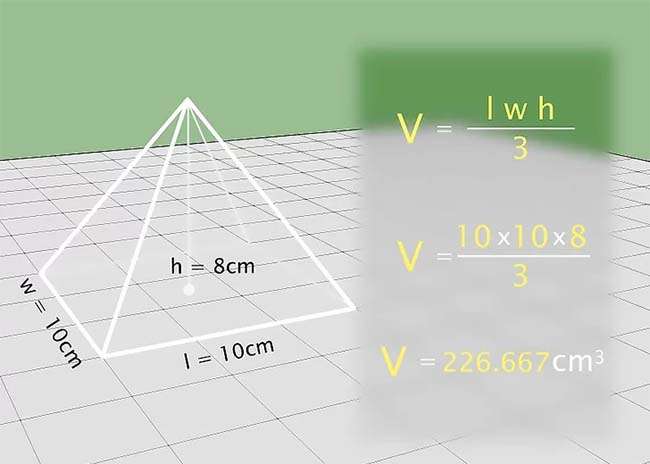
Hình chóp có một cạnh đáy và những cạnh còn sót lại sở hữu chung đỉnh. Để tính thể tích hình chóp, bạn lấy diện tích s quy hoạnh đáy nhân với độ cao, tiếp theo đó nhân với phân số 1/3. Ta hoàn toàn có thể thích hình chóp = 1/3(diện tích s quy hoạnh đáy x độ cao).



• Đa số hình chóp có cạnh đáy là hình vuông vắn hoặc hình chữ nhật. Để tính diện tích s quy hoạnh mặt đáy, bạn chỉ việc lấy chiều dài đáy nhân với chiều rộng.



Cộng thể tích từng phần để tính thể tích của những hình phức tạp









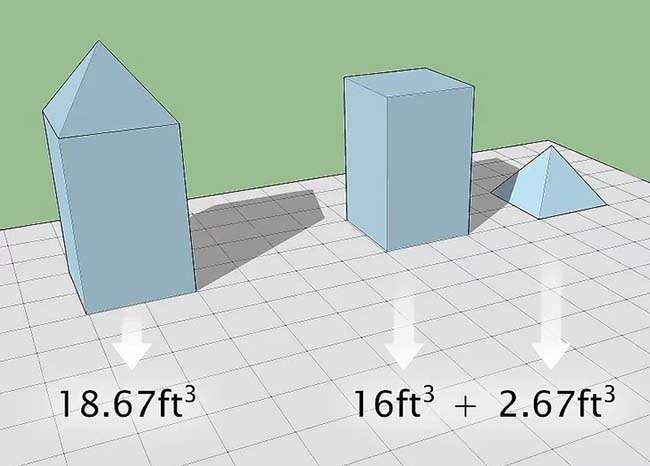
Ví dụ, nếu cần tìm thể tích của một chiếc hộp hình chữ “L”, bạn phải đo nhiều hơn nữa 3 cạnh. Tuy nhiên, nếu coi đó là hai chiếc hộp nhỏ hơn, bạn hoàn toàn có thể tính thể tích của từng hộp nhỏ, tiếp theo đó cộng lại để tìm ra thể tích của chiếc hộp lớn. Lấy ví dụ với chiếc hộp hình chữ “L”, bạn hoàn toàn có thể coi cạnh thẳng đứng là một chiếc hộp hình chữ nhật và cạnh đáy nằm ngang là một chiếc hộp hình vuông vắn.



• Với những trường hợp phức tạp hơn, có thật nhiều phương pháp để bạn tính thể tích của bất kỳ hình dạng nào.



Tính Thể tích Hình lập phương









Nhận biết hình lập phương. Hình lập phương là một hình khối ba chiều có 6 mặt là hình vuông vắn. Nói cách khác, đấy là một hình hộp có toàn bộ những cạnh bằng nhau.



• Một viên xúc xắc 6 mặt là một ví dụ về hình lập phương mà bạn hoàn toàn có thể tìm thấy tận nhà. Viên đường nén hay những khối học chữ của trẻ con cũng thường có hình lập phương.



Công thức tính thể tích hình lập phương









Vì toàn bộ những cạnh của hình lập phương đều bằng nhau nên công thức tính thể tích hình lập phương cũng rất đơn thuần và giản dị. Đó là: V = s3 với V là thể tích, s là cạnh của hình lập phương.



• Để tìm s3, bạn chỉ việc nhân s với chính nó 3 lần, tức là: s3 = s * s * s



Tìm chiều dài của một cạnh hình lập phương









Tùy từng trường hợp mà đề bài hoàn toàn có thể cho sẵn giá trị này, hoặc bạn hoàn toàn có thể phải tự đo cạnh của hình lập phương bằng thước. Vì đấy là hình lập phương, tức là toàn bộ những cạnh đều bằng nhau, nên bạn chỉ việc đo một cạnh bất kỳ.



• Nếu bạn không chắc như đinh 100% rằng hình khối bạn đang đo là hình lập phương, hãy đo toàn bộ những cạnh và xem những giá trị có bằng nhau không. Nếu không bằng nhau, bạn cần vận dụng phương pháp tính thể tích hình hộp chữ nhật sẽ tiến hành nêu ở phần tiếp theo.



Thay chiều dài đo được vào công thức V = s3 và tính









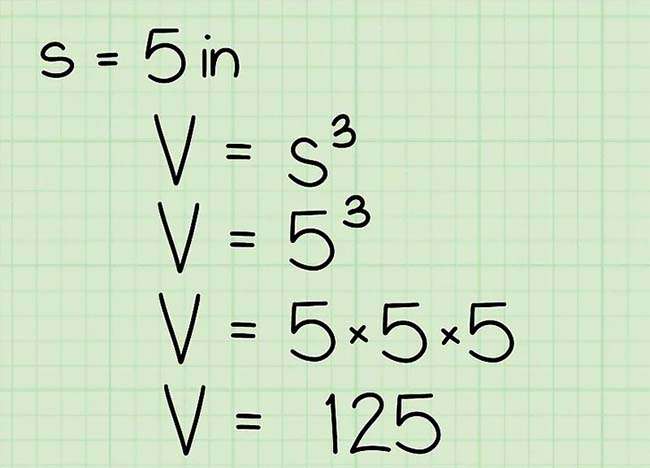
Ví dụ, nếu cạnh của hình lập phương là 5 inches, ta sẽ có được: V = (5 in)3. 5 in * 5 in * 5 in = 125 in3, đây đó đó là thể tích của hình lập phương.




Cần đảm nói rằng bạn viết cty đo theo khối (mũ 3 của cty đo)









Trong ví dụ trên, cạnh của hình lập phương được đo bằng inch, do đó thể tích sẽ có được cty là inch khối. Nếu cạnh của hình lập phương là 3 cm, thể tích của hình lập phương sẽ là V = (3 cm)3, hoặc V = 27 cm3.




Tính Thể tích Hình trụ tròn




Với : πr2h với r là bán kính đáy, h là độ cao.









Nhận biết hình trụ. Hình trụ là một hình khối không khí có hai đáy phẳng là hai hình tròn trụ giống nhau và một mặt cong tiếp nối đuôi nhau hai đáy.



• Một quả pin AA hay pin AAA thường có hình trụ tròn.



Công thức tính thể tích hình trụ tròn




Để tính thể tích hình trụ tròn, bạn nên phải ghi nhận độ cao của hình đó và đường kính mặt đáy (hay khoảng chừng cách từ tâm tới cạnh của hình tròn trụ). Công thức để tính thể tích hình trụ tròn như sau: V = πr2h với V là Thể tích, r là bán kính của mặt đáy, h là độ cao của hình trụ, và π là hằng số pi.



• Trong một số trong những vướng mắc hình học, câu vấn đáp hoàn toàn có thể được đưa dưới dạng tỉ số của pi, nhưng trong phần lớn những trường hợp, ta hoàn toàn có thể làm tròn và lấy giá trị của pi là 3,14. Hãy hỏi giáo viên của bạn xem bạn nên dùng dạng nào.


• Công thức để tính thể tích hình trụ tròn rất giống với công thức tính thể tích hình hộp chữ nhật: nhân độ cao (h) với diện tích s quy hoạnh đáy. Đối với hình hộp chữ nhật, diện tích s quy hoạnh đáy là l * w, riêng với hình trụ tròn, diện tích s quy hoạnh mặt đáy hình tròn trụ bán kính r là πr2.



Tìm bán kính của mặt đáy




Nếu giá trị này được ghi trong giản đồ, bạn hoàn toàn có thể sử dụng luôn. Nếu đề bài cho đường kính (thường kí hiệu là d) của mặt đáy, bạn chỉ việc chia giá trị này cho 2 là sẽ tiến hành bán kính (vì d = 2r).









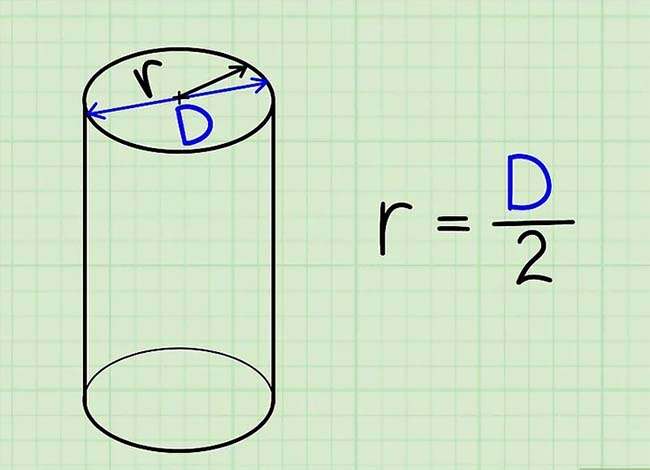
Tiến hành đo hình trụ để tìm bán kính mặt đáy









Cần để ý quan tâm rằng để đã có được một thông số đúng chuẩn nào đó của một hình tròn trụ yên cầu sự khôn khéo của bạn. Cách thứ nhất bạn hoàn toàn có thể sử dụng đó là tìm và đo phần rộng nhất của mặt đáy của hình trụ tròn và chia giá trị đó cho 2 để được bán kính.



• Một cách khác để tính bán kính là đo chu vi của mặt đáy (độ dài đường viền của hình tròn trụ) với thước dây hoặc một đoạn dây mà bạn hoàn toàn có thể ghi lại, tiếp theo đó đo lại với thước kẻ. Khi đã có được chu vi, bạn vận dụng công thức sau: C (Chu vi) = 2πr. Chia chu vi cho 2π (hay 6,28) và bạn sẽ tìm kiếm giá tốt trị của bán kính.


• Ví dụ, nếu chu vi bạn đo được là 8 inches, bán kính sẽ là một trong,27 in.


• Nếu bạn muốn tìm kiếm giá tốt trị thực sự đúng chuẩn của chu vi, bạn hoàn toàn có thể vận dụng và so sánh kết quả đã có được từ hai phương pháp trên, nếu kết quả có sự sai lệch đáng kể, hãy kiểm tra lại. Phương pháp tính theo chu vi thường sẽ cho kết quả đúng chuẩn hơn.



Tính diện tích s quy hoạnh mặt đáy của hình trụ tròn









Thế giá trị của bán kính vào công thức πr2. Sau đó nhân bán kính với chính nó một lần nữa, lấy kết quả thu được nhân với π. Ví dụ:



• Nếu bán kính của hình tròn trụ là 4 inches (tương tự 10,16 cm), diện tích s quy hoạnh của mặt đáy sẽ là A = π42.


• 42 = 4 * 4, hay 16. 16 * π (3.14) = 50.24 in2


• Nếu biết đường kính của mặt đáy, hãy nhớ công thức: d = 2r. Bạn chỉ việc lấy giá trị của đường kính chia cho 2 là giá tốt trị của bán kính.



Tìm độ cao của hình trụ tròn









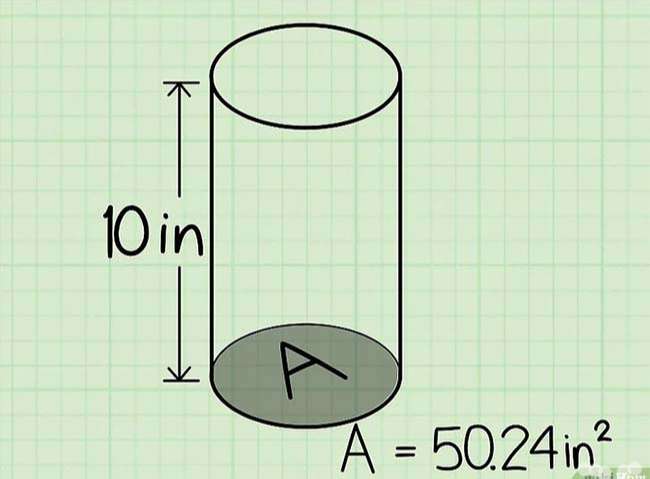
Chiều cao của hình trụ tròn đó đó là khoảng chừng cách giữa hai mặt đáy. Hãy tìm kí hiệu độ cao (thường là h) trên giản đồ hoặc dùng thước để đo trực tiếp.




Nhân diện tích s quy hoạnh mặt đáy với độ cao để được thể tích









Hoặc bạn hoàn toàn có thể làm tắt bằng phương pháp thay giá trị bán kính mặt đáy và độ cao hình trụ tròn vào công thức V = πr2h. Với ví dụ nêu trên, bán kính mặt đáy là 4 inches và độ cao là 10 inches:



• V = π4210


• π42 = 50,24


• 50,24 * 10 = 502,4


• V = 502,4




Kết quả tính toán cần phải biểu thị theo khối (mũ 3 của cty đo)









Hình trụ tròn trong ví dụ trên được đo theo cty inches, vậy thể tích của hình trụ tròn này còn có cty là inch mũ 3: V = 502.4in3. Nếu hình trụ tròn của bạn được đo theo cty centimet, thể tích của hình đó cần phải ghi theo cty là centimet khối (cm3).




Công thức tính thể tích hình lăng trụ




Trong hình học, hình lăng trụ là một đa diện có hai mặt đáy là những đa giác tương đẳng và những mặt còn sót lại là những hình bình hành.Mọi tiết diện tuy nhiên tuy nhiên với hai đáy đều là những đa giác tương đẳng với hai đáy.









Tính Thể tích Hình chóp




Nhận diện hình chóp









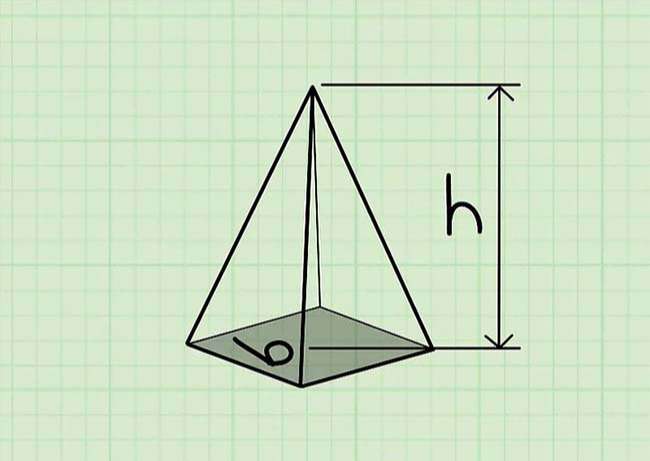
Một hình chóp là một hình khối không khí có đáy là một đa giác và những mặt bên của hình chóp giao nhau tại một điểm gọi là đỉnh của hình chóp. Một hình chóp đa giác đều là một hình chóp có đáy là một đa giác đều, tức là toàn bộ những cạnh của đa giác bằng nhau và toàn bộ những những góc của đa giác cũng bằng nhau.



• Chúng ta thường tưởng tượng ra hình chóp với đáy là hình vuông vắn và những mặt của hình chóp giao nhau tại một điểm, nhưng mặt đáy của một hình chóp hoàn toàn có thể có 5, 6 hoặc thậm chí còn 100 cạnh!


• Một hình chóp có đáy là hình tròn trụ thì được gọi là hình nón, toàn bộ chúng ta sẽ nói về thể tích hình nón ở phần sau.



Công thức tính thể tích hình chóp đa giác đều









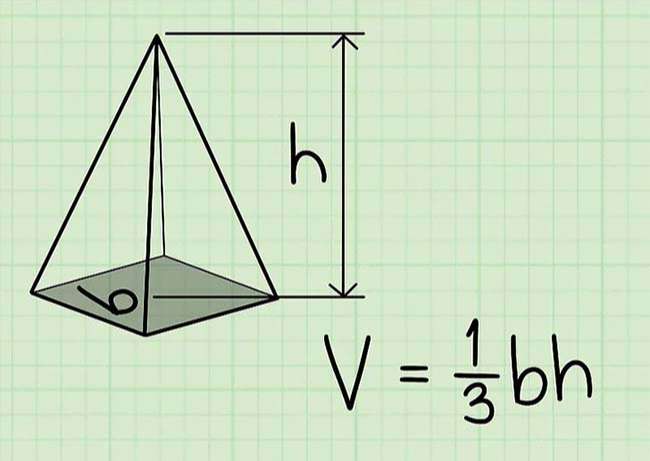
Công thức tính thể tích hình chóp đa giác đều là V=1/3bh, với b là thể tích mặt đáy (đa giác đáy) và h là độ cao của hình chóp, cũng đó đó là khoảng chừng cách từ đỉnh của hình chóp tới mặt đáy của nó).



• Công thức tính thể tích hình chóp đều cũng tương tự như trên, trong số đó hình chiếu của đỉnh đa giác xuống mặt đáy đó đó là tâm của mặt đáy, và với hình chóp xiên thì hình chiếu của đỉnh xuống mặt đáy không phải là tâm của đáy.



Tính diện tích s quy hoạnh mặt đáy









Công thức tính diện tích s quy hoạnh mặt đáy tùy từng số cạnh của đa giác tạo thành mặt đáy. Đối với hình chóp trong giản đồ mà ta có ở đây, mặt đáy là hình vuông vắn với những cạnh có kích thước là 6 inches. Ta có công thức tính diện tích s quy hoạnh hình vuông vắn là A = s2, với s là chiều dài cạnh hình vuông vắn. Vậy với hình chóp này, diện tích s quy hoạnh của mặt đáy là (6 in) 2, hay 36 in2.



• Công thức tính thể tích hình chóp có đáy là hình tam giác là: A = 1/2bh, với b là diện tích s quy hoạnh đáy và h là độ cao.


• Ta hoàn toàn có thể tính được diện tích s quy hoạnh của bất kể đa giác nào bằng phương pháp vận dụng công thức A = 1/2pa, với A là diện tích s quy hoạnh, p. là chu vi và a là trung đoạn, trung đoạn đó đó là khoảng chừng cách từ tâm của của đa giác tới trung điểm của một cạnh bất kỳ. Công thức này nằm ngoài mục tiêu của bài này, nhưng bạn hoàn toàn có thể click more phương pháp tính diện tích s quy hoạnh của một đa giác để biết rõ hơn về kiểu cách vận dụng công thức trên.



Tìm độ cao của hình chóp









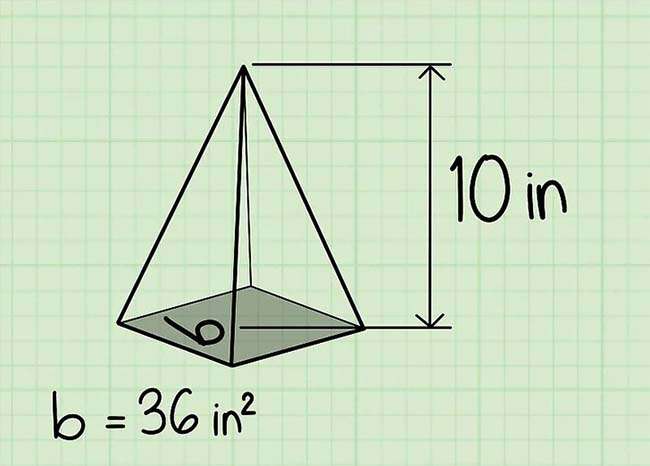
Trong hầu hết những trường hợp, giá trị này sẽ tiến hành cho theo giản đồ. Với ví dụ mà toàn bộ chúng ta đang xét, độ cao của hình chóp là 10 inches.




Nhân diện tích s quy hoạnh của mặt đáy với độ cao, tiếp theo đó chia kết quả thu được cho 3









Ta có công thức tính thể tích hình chóp là V=1/3bh. Với hình chóp mà ta đang lấy làm ví dụ, diện tích s quy hoạnh đáy là 36 và độ cao là 10, vậy thể tích là: 36 * 10 * 1/3, hay 120.



• Nếu ta có một hình chóp khác với mặt đáy là hình ngũ giác có diện tích s quy hoạnh là 26, độ cao là 8, thể tích của hình chóp này sẽ là một trong/3 * 26 * 8 = 69.33.



Cần nhớ biểu thị kết quả tính được theo khối (mũ 3 của cty đo)









Hình chóp mà toàn bộ chúng ta đang xét có kích thước được đo bằng inch, vì thế thể thích của hình chóp sẽ có được cty là inch khối, 120 in3. Nếu hình chóp có những kích thước được biểu thị theo cty là mét, thể tích hình chóp sẽ có được cty là m3.




Tính Thể tích Hình nón




Với: πr2h/3 với r là bán kính đáy, h là độ cao.









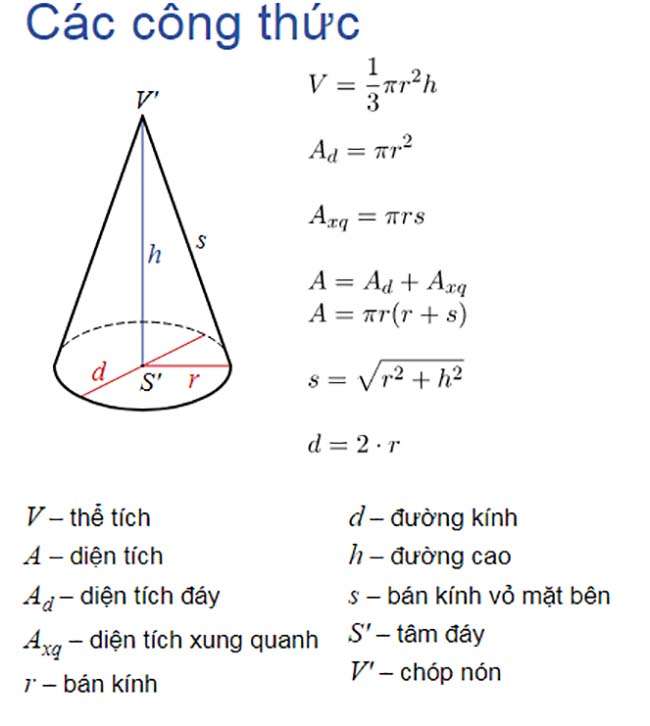
Các điểm lưu ý của hình nón









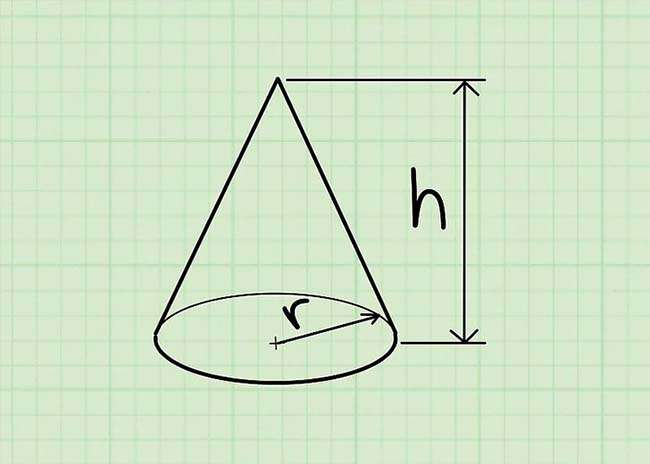
Hình nón là một hình khối không khí ba chiều xuất hiện đáy là hình tròn trụ và một đỉnh duy nhất. Bạn hoàn toàn có thể tưởng tượng hình nón là một hình chóp có đáy là hình tròn trụ.



• Nếu hình chiếu của đỉnh xuống mặt đáy của hình nón trùng với tâm của mặt đáy, ta gọi đó là “hình nón đều”. trái lại ta gọi đó là “hình nón xiên”. Tuy nhiên công thức tính thể tích của toàn bộ hai dạng hình nón này là giống nhau.




Công thức tính thể tích hình nón









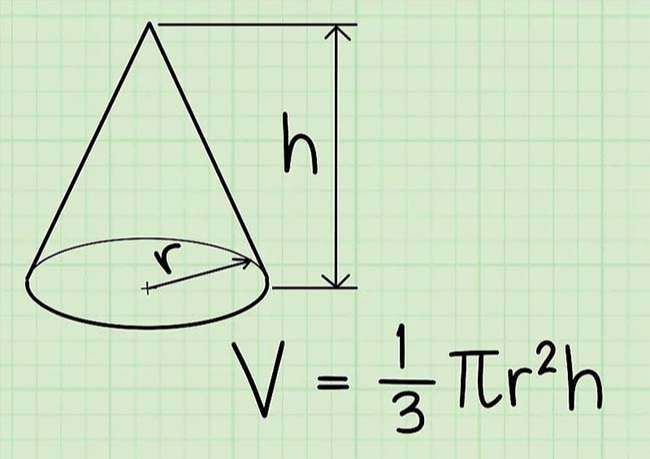
V = 1/3πr2h là công thức tính thể tích một hình nón bất kỳ, trong số đó r là bán kính mặt đáy, h là độ cao của hình nón và π là hằng số pi, ta hoàn toàn có thể làm tròn và lấy giá trị của π là 3,14.



• Trong công thức trên, πr2 đó đó là diện tích s quy hoạnh của mặt đáy. Từ đó ta hoàn toàn có thể thấy rằng công thức tính thể tích hình nón đó đó là một trong/3bh, cũng đó đó là công thức tính thể tích hình chóp mà ta đã xét ở trên.



Tính diện tích s quy hoạnh mặt đáy của hình nón









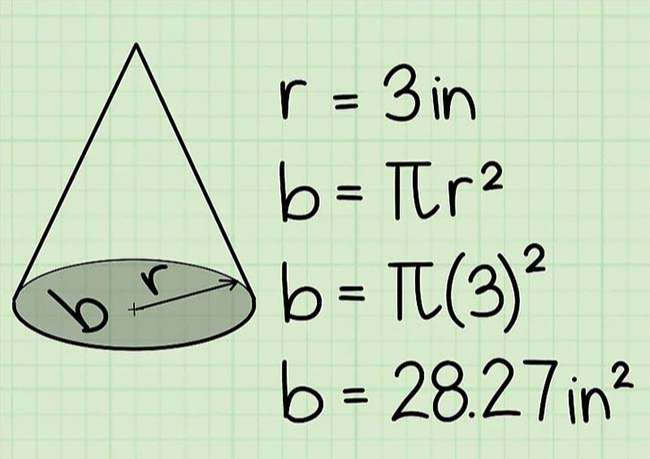
Để tính giá tốt trị này, ta nên phải ghi nhận bán kính của mặt đáy, giá trị này hoàn toàn có thể được đưa ra trong giản đồ. Nếu đề bài cho đường kính thay vì bán kính, bạn chỉ việc chia đường kính cho 2 vì đường kính có mức giá trị gấp 2 lần bán kính. Sau đó thay giá trị bán kính tìm kiếm được vào công thức tính diện tích s quy hoạnh hình tròn trụ A = πr2.



• Với ví dụ đưa ra trong giản đồ, bán kính mặt đáy của hình nón là 3 inches. Thay giá trị này vào công thức, ta có: A = π32.


• 32 = 3 *3, hay 9, vậy A = 9π.


• A = 28.27 in2



Tìm độ cao của hình nón









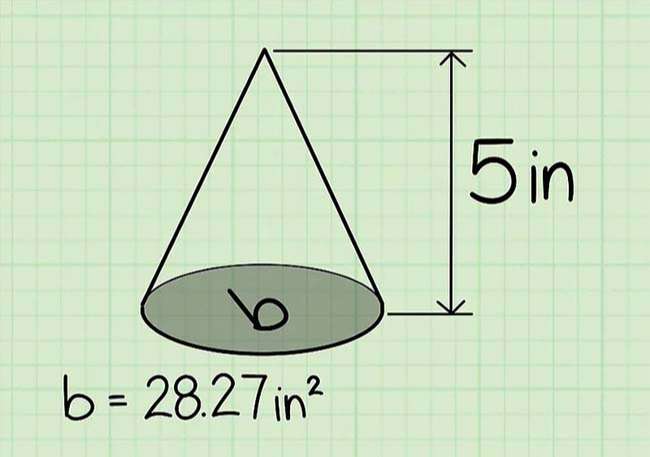
Chiều cao của hình nón là khoảng chừng cách giữa đỉnh của hình nón và mặt đáy của nó. Trong ví dụ ta đang xét, độ cao của hình nón là 5 inches.




Nhân diện tích s quy hoạnh mặt đáy với độ cao của hình nón









Ở ví dụ này, diện tích s quy hoạnh của hình nón là 28,27 in2 và độ cao là 5 in, vậy bh = 28,27 * 5 = 141,35.




Để tính thể tích hình nón, ta lấy giá trị thu được ở phép tính trên nhân với cùng 1/3 (hoặc chia cho 3)









Ở bước trên, toàn bộ chúng ta đã tính thể tích của hình trụ hoàn toàn có thể tạo thành nếu mặt bên của hình nón được mở rộng và tạo thành một mặt đáy khác thay vì chụm lại tại một điểm. Chia giá trị thu được ở bước trên cho 3 ta sẽ đã có được thể tính của hình nón mà ta đang xét.



• Vậy, trong ví dụ này, thể tích của hình nón là 141,35 * 1/3 = 47,12.


• Ta hoàn toàn có thể rút gọn tiến trình tính lại và được một/3π325 = 47,12








Trong ví dụ ở trên, những giá trị được xem theo inch, vậy nên thể tích cần phải ghi là 47.12 in3.




Tính Thể tích Hình cầu









Hình cầu là một vật thể không khí tròn hoàn toàn với mức chừng cách từ một điểm bất kỳ trên mặt cầu tới tâm của hình cầu là một số trong những không đổi. Nói cách khác, hình cầu là hình quả bóng.




Công thức tính thể tích hình cầu









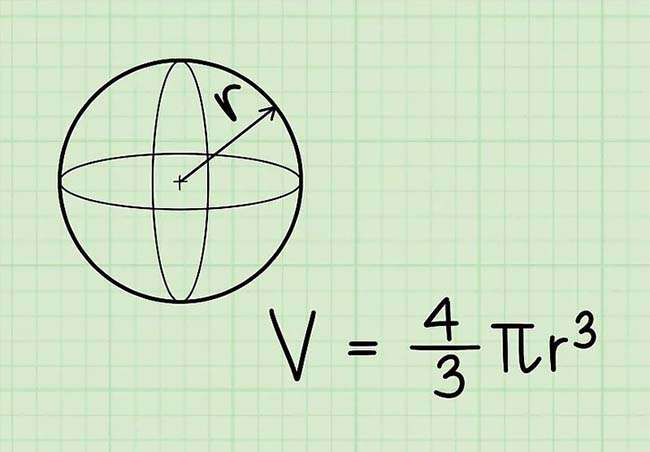
Công thức tính thể tích hình cầu là V = 4/3πr3 (bằng chữ: “bốn lần pi chia 3 nhân với r mũ 3”) với r là bán kính của hình cầu, π là hằng số pi (3.14)




Tìm bán kính của hình cầu









Nếu bán kính được cho trước trong giản đồ, việc tìm bán kính chỉ là xem nó được ghi lại ở đâu. Nếu đề bài cho đường kính, ta tìm bán kính bằng phương pháp chia đôi đường kính. Ví dụ, bán kính của hình cầu trong giản đồ cho ở đấy là 3 inches.




Đo bán kính nếu chưa chắc như đinh giá trị này









Nếu bạn nên phải đo một hình cầu (như bóng tennis ví dụ điển hình) để tìm bán kính, thứ nhất hãy tìm một đoạn dây đủ dài để cuốn quanh hình cầu đó. Sau đó dùng đoạn dây này cuốn quanh hình cầu tại phần rộng nhất và ghi lại giao điểm của đoạn dây. Dùng thước kẻ để đo đoạn dây ta sẽ đã có được chu vi. Chia giá trị này cho 2π, hoặc 6,28, để được bán kính của hình cầu.



• Ví dụ, nếu bạn đo một quả bóng và đã có được chu vi của quả bóng là 18 inches, lấy số đó chia cho 6,28 và ta tìm kiếm giá tốt trị của bán kính là 2,87 in.


• Đo một hình cầu hoàn toàn có thể cần sự khôn khéo của bạn, vì vậy để đã có được kết quả đúng chuẩn nhất hoàn toàn có thể, bạn nên đo lặp lại 3 lần tiếp theo đó lấy giá trị trung bình (cộng giá trị thu được sau 3 lần đo lại và tiếp theo đó chia cho 3).


• Ví dụ, nếu chu vi bạn đo được sau 3 lần đo là 18 inches, 17,75 inches, và 18,2 inches, bạn hãy cộng những giá trị nó lại (18 + 17,5 + 18,2 = 53,95) và chia tổng tìm kiếm được cho 3 (53,95/3 = 17,98). Hãy dùng giá trị này để tính toán thể tích.



Mũ 3 bán kính đã có để được r3









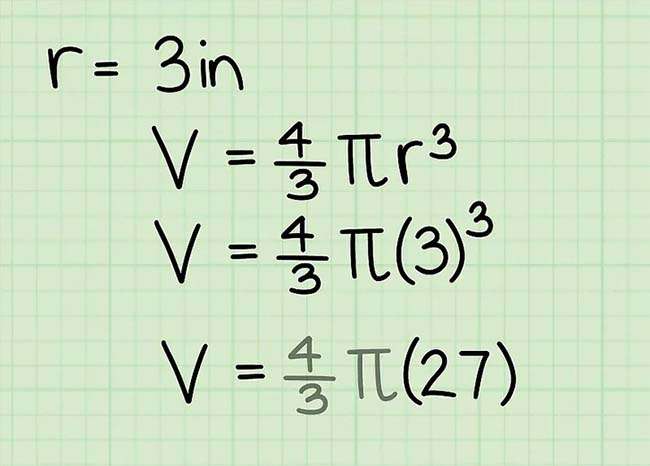
Mũ 3 bán kính đó đó là nhân bán kính với chính nó 3 lần, vậy r3 = r * r * r. Trong ví dụ mà ta đang xét, r = 3, vậy r3 = 3 * 3 * 3, hay bằng 27.




Nhân kết quả tìm kiếm được với 4 / 3









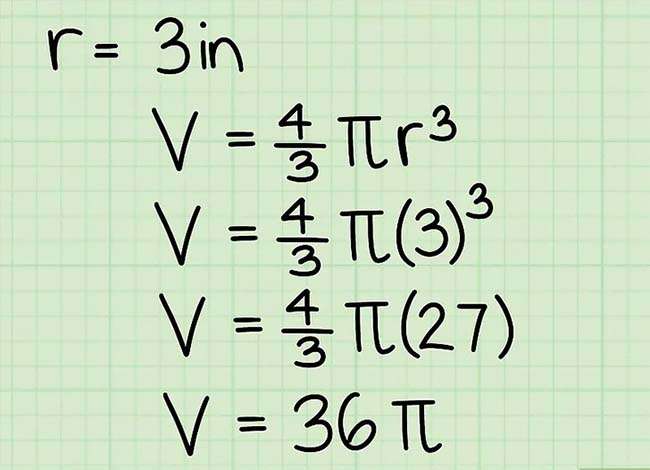
Bạn hoàn toàn có thể sử dụng máy tính, hoặc nhân bằng tay thủ công tiếp theo đó rút gọn phân số tìm kiếm được. Trong ví dụ mà ta đang xét, nhân 27 với 4/3 ta được 108/3, rút gọn phân số này ta được 36.




Lấy kết quả phép nhân ở bước trên nhân tiếp với π để tính thể tích hình cầu









Bước ở đầu cuối trong quy trình tính thể tích hình cầu là nhân kết quả thu được ở bước trên với π. Làm tròn giá trị của π tới 2 số sau dấu phẩy, giá trị này thường được đồng ý trong hầu hết những đề toán (trừ khi giáo viên của bạn yêu cầu khác), vậy nhân với 3,14 và bạn sẽ tiến hành thể tích hình cầu.



• Trong ví dụ đang xét, 36 * 3,14 = 113,04.



Ghi kết quả thu được theo cty khối









Vì trong ví dụ đang xét ta có bán kính của hình cầu được xem theo inch, vì vậy kết quả của toàn bộ chúng ta là V = 113.04 inch khối (113.04 in3).




Các bài toán mẫu về phương pháp tính thể tích




Công thức tính nhanh thể tích của khối tứ diện cho một số trong những trường hợp đặc biệt quan trọng hay gặp









Chứng minh









Share Link Cập nhật Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này còn có diện tích s quy hoạnh là miễn phí




Bạn vừa đọc tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Video Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này còn có diện tích s quy hoạnh là tiên tiến và phát triển nhất và ShareLink Download Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này còn có diện tích s quy hoạnh là Free.





Thảo Luận vướng mắc về Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này còn có diện tích s quy hoạnh là




Nếu sau khi đọc nội dung bài viết Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này còn có diện tích s quy hoạnh là vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Tác giả lý giải và hướng dẫn lại nha

#Tính #thể #tích #của #một #hình #hộp #chữ #nhật #biết #rằng #mặt #của #hình #này #có #diện #tích #là

Related posts: