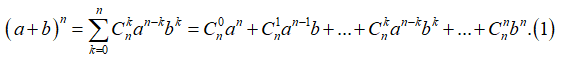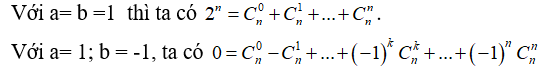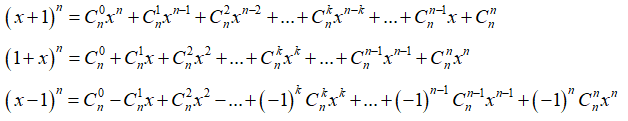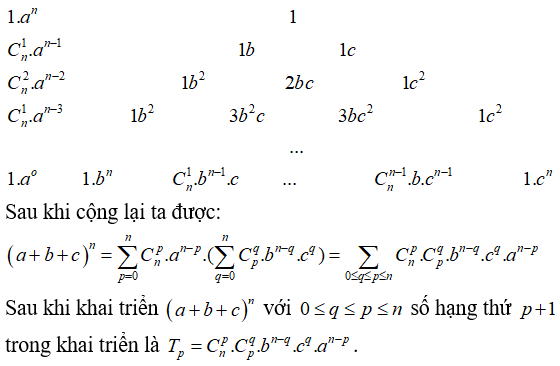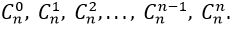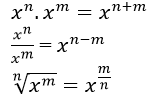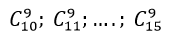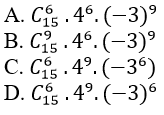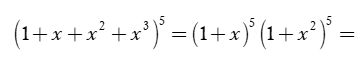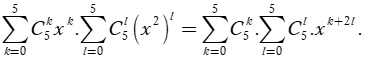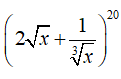Kinh Nghiệm về Viết khai triển theo công thức nhị thức Niu-tơn (x y 4) Chi Tiết
Bạn đang tìm kiếm từ khóa Viết khai triển theo công thức nhị thức Niu-tơn (x y 4) được Cập Nhật vào lúc : 2022-04-28 08:38:12 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Áp dụng Công thức khai triển nhị thức Newton: (left( x + y right)^n = sumlimits_i = 0^n C_n^ix^i.y^n – i ).
-
Tải app VietJack. Xem lời giải nhanh hơn!
Quảng cáo
1. Công thức nhị thức Niu-tơn
Với a, b là những số thực và n là sô nguyên dương, ta có :
Công thức trên được gọi là công thức nhị thức Newton (viết tắt là Nhị thức Newton).
Quy ước: a0 = b0 = 1
Chú ý :
Trong biểu thức ở vế phải của công thức (1)
+ Số những hạng tử là n + 1.
+ Các hạng tử có số mũ của a giảm dần từ n đến 0, số mũ của b tăng dần từ 0 đến n, nhưng tổng những số mũ của a và b trong mọi hạng tử luôn bằng n.
+ Các thông số của mỗi hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.
Hệ quả :
Các dạng khai triển cơ bản nhị thức Newton
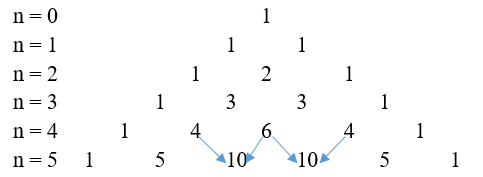
2. Tam giác Pascal.
Tam giác Pascal được thiết lập theo quy luật sau :
– Đỉnh được ghi số 1. Tiếp theo là hàng thứ nhất ghi hai số 1.
– ¬Nếu biết hàng thứ n ( n≥1) thì hàng thứ n+1tiếp theo được thiết lập bằng phương pháp cộng hai số liên tục của hàng thứ n rồi viết kết quả xuống hàng dưới ở vị trí giữa hai số này. Sau đó viết số 1 ở đầu và cuối hàng.
Nhận xét :
3. Mở rộng của khai triển nhị thức Niu- tơn
Bước 1:Viết tam giác Pascal đến dòng thứ nđể đã có được thông số của nhị thức Niuton (b+ c)n
Bước 2: Ở những đầu dòng ta viết những đơn thức là khai triển nhị thức Newton
Bước 3: Nhân lần lượt những đơn thức ở đầu dòng mỗi cột với những đơn thức còn sót lại trên mỗi dòng đó rồi cộng những kết quả lại, ta thu được kết quả khai triển.
Quảng cáo
Cụ thể ta có ở dưới đây
Chú ý 1:
Chú ý 2:
Ví dụ 1: Tính thông số x10y8 trong khai triển ( x + y)18?
A.43758 B.23145 C.45 D.12458
Hướng dẫn giải :
Đáp án : A
Theo công thức nhị thức Niu- tơn; thông số chứa x10.y8 là:
Ví dụ 2: Tìm thông số của x4 trong khai triển ( 2x- 5)7
A.175000 B.–70000 C.70000 D.-175000
Hướng dẫn giải :
Đáp án : B
Ta có: (2x – 5)7 = [ (2x + (-5)]7
Theo công thức nhị thức Niu-tơn; số hạng chứa x4 là:
Do đó thông số của x4 là:
Quảng cáo
Ví dụ 3: Trong khai triển nhị thức (x + 1)n+9. Có toàn bộ 17 số hạng. Vậy n bằng:
A.10 B.17 C.9 D.12
Hướng dẫn giải :
Đáp án : C
Chú ý: Số những số hạng của khai triển mũ n là n + 1.
Vậy khai triển (x+1)n+ 9 có toàn bộ 17 số hạng suy ra n + 9= 17 + 1.
⇔ n + 9= 18 nên n= 9
Ví dụ 4: Tìm thông số chứa x9 trong khai triển
(1+x)9+(1+x)10+(1+x)11+(1+x)12+(1+x)13+(1+x)14+(1+x)15
Hướng dẫn giải :
Đáp án : B
+ Trong khai triển (1+x)9 thì số hạng chứa x9 là:
+ Tương tự thông số chứa x9 trong những khai triển ( 1+x)10; ( 1+ x)11; ( 1+ x)12; …; ( 1+ x)15 là
Do đó; thông số chứa x9 cần tìm là:
.
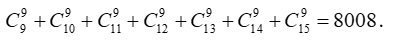
Ví dụ 5: Trong khai triển
, hai số hạng cuối là:
.
Hướng dẫn giải :
Đáp án : A
Ta có:
là hai số hạng ở đầu cuối của khai triển
Ví dụ 6: Trong khai triển (2∛x+3√x )10,(x>0) số hạng chứa x4 sau khi khai triển là
A.1808640 B.1088640×4 C.1808460×4 D.207360
Hướng dẫn giải :
Đáp án : B
Ví dụ 7: Hệ số của số hạng chứa x9 trong khai triển (4/3-3×3)15 là
Hướng dẫn giải :
Đáp án : D
Ví dụ 8: Trong khai triển (1+ 3x)20 với số mũ tăng dần, thông số của số hạng đứng ở chính giữa là:
Hướng dẫn giải :
Đáp án : D
Ví dụ 9: Nếu bốn số hạng đầu của một hàng trong tam giác Pascal được ghi lại là:
1 16 120 560
A. 1 32 360 1680
B. 1 18 123 564
C. 1 17 137 697
D. 1 17 136 680
Khi đó 4 số hạng đầu của hàng tiếp theo đó là:
Hướng dẫn giải :
Đáp án : D
4 số hạng tiếp theo của tam giác Pascal là:
1 1+16=17 16+120=126 120+560=680
Ví dụ 10: Tổng của số hạng thứ 4 trong khai triển (5a-1)5 và số hạng thứ 5 trong khai triển (2a- 3)6 là:
A.4160a2 B.-4160a2 C.4610a2 D.4620a2
Hướng dẫn giải :
Đáp án : C
Ví dụ 11: Hệ số của số hạng chứa x4 trong khai triển P(x)=(3×2 + x + 1)10 là :
A.1695 B.1485 C.405 D.360
Hướng dẫn giải :
Đáp án : A
Ví dụ 12: Tìm số hạng chứa x13 trong khai triển thành những đa thức của (x + x2 + x3 )10 là :
A.180 B.210 C.210×13 D. 180×3
Hướng dẫn giải :
Đáp án : C
+ Với 0≤q≤p.≤10 thì số hạng tổng quát của khai triển (x+x2+x3)10 là:
Ví dụ 13: Tìm thông số chứa x10 trong khai triển (1+ x+ x2 + x3)5
A.98 B.84 C.101 D.121
Hướng dẫn giải :
Đáp án : C
Theo khai triển nhị thức Niu-tơn, ta có:
Câu 1: Số hạng không chứa x trong khai triển là
Hiển thị đáp án
Đáp án : B
Ta có số hạng thứ k+ 1 là :
Số hạng không chứa x tương ứng với: (60-5k)/6=0
⇔ 60 – 5k= 0 ⇔ k= 12.
Do vậy số hạng cần tìm là:
Câu 2: Trong khai triển ( x – y)11, thông số của số hạng chứa x8y3 là:
Hiển thị đáp án
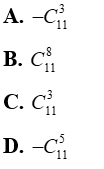
Đáp án : A
Câu 3: Trong khai triển nhị thức (2+ x)6 xét những xác lập sau:
I. Gồm có 7 số hạng.
II. Số hạng thứ 3 là 16x.
III. Hệ số của x5 là 12.
Trong những xác lập trên
A. Chỉ I và III đúng
B. Chỉ II và III đúng
C. Chỉ I và II đúng
D. Cả ba đúng
Hiển thị đáp án
Đáp án : A
Câu 4: Có bao nhiêu số hạng hữu tỉ trong khai triển
.
A.37 B.38 C.36 D.39
Hiển thị đáp án
Đáp án : B
⇒ k= 8t ( với t nguyên)
Lại có: 0≤k≤300 nên 0≤8t≤300
⇔ 0≤t≤37,5. Mà t nguyên nên t ∈ 0,1,2,3…, 37.
Có 38 giá trị nguyên của t thỏa mãn nhu cầu. Suy ra có 38 giá trị của k thỏa mãn nhu cầu.
⇒ Có 38 số hạng hữu tỉ trong khai triển đã cho.
Câu 5: Tìm thông số của x5 trong khai triển P(x) = ( x+1)6 +(x+ 1)7 + ( x+ 1)8 + ..+ (x+ 1)12 .
A.1711 B.1287 C.1716 D.1715
Hiển thị đáp án
Đáp án : D
Câu 6: Tìm thông số chứa x12 trong khai triển ( 3x+ x2)10
A.145654 B.298645 C.295245 D.Đáp án khác
Hiển thị đáp án
Đáp án :
Theo khai triển nhị thức Niu-tơn, ta có số hạng thứ k+ 1 trong khai triển là:
Câu 7: Khai triển đa thức P(x) = (5x – 1)2003 ta được :
P(x)= a2003.x2003 + a2002.x2002 + …+ a1x+ a0.
Mệnh đề nào sau này đúng?
Hiển thị đáp án
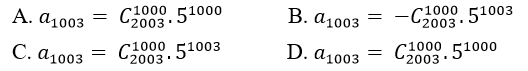
Đáp án : C
Câu 8: Tìm thông số chứa x4 trong khai triển (2x+ 1/2x)10
A.1960 B.1920 C.1864 D.1680
Hiển thị đáp án
Đáp án : B
Câu 9: Tìm số hạng không chứa x trong khai triển: ( xy2- 1/xy)8
A.70y4 B.25y4 C.50y5 D.80y4
Hiển thị đáp án
Đáp án :
Theo khai triển nhị thức Niu-tơn, ta có:
Số hạng không chứa x ứng với: 8 – 2k=0 ⇔ k= 4
⇒ số hạng cần tìm
Câu 10: Tìm số hạng đứng vị trí ở chính giữa trong khai triển: ( x2+ xy)20
Hiển thị đáp án
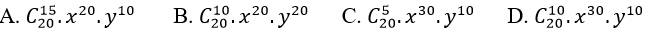
Đáp án : D
Theo khai triển nhị thức Niu-tơn, ta có:
Câu 11: Khai triển đa thức: P(x)= ( 2 x- 1)1000 ta được:
P(x)= a1000x1000 + a999x999+ ….+ a1x+ a0 .Tính a1000 + a999 + …+ a1 + a0 ?
A.-1 B.0 C.2 D.1
Hiển thị đáp án
Đáp án : D
Ta có: (x) = a1000x1000 + a999x999+ ….+ a1x+ a0
Cho x = 1 ta được P(1) = a1000 + a999 + a998 + …+ a1+ a0 (1)
Mặt khác: P(x) = ( 2x-1)1000 nên P(1)= (2.1 – 1)1000 = 1 (2)
Từ (1) và (2) suy ra: a1000 + a999 + a998 + …+ a1+ a0 = 1
Câu 12: Tìm thông số của x5 trong khai triển P(x) = x.(2+ x)5 + x2( 1 + x )10
A.110 B.120 C.130 D.140
Hiển thị đáp án
Đáp án : C
Câu 13: Số hạng không chứa x trong khai triển (x2 + 1/x – 1)10 là
A.1951 B.1950 C.3150 D.-360
Hiển thị đáp án
Đáp án : A
Câu 14: Số hạng chứa x8 trong khai triển (x3 – x2 -1)8 là
A.168×8 B.168 C.238×8 D.238
Hiển thị đáp án
Đáp án : D
Câu 15: Tìm thông số của x5 trong khai triển P(x)= (1+ x)+ 2(1+x)2 + …+ 8(1+x)8
A.487 B.636 C.742 D.568
Hiển thị đáp án
Đáp án : B
Các biểu thức ( 1 + x ) ; 2( 1 + x )2 ; 3(1+x)3 ; 4(1+ x)4 không chứa số hạng chứa x5
Hệ số của số hạng chứa x5 trong khai triển 5(1+x)5 là
Hệ số của số hạng chứa x5 trong khai triển 6(1+x)6 là
Hệ số của số hạng chứa x5 trong khai triển 7(1+x)7 là
Hệ số của số hạng chứa x5 trong khai triển 8(1+ x)8 là
Vậy thông số của x5 trong khai triển P(x) là :
Xem thêm những dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:
Giới thiệu kênh Youtube VietJack
-
Hỏi bài tập trên ứng dụng, thầy cô VietJack vấn đáp miễn phí!
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi trực tuyến, Bài giảng….miễn phí. Tải ngay ứng dụng trên Android và iOS.
Nhóm học tập facebook miễn phí cho teen 2k5: fb.com/groups/hoctap2k5/
Theo dõi chúng tôi miễn phí trên social facebook và youtube:
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các phản hồi không phù phù thích hợp với nội quy phản hồi website sẽ bị cấm phản hồi vĩnh viễn.
to-hop-xac-suat.jsp
Reply
0
0
Chia sẻ
Chia Sẻ Link Download Viết khai triển theo công thức nhị thức Niu-tơn (x y 4) miễn phí
Bạn vừa Read tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Review Viết khai triển theo công thức nhị thức Niu-tơn (x y 4) tiên tiến và phát triển nhất và Chia SẻLink Tải Viết khai triển theo công thức nhị thức Niu-tơn (x y 4) miễn phí.
Hỏi đáp vướng mắc về Viết khai triển theo công thức nhị thức Niu-tơn (x y 4)
Nếu sau khi đọc nội dung bài viết Viết khai triển theo công thức nhị thức Niu-tơn (x y 4) vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha
#Viết #khai #triển #theo #công #thức #nhị #thức #Niutơn