Thủ Thuật về Ý nghĩa của hình thoi Chi Tiết
Pro đang tìm kiếm từ khóa Ý nghĩa của hình thoi được Update vào lúc : 2022-04-05 08:30:06 . Với phương châm chia sẻ Bí quyết Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Hình thoi là gì? Công thức tính diện tích s quy hoạnh, chu vi, đường chéo và những ví dụ thực tiễn sẽ tiến hành giải đáp trong nội dung bài viết này. Các bạn tìm hiểu thêm nội dung bài viết nhé.
Nội dung chính
- 1. Hình thoi là gì?
- 1.1. Đặc điểm
- 1.2. Một hình thoi hoàn toàn có thể có ba tên tương hỗ update
- 1.3. Tính chất của hình thoi
- 2. Dấu hiệu nhận ra hình thoi
- 3. Công thức tính chu vi hình thoi
- 4. Công thức tính diện tích s quy hoạnh hình thoi
- 4.1. Công thức tính diện tích s quy hoạnh hình thoi nhờ vào cạnh đáy và độ cao
- 4.2. Công thức tính diện tích s quy hoạnh hình thoi nhờ vào hệ thức trong tam giác (Nếu biết góc)
- 5. Bài tập vận dụng
- 6. Công thức tính đường chéo
- 7. Cách chứng tỏ
- 8. Câu hỏi thường gặp
- 8.1. Hình vuông liệu có phải là hình thoi không?
- 8.2. Cách vẽ hình thoi GHIK chuẩn, nhanh gọn và vô cùng đơn thuần và giản dị
- Hình thoi là tứ giác có bốn cạnh bằng nhau.
- Hình thoi cũng khá sẽ là một hình bình hành.
- Một trong hai điểm lưu ý tạo ra sự độc lạ của hình thoi là bốn cạnh của nó có chiều dài bằng nhau, hay còn gọi là đồng dư. Đặc tính nhận dạng khác là những cạnh trái chiều tuy nhiên tuy nhiên với nhau.
- Nếu bạn có một tứ giác chỉ có một cặp cạnh tuy nhiên tuy nhiên thì đó chắc như đinh không còn hình thoi (vì hai cạnh của nó không thể có cùng độ dài). Đó là một hình thang .
- Nếu bạn có một tứ giác với hai cặp cạnh đối tuy nhiên tuy nhiên, đó hoàn toàn có thể có một hình bình hành. Nếu độ dài những cạnh bằng nhau thì đó chắc như đinh là hình “kim cương”.
- Các góc đối nhau sẽ có được độ lớn bằng nhau.
- Hai đường chéo của hình thoi sẽ vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Hai đường chéo là đường phân giác của những góc.
- Hình thoi có toàn bộ những tính chất của một hình bình hành.
- Tứ giác có bốn cạnh bằng nhau được gọi là hình “kim cương”.
- Tứ giác có 2 đường chéo là đường trung trực của nhau là “kim cương”.
- Tứ giác có 2 đường chéo là đường phân giác của toàn bộ bốn góc là “kim cương”.
- Hình thoi là một trường hợp đặc biệt quan trọng của một hình bình hành vì nó có khá đầy đủ tính chất của một hình bình hành và còn tồn tại một số trong những tính chất khác:
- Hình bình hành có hai cạnh bên bằng nhau là hình “kim cương”.
- Hình bình hành có hai tuyến phố chéo vuông góc với nhau là hình “kim cương”.
- Hình bình hành có một đường chéo là đường phân giác của một góc là hình “kim cương”.
- P là chu vi.
- a là chiều dài của cạnh.
- S là diện tích s quy hoạnh.
- d1 và d2 là hai tuyến phố chéo của hình “kim cương”.
- S là diện tích s quy hoạnh.
- d1 và d2 là độ dài 2 của đường chéo.
- Tứ giác có 4 cạnh bằng nhau.
- Hình bình hành là hình có hai cạnh kề bằng nhau.
- Hình bình hành là hình có hai tuyến phố chéo vuông góc với nhau.
- Hình bình hành là hình có một đường chéo là tia phân giác của một góc.
Trong hình học không khỏi phát hiện những hình rất khác nhau và nhất là hình thoi. Kiến thức về hình thoi không phải ai cũng nhớ. Bài viết này sẽ hỗ trợ bạn biết và củng cố thêm kiến thức và kỹ năng. Cùng theo dõi nhé!
1. Hình thoi là gì?
 Hình thoi là gì?
Hình thoi là gì?
Hình thoi là tứ giác có bốn cạnh bằng nhau và những cạnh trái chiều sẽ tuy nhiên tuy nhiên với nhau. Tất cả những hình thoi đều là hình bình hành, nhưng không phải toàn bộ những hình bình hành đều là hình thoi.
Tất cả những hình vuông vắn đều là hình thoi, nhưng không phải toàn bộ những hình thoi đều là hình vuông vắn. Các góc bên trong trái chiều của hình thoi là đồng dư. Các đường chéo của hình thoi luôn phân giác vuông góc với nhau.
1.1. Đặc điểm
1.2. Một hình thoi hoàn toàn có thể có ba tên tương hỗ update
Hình thoi
Lozenge
Kim cương
1.3. Tính chất của hình thoi
1.3.1. Tính chất về cạnh
1.3.2. Tính chất về góc
Ngoài bốn cạnh đó, hình thoi còn tồn tại bốn góc bên trong. Bạn cũng hoàn toàn có thể dựng hai tuyến phố chéo bên trong hình bằng phương pháp nối những đỉnh (góc) trái chiều.
Cho dù bạn sắp xếp bốn vật thể thẳng đó ra làm sao trên mặt phẳng, bạn sẽ luôn có hai cặp góc trái chiều bằng nhau. Nếu góc này là 30 độ thì góc trái chiều cũng tiếp tục là 30 độ..
1.3.3. Tính chất về đường chéo
Một tính chất tuyệt vời và hiếm có của hình thoi là những đường chéo của nó luôn vuông góc với nhau. Tạo một hình “kim cương” trên giấy tờ và nối hai cặp đỉnh trái chiều lại với nhau để tạo thành 2 đường chéo, bạn sẽ thấy được điều này. Các đường chéo luôn vuông góc với nhau.
Các đường chéo này cũng cắt nhau và cắt đúng chuẩn vào trung điểm. Hai đường chéo chia hình thoi thành bốn tam giác vuông.
Tính chất của hình thoi hoàn toàn có thể tóm gọn như sau:
2. Dấu hiệu nhận ra hình thoi
Có 2 tín hiệu để hoàn toàn có thể xác lập được đó là hình “kim cương”.
Hình tứ giác đặc biệt quan trọng
Hình bình hành đặc biệt quan trọng
3. Công thức tính chu vi hình thoi
Chu vi hình thoi được xem bằng công thức tổng độ dài những đường xung quanh hình, cũng đó đó là tổng độ dài đường xung quanh toàn bộ diện tích s quy hoạnh hình.
Để tính chu vi hình “kim cương”, ta tính tổng độ dài của 4 cạnh xung quanh.
Công thức tính chu vi hình “kim cương”:
P = a x 4
Trong số đó:
Ví dụ: Cho hình thoi ABCD có độ dài 4 cạnh bằng nhau và bằng 5 cm. Tìm chu vi?
Áp dụng công thức tính chu vi, ta có P = 5 x 4 = 20 cm.
4. Công thức tính diện tích s quy hoạnh hình thoi
Diện tích hình thoi được đo bằng độ lớn của mặt phẳng hình, là phần mặt phẳng ta hoàn toàn có thể nhìn thấy của nó.
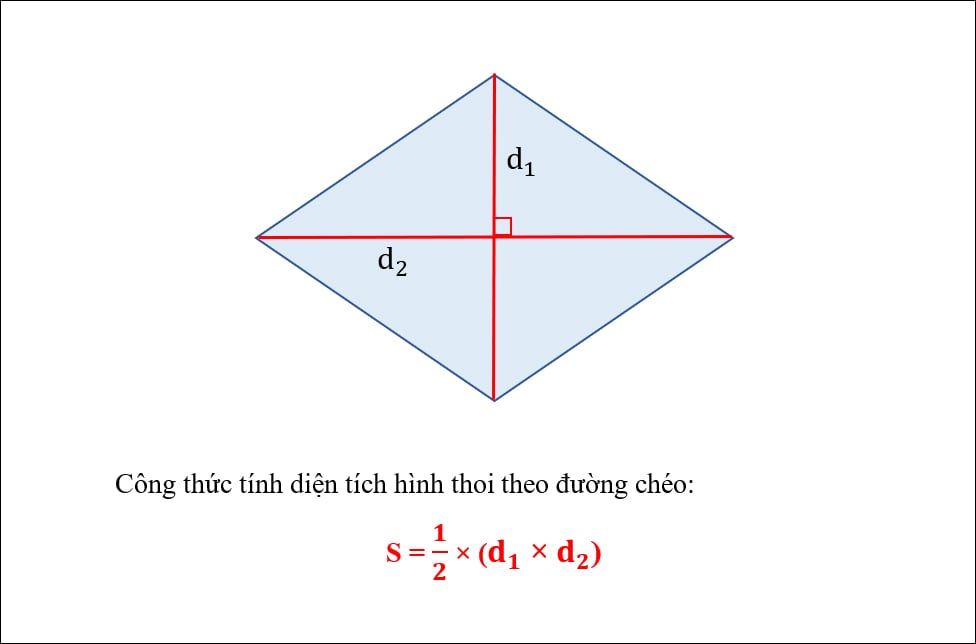
Diện tích của hình “kim cương” bằng một nửa tích độ dài của hai tuyến phố chéo.
Công thức tính diện tích s quy hoạnh hình “kim cương”:
SABCD = ½ (d1 x d2)
Trong số đó:
Ví dụ: Có một tấm bìa hình thoi, hai tuyến phố chéo của miếng bìa này còn có kích thước lần lượt là 4 cm, và 6 cm. Hỏi diện tích s quy hoạnh của tấm bìa đó bằng bao nhiêu?
Ta có d1 = 4 cm, d2 = 6 cm, vận dụng công thức tính diện tích s quy hoạnh hình “kim cương”:
SABCD = ½ (d1 x d2)
= ½ (4 x 6) = 12 cm2
Áp dụng theo công thức tính diện tích s quy hoạnh hình “kim cương”, ta có d1 = 6 cm và d2 = 8 cm. Áp dụng công thức và thay số, ta có kết quả như sau:
S = 1/2 x (d1 x d2) = 1/2 (6 x 8) = 1/2 x 48 = 24 cm2.
Vậy, tấm bìa có diện tích s quy hoạnh là 24 cm2.
4.1. Công thức tính diện tích s quy hoạnh hình thoi nhờ vào cạnh đáy và độ cao
S = h x a
Trong số đó:
– h: Chiều cao của hình “kim cương”.
– a: Cạnh đáy
Ví dụ: Cho hình thoi GHIK, có cạnh GH = HI = IK = KG = 5 cm, độ dài độ cao bằng 3 cm. Tính diện tích s quy hoạnh của hình GHIK.
Giải:
Ta có độ dài những cạnh a = 5 cm, độ cao h = 3 cm.
Áp dụng theo công thức diện tích s quy hoạnh S = h x a
= 3 x 5
= 15 cm2
Vậy, GHIK có diện tích s quy hoạnh là 15 cm2.
4.2. Công thức tính diện tích s quy hoạnh hình thoi nhờ vào hệ thức trong tam giác (Nếu biết góc)
Công thức: S = a2 sin A =a2 Sin B = a2 Sin C = a2 Sin D
Trong số đó:
Ví dụ: Cho hình thoi ABCD, có cạnh = 3 cm, góc B = 30 độ. Tính diện tích s quy hoạnh ABCD đó?
Giải:
Ta có a = 3 cm, góc B = 30 độ.
Áp dụng vào công thức S = a2 sin A = a2 Sin B = a2 Sin C = a2 Sin D
Ta tìm kiếm được S = (3)2 x sin (30) = 4,5 cm2
Vậy diện tích s quy hoạnh của hình ABCD là 4,5 cm2.
5. Bài tập vận dụng
Bài 1: Cho hình thoi ABCD có cạnh AB = 3 m, có góc BAD = 30 độ. Tính diện tích s quy hoạnh của hình ABCD.
Giải:
Do ABCD là hình thoi nên những tam giác tạo thành là tam giác cân, gọi I là trung điểm hai tuyến phố chéo AC và BD. Ta có AI vuông góc với BD vì vậy góc IAB = 15 độ.
Do đó, AI = AB x cos IAB = 3 x Cos 15 = 2,88 m.
Theo định lý Pytago, xét tam giác vuông ABI ta có:
BI2= AB2– AI2= 9 – 8,29 = 0,71
=> BI = 0,84 m
Ta có: AC = 2 x AI = 2 x 2,88 = 5,76 m
BD = 2 x BI = 2 x 0,84 = 1,68 m
Do đó, diện tích s quy hoạnh của hình ABCD = ½ x AC x BD = ½ x 5,76 x 1,68 = 4.83 (mét vuông)
Bài 2: Tính diện tích s quy hoạnh hình thoi ABCD, lúc biết độ dài cạnh AB = 6 cm, độ dài đường chéo AC = 8 cm.
Giải:
Gọi I là giao điểm của hai tuyến phố chéo AC và BD, ta có AI = IC = 4 cm
Xét tam giác vuông ABI, ta có:
BI2= AB2– AI2 = 36 – 16 = 20
=> BI = 4,4 cm.
Ta lại sở hữu BD = 2 x BI = 2 x 4,4 = 8,8 cm
Diện tích hình ABCD S = ½ (BD x AC) = ½ (8,8 x 8) = 35,2 cm2
6. Công thức tính đường chéo
Đường chéo là đường nối những đỉnh trái chiều của hình thoi lại với nhau. Hai đường chéo sẽ vuông góc với nhau tại giao điểm của chúng. Đường chéo là đại lượng quan trọng nhất để tìm ra diện tích s quy hoạnh hình “kim cương”. 2 đường chéo cắt nhau tại trung điểm mỗi đường đồng thời vuông góc với nhau được gọi là đường phân giác của mỗi góc.
Dựa vào những công thức tính chu vi và diện tích s quy hoạnh ở trên, toàn bộ chúng ta cũng hoàn toàn có thể thuận tiện và đơn thuần và giản dị tìm kiếm được công thức tính đường chéo như sau:
Tính độ dài đường chéo lúc biết diện tích s quy hoạnh và độ dài của một đường chéo còn sót lại
Từ công thức tính S = ½ ( d1 x d2 ) ta có công thức độ dài đường chéo như sau :
d1 = (S x 2) : d2 hoặc d2= (S x 2) : d1
Trong số đó:
Ví dụ: Cho hình thoi ABCD có độ dài cạnh bằng 10 cm, đường cao bằng 6 cm và AC<BD. Độ dài hai tuyến phố chéo AC và BD lần lượt là bao nhiêu?
Ta có SABCD = 10 x 6 = 60 cm2
Gọi độ dài hai tuyến phố chéo AC và BD lần lượt là a và b (a > b > 0)
Khi đó ½ ab = 60
⇔ 2ab = 240
Gọi giao điểm của 2 đường chéo AC và BD là O
Vì ABCD là hình thoi nên AC sẽ vuông góc với BD.
=> Tam giác AOB vuông tại O
=> AB2 = OA2 + OB2
Mà ta có OA = ½ b, OB = ½ a do tứ giác ABCD là hình thoi
Nên ¼ (a2 + b2) = 10 2
⇔ a2 + b2 = 400
Ta có:
a2 + b2 = 400 ⇔a2 + b2 + 2ab = 400 + 240 ⇔ (a + b)2 = 640 ⇔ a + b = 25
a2 + b2 = 400 ⇔ a2 + b2 – 2ab = 400 – 240 ⇔ (a – b)2 = 160 ⇔ a – b = 13
Giải hệ phương trình, tìm kiếm được a = 19, b = 6.
Vậy AC có độ dài là 19 và BD có độ dài là 6.
7. Cách chứng tỏ
Có 4 phương pháp để chứng tỏ một hình là hình “kim cương”
8. Câu hỏi thường gặp
8.1. Hình vuông liệu có phải là hình thoi không?
Nếu bạn có một hình thoi với bốn góc trong bằng nhau, bạn có một hình vuông vắn. Hình vuông là một trường hợp đặc biệt quan trọng của hình thoi, vì nó có bốn cạnh dài bằng nhau và có bốn góc vuông.
8.2. Cách vẽ hình thoi GHIK chuẩn, nhanh gọn và vô cùng đơn thuần và giản dị
Có 2 phương pháp để vẽ đó đó là thước kẻ – êke và thước kẻ – compa
Cách 1 : Vẽ bằng thước kẻ và êke
Bước 1: Vẽ đoạn thẳng GI bất kì và xác lập trung điểm O của đoạn thẳng GI đó.
Bước 2: Dùng êke vẽ đoạn thẳng HK vuông góc với GI tại O và nhận trung điểm O là trung điểm của HK.
Bước 3: Nối những đỉnh G với H, H với I, I với K, K với G => được hình thoi GHIK.
Cách 2 : Vẽ bằng thước kẻ và compa
Bước 1: Vẽ đoạn thẳng GI có độ dài bất kỳ.
Bước 2: Dùng compa, mở rộng độ mở compa to nhiều hơn 1/2 GI. Vẽ cung tròn tâm G và tâm I sao cho hai cung tròn cắt nhau tại hai điểm, hai giao điểm này gọi là H và K.
Bước 3: Nối những điểm G, H, I, K với nhau => được hình thoi GHIK.
Xem thêm:
Kết
Với những thông tin mà nội dung bài viết đã phục vụ về hình thoi, kỳ vọng hoàn toàn có thể giúp bạn biết thêm nhiều điều thú vị về nó. Có thể giúp ích được bạn trong học tập và hoàn toàn có thể vận dụng vào môi trường tự nhiên vạn vật thiên nhiên sống đời thường hằng ngày.
Chia Sẻ Link Cập nhật Ý nghĩa của hình thoi miễn phí
Bạn vừa tìm hiểu thêm tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Review Ý nghĩa của hình thoi tiên tiến và phát triển nhất và Share Link Cập nhật Ý nghĩa của hình thoi Free.

Hỏi đáp vướng mắc về Ý nghĩa của hình thoi
Nếu sau khi đọc nội dung bài viết Ý nghĩa của hình thoi vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha
#nghĩa #của #hình #thoi