Thủ Thuật về Tìm toàn bộ những giá trị thực của tham số để phương trình có nghiệm duy nhất x 1 Mới Nhất
Pro đang tìm kiếm từ khóa Tìm toàn bộ những giá trị thực của tham số để phương trình có nghiệm duy nhất x 1 được Update vào lúc : 2022-06-05 10:40:05 . Với phương châm chia sẻ Bí quyết Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Admin lý giải và hướng dẫn lại nha.
30/08/2022 518
Nội dung chính
- Đáp án cần chọn là: D
Phương trình đã cho có một nghiệm duy nhất lúc x2 − 3x + m = 0 vô nghiệm hoặc có nghiệm duy nhất x = 1.
TH1: Phương trình x2 − 3x + m = 0 vô nghiệm ⇔ Δ = 32 − 4m < 0 ⇔ m > 94 .
TH2: Phương trình x2 − 3x + m = 0 có nghiệm duy nhất x = 1
⇔Δ=012−3.1+m=0⇔9−4m=0−2+m=0⇔m=94m=2⇒m∈∅
Vậy m>94 - CÂU HỎI HOT CÙNG CHỦ ĐỀ
- Chuyên đề luyện thi vào 10: Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước
- I. Cách giải bài toán Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước
- II. Bài tập ví dụ bài toán Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước
- III. Bài tập tự luyện về bài toán Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước
- I. Cách giải bài toán Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước
- II. Bài tập ví dụ bài toán Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước
- III. Bài tập tự luyện về bài toán Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước
- Chuyên đề về Hệ phương trình lớp 9
- Toán nâng cao lớp 9 Chủ đề 5: Hệ phương trình
- Các dạng hệ phương trình đặc biệt quan trọng
- Chuyên đề 4: Giải bài Toán bằng phương pháp lập phương trình, hệ phương trình
- Rút gọn biểu thức – Xem thêm Ôn thi vào lớp 10 chuyên đề 1: Rút gọn và tính giá trị của biểu thức
- Hàm số đồ thị – Xem thêm Ôn thi vào lớp 10 chuyên đề 5: Hàm số và đồ thị
- Phương trình, hệ phương trình – Xem thêm Ôn thi vào lớp 10 chuyên đề 2: Giải phương trình và hệ phương trình số 1 hai ẩn
- Giải bài toán bằng phương pháp lập phương trình, hệ phương trình – Xem thêm Kỹ năng giải toán bằng phương pháp lập phương trình, hệ phương trình
- Hình học – Xem thêm Ôn thi vào lớp 10 chuyên đề 10: Chứng minh những hệ thức hình học
Đáp án cần chọn là: D
Phương trình đã cho có một nghiệm duy nhất lúc x2 − 3x + m = 0 vô nghiệm hoặc có nghiệm duy nhất x = 1.
TH1: Phương trình x2 − 3x + m = 0 vô nghiệm ⇔ Δ = 32 − 4m < 0 ⇔ m > 94 .
TH2: Phương trình x2 − 3x + m = 0 có nghiệm duy nhất x = 1
⇔Δ=012−3.1+m=0⇔9−4m=0−2+m=0⇔m=94m=2⇒m∈∅
Vậy m>94
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Tổng những nghiệm của phương trình |x2 + 5x + 4| = x + 4 bằng:
Xem đáp án » 28/08/2022 3,709
Tập nghiệm của phương trình 2x+3x−1=3xx−1 là:
Xem đáp án » 28/08/2022 3,035
Phương trình ax2 + bx + c = 0 (a ≠ 0). Phương trình có hai nghiệm dương phân biệt khi và chỉ khi:
Xem đáp án » 28/08/2022 2,537
Tập nghiệm của phương trình x2−4x−2x−2=x−2 là
Xem đáp án » 31/08/2022 2,176
Phương trình x−mx+1=x−2x−1 có nghiệm duy nhất lúc:
Xem đáp án » 30/08/2022 2,135
Cho phương trình (mét vuông − 3m + 2)x + mét vuông + 4m + 5 = 0. Tìm toàn bộ những giá trị thực của tham số m để phương trình đã cho có nghiệm đúng với mọi x thuộc R.
Xem đáp án » 28/08/2022 1,916
Tìm toàn bộ những giá trị thực của tham số m để phương trình
3×2 − 2(m + 1)x + 3m – 5 = 0 có một nghiệm gấp ba nghiệm còn sót lại.
Xem đáp án » 28/08/2022 1,615
Tìm toàn bộ những giá trị thực của tham số m để hai đồ thị hàm số y = −x2 − 2x + 3 và y = x2 − m có điểm chung.
Xem đáp án » 28/08/2022 1,572
Tập nghiệm của phương trình x−12x−3=−3x+1x+1 (1) là:
Xem đáp án » 31/08/2022 1,484
Cho phương trình (x − 1)(x2 − 4mx − 4) = 0 .Phương trình có ba nghiệm phân biệt khi:
Xem đáp án » 28/08/2022 1,415
Cho phương trình x4 + x2 + m = 0. Khẳng định nào sau này là đúng:
Xem đáp án » 30/08/2022 1,231
Nếu a, b, c, d là những số thực khác 0, biết c và d là nghiệm của phương trình x2 + ax + b = 0 và a, b là nghiệm của phương trình x2 + cx + d = 0 thì a + b + c + d bằng:
Xem đáp án » 28/08/2022 1,215
Cho phương trình ax4 + bx2 + c = 0 (1) (a ≠ 0). Đặt:
Δ = b2 − 4ac,S=−ba,P=ca . Khi đó (1) có 4 nghiệm phân biệt khi và chỉ khi:
Xem đáp án » 30/08/2022 1,196
Cho phương trình m−1×2+3x−1=0. Phương trình có nghiệm khi:
Xem đáp án » 28/08/2022 903
Cho hai phương trình x2 – mx + 2 = 0 và x2 + 2x – m = 0. Có bao nhiêu giá trị của m để một nghiệm của phương trình này và một nghiệm của phương trình kia có tổng là 3?
Xem đáp án » 28/08/2022 899
Tìm toàn bộ những giá trị của tham số m để phương trình x3 – 3×2 + 4 + m = 0 có nghiệm duy nhất to nhiều hơn 2. Biết rằng đồ thị của hàm số y = -x3 + 3×2 – 4 là hình bên
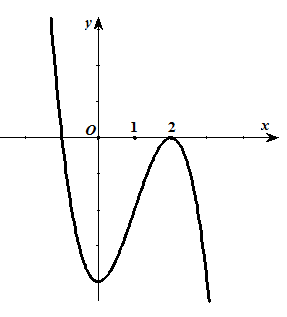
Giải thích :
Biến đổi x3 – 3×2 + 4 + m = 0 ⇔ – x3 + 3×2 – 4 = m
Dựa vào đồ thị hàm số để phương trình x3 – 3×2 + 4 + m = 0 có nghiệm duy nhất lơn hơn 2 thì m < -4.
Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước được VnDoc tổng hợp và chia sẻ xin gửi tới bạn đọc cùng tìm hiểu thêm. Các dạng bài tập tìm m toàn bộ chúng ta thường phát hiện những đề thi tuyển sinh vào lớp 10. Để nâng cao kỹ năng giải bài những em cùng tìm hiểu thêm những dạng bài toán tìm m để phương trình có nghiệm mà VnDoc tổng hợp dưới đây nhé. Mời những bạn cùng tìm hiểu thêm rõ ràng nội dung bài viết.
Chuyên đề luyện thi vào 10: Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước
Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước. Tài liệu này sẽ hỗ trợ ích cho những em rèn luyện làm quen với những dạng bài tập tìm m để hệ phương trình có nghiệm từ đó sẵn sàng sẵn sàng tốt cho kì thi cuối cấp cũng như kì thi vào lớp 10 sắp tới đây. Chúc những em ôn tập tốt
I. Cách giải bài toán Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước
+ Bước 1: Đặt Đk để hệ phương trình có nghĩa (nếu có)
+ Bước 2: Tìm Đk để hệ phương trình có nghiệm duy nhất
+ Bước 3: Giải hệ phương trình tìm nghiệm (x; y) theo tham số m
+ Bước 4: Thay nghiệm (x; y) vừa tìm kiếm được vào biểu thức Đk
+ Bước 5: Giải biểu thức Đk để tìm m, kết phù thích hợp với Đk để hệ phương trình có nghiệm duy nhất.
+ Bước 6: Kết luận
II. Bài tập ví dụ bài toán Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước
Bài 1: Cho hệ phương trình
a, Tìm m để hệ phương trình có nghiệm duy nhất

b, Tìm m để hệ phương trình có nghiệm x < 0; y > 0
Lời giải:
a, Để hệ phương trình có nghiệm duy nhất
 ⇔ m ≠ 3
⇔ m ≠ 3
b, Với m ≠ 3, hệ phương trình có nghiệm duy nhất
Theo đề bài, ta có:

Để y > 0
 ⇒ m – 3 > 0 ⇔ m > 3
⇒ m – 3 > 0 ⇔ m > 3
Để x < 0 khi và chỉ khi

Vậy với 3 < m < 4 thì hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu x < 0 và y > 0
Bài 2: Tìm m nguyên để hệ phương trình sau có nghiệm duy nhất và là nghiệm nguyên:

Lời giải:
Với m = 0 hệ phương trình trở thành
 (loại do những nghiệm nguyên)
(loại do những nghiệm nguyên)
Với m khác 0, để hệ phương trình có nghiệm duy nhất
 ⇔ mét vuông ≠ 4 ⇔ m ≠ ± 2, kết phù thích hợp với Đk m ≠ 0 ⇒ m ≠ 0 và m ≠ ± 2
⇔ mét vuông ≠ 4 ⇔ m ≠ ± 2, kết phù thích hợp với Đk m ≠ 0 ⇒ m ≠ 0 và m ≠ ± 2
Vậy với m ≠ 0 và m ≠ ± 2 thì hệ phương trình có nghiệm duy nhất
Ta có:


Để x nguyên

Để y nguyên

Vậy để x, y nguyên thì m + 2 ∈ Ư(3) = -3; -1; 1; 3
Ta có bảng:
m + 5-3-113m-5 ™-2 (loại)-1 ™1 ™
Vậy với m ∈ -5; -1; 1 thì hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu những nghiệm nguyên
Bài 3: Cho hệ phương trình
 . Tìm m để hệ phương trình có nghiệm (x; y) sao cho biểu thức P = xy + 2(x + y) đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
. Tìm m để hệ phương trình có nghiệm (x; y) sao cho biểu thức P = xy + 2(x + y) đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Lời giải:


Để hệ phương trình có nghiệm khi và chỉ khi phương trình (2) có nghiệm
⇔ ∆ ≥ 0 ⇔ -3m2 + 12 0 ⇔ mét vuông – 4 ≤ 0 ⇔ (m – 2)(m + 2) ≤ 0

Vậy với -2 ≤ m ≤ 2 thì hệ phương trình có nghiệm.
Ta cóP = xy + 2 (x + y) = mét vuông – 3 + 2m = (m + 1)2 – 4 ≥ – 4
Dấu “=” xảy ta khi m = -1 (thỏa mãn nhu cầu)
Vậy min P = -4 khi m = -1
III. Bài tập tự luyện về bài toán Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước
Bài 1: Cho hệ phương trình:
 . Tìm m để hệ phương trình có nghiệm duy nhất sao cho những nghiệm đều nguyên
. Tìm m để hệ phương trình có nghiệm duy nhất sao cho những nghiệm đều nguyên
Bài 2: Cho hệ phương trình:
 . Tìm m để hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn nhu cầu 3x – y = 1
. Tìm m để hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn nhu cầu 3x – y = 1
Bài 3: Cho hệ phương trình
 . Tìm m để hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn nhu cầu 2x + y = 9
. Tìm m để hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn nhu cầu 2x + y = 9
Bài 4: Cho hệ phương trình
 . Tìm m để hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn nhu cầu x = |y|.
. Tìm m để hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn nhu cầu x = |y|.
Bài 5: Cho hệ phương trình
 . Tìm m để hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn nhu cầu
. Tìm m để hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn nhu cầu
a, x và y trái dấu
b, x và y cùng dương
Bài 6: Cho hệ phương trình
 . Tìm m để hệ phương trình có nghiệm duy nhất (x; y) sao cho P = x.y đạt giá trị lớn số 1
. Tìm m để hệ phương trình có nghiệm duy nhất (x; y) sao cho P = x.y đạt giá trị lớn số 1
Bài 7: Cho hệ phương trình
 . Tìm m để hệ phương trình có nghiệm duy nhất (x; y) sao cho A = x2 + y2đạt giá trị nhỏ nhất
. Tìm m để hệ phương trình có nghiệm duy nhất (x; y) sao cho A = x2 + y2đạt giá trị nhỏ nhất
Ngoài ra, VnDoc.com đã xây dựng group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 9. Mời những bạn học viên tham gia nhóm, để hoàn toàn có thể nhận được những tài liệu tiên tiến và phát triển nhất.
Như vậy VnDoc đã chia sẻ cho những em bài Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước. Chắc hẳn qua nội dung bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức và kỹ năng của bài học kinh nghiệm tay nghề rồi đúng không ạ ạ? Bài viết cho toàn bộ chúng ta thấy được cách tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước, cách giải bài toán tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn nhu cầu Đk cho trước, những bài tập ví dụ và tự luyện về bài toán tìm m… Hy vọng với tài liệu này những em sẽ thuận tiện và đơn thuần và giản dị hoàn thành xong bài tập mà giáo viên giao cho, nâng cao điểm số trong bài kiểm tra sắp tới này cũng như sẵn sàng sẵn sàng tốt cho kì thi vào lớp 10. Chúc những em học tốt, để nâng cao kỹ năng giải bài Toán lớp 9, những em cùng tìm hiểu thêm những dạng bài tập nâng cao dưới đây nhé.
——————-
Ngoài những dạng Toán 9 ôn thi vào lớp 10 trên, để giúp bạn đọc có thêm nhiều tài liệu học tập hơn thế nữa, VnDoc.com mời những bạn học viên còn tồn tại thể tìm hiểu thêm thêm tài liệu những đề thi học kì 2 lớp 9 những môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và tinh lọc. Với tài liệu này giúp những bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn, thông qua đó giúp những bạn học viên ôn tập, sẵn sàng sẵn sàng tốt vào kì thi tuyển sinh lớp 10 sắp tới đây. Chúc những bạn ôn thi tốt!
Các dạng bài tập Toán 9 ôn thi vào lớp 10 là tài liệu tổng hợp 5 chuyên đề lớn trong chương trình Toán lớp 9, gồm có:
Để giúp những bạn hoàn toàn có thể giải đáp được những vướng mắc và vấn đáp được những vướng mắc khó trong quy trình học tập, VnDoc.com mời bạn đọc cùng đặt vướng mắc tại mục hỏi đáp học tập của VnDoc nhé. Chúng tôi sẽ tương hỗ vấn đáp trong thời hạn sớm nhất.




Chia Sẻ Link Cập nhật Tìm toàn bộ những giá trị thực của tham số để phương trình có nghiệm duy nhất x 1 miễn phí
Bạn vừa đọc nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Review Tìm toàn bộ những giá trị thực của tham số để phương trình có nghiệm duy nhất x 1 tiên tiến và phát triển nhất và Share Link Cập nhật Tìm toàn bộ những giá trị thực của tham số để phương trình có nghiệm duy nhất x 1 Free.

Giải đáp vướng mắc về Tìm toàn bộ những giá trị thực của tham số để phương trình có nghiệm duy nhất x 1
Nếu sau khi đọc nội dung bài viết Tìm toàn bộ những giá trị thực của tham số để phương trình có nghiệm duy nhất x 1 vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha
#Tìm #tất #cả #những #giá #trị #thực #của #tham #số #để #phương #trình #có #nghiệm #duy #nhất