Mẹo về Cách tính đường cao trong tam giác vuông lớp 7 Chi Tiết
Pro đang tìm kiếm từ khóa Cách tính đường cao trong tam giác vuông lớp 7 được Cập Nhật vào lúc : 2022-07-20 14:20:05 . Với phương châm chia sẻ Mẹo về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Nội dung chính
- Bài tập Tam giác cân, tam giác vuông cân lớp 7
- I. Định nghĩa về tam giác cân
- II. Tính chất của tam giác cân
- III. Công thức tính Diện tích Tam giác cân
- IV. Định nghĩa về tam giác vuông cân
- V. Tính chất của tam giác vuông cân
- VI. Công thức tính trung tuyến tam giác vuông cân
- VII. Tam giác đều
- Đường cao trong tam giác là gì?
- Công thức tính đường cao trong tam giác thường
- Công thức tính đường cao trong tam giác vuông
- Công thức tính đường cao trong tam giác đều
- Công thức tính đường cao trong tam giác cân
- S: Diện tích của hình tam giác.
- a: Cạnh đáy tương ứng với độ cao của hình tam giác.
- h: Chiều cao của tam giác.
- h: Chiều cao của tam giác.
- b. c: Độ dài những cạnh của hình tam giác.
- a: Cạnh đáy tương ứng với độ cao của hình tam giác
- p.: Nửa chu vi của hình tam giác.
- a2 = b2 + c2
- b2 = a.b′ và c2 = a.c′
- a.h = b.c
- h2 = b′.c′
- 1/h2=1/b2+1/c2
- a, b, c: độ dài những cạnh của tam giác vuông.
- b’: đường chiếu của cạnh b ứng trên cạnh huyền.
- c’: đường chiếu của cạnh c ứng trên cạnh huyền.
- h: đường cao hạ từ đỉnh góc vuông.
- h: Chiều cao của tam giác đều.
- a: Cạnh của tam giác đều.
Thế nào là tam giác cân và tam giác vuông cân, phân biệt hai tam giác này ra làm sao? Mời những bạn tìm hiểu thêm tài liệu Định nghĩa hình tam giác cân, tam giác vuông cân do kienthucnews.com sưu tầm và đăng tải sau này. Hy vọng đây sẽ là tài liệu hữu ích cho những em học viên lớp 7 ôn tập và nâng cao kiến thức và kỹ năng môn Toán lớp 7.
Bạn đang xem: Đường cao của tam giác vuông cân
Bài tập Tam giác cân, tam giác vuông cân lớp 7
I. Định nghĩa về tam giác cân
Tam giác cân là tam giác có hai cạnh bằng nhau, hai cạnh này được gọi là hai cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn sót lại gọi là góc ở đáy
Ở hình trên, tam giác ABC có AB = AC suy ra tam giác ABC cân.
Có AB và AC là hai cạnh bên nên tam giác ABC cân tại đỉnh A.
II. Tính chất của tam giác cân
Tính chất 1: Trong một tam giác cân hai góc ở đáy bằng nhau.
Chứng minh:
Giả thiết Tam giác ABC cân tại A, AB = AC Kết luận

Trong tam giác cân ABC, gọi AM là tia phân giác của góc

Khi đó ta có

Xét tam giác ABM và tam giác ACM có:
AB = AC (gt)
 (cmt)
(cmt)
AM chung
Suy ta
 (c.g.c)
(c.g.c)
 (đpcm)
(đpcm)
Tính chất 2: Một tam giác có hai góc bằng nhau thì là tam giác cân.
Chứng minh
Giả thiết Tam giác ABC,
 Kết luận Tam giác ABC cân tại A
Kết luận Tam giác ABC cân tại A
Trong tam giác ABC, gọi AM là tia phân giác của

Tam giác ABM có
 (tổng 3 góc trong một tam giác)
(tổng 3 góc trong một tam giác)
Tam giác ACM có
 (tổng 3 góc trong một tam giác)
(tổng 3 góc trong một tam giác)
Mà lại sở hữu

nên

Xét tam giác ABM và tam giác ACM có:



Suy ra
 nên AB = AC (cạnh tương ứng bằng nhau)
nên AB = AC (cạnh tương ứng bằng nhau)
Xét tam giác ABC có AB = AC, suy ra tam giác ABC cân tại A (định nghĩa)
Tính chất 3: Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường cao của tam giác đó.
Tính chất 4: Trong một tam giác, nếu có một đường trung tuyến đồng thời là đường trung trực thì tam giác là tam giác cân.
Dấu hiệu nhận ra tam giác cân:
Dấu hiệu 1: Nếu một tam giác có hai cạnh bên bằng nhau thì tam giác đó là tam giác cân.
Dấu hiệu 2: Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
III. Công thức tính Diện tích Tam giác cân
– Diễn giải: Diện tích tam giác cân đối Tích của độ cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, tiếp theo đó chia cho 2.
– Công thức tính diện tích s quy hoạnh tam giác cân: S = (a x h)/ 2
+ a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)+ h: Chiều cao của tam giác (độ cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
IV. Định nghĩa về tam giác vuông cân
Tam giác vuông cân vừa là tam giác vuông, vừa là tam giác cân hay nói cách khác tam giác vuông là tam giác có 2 cạnh vuông góc và bằng nhau.
Xem thêm: Tranh Tô Màu Bánh Trung Thu Dành Tặng Cho Bé, Tranh Tô Màu Trung Thu Cho Bé Đẹp Nhất 2022
Tam giác ABC có AB = AC, AB ⊥ AC thì tam giác ABC vuông cân tại A.
V. Tính chất của tam giác vuông cân
Tính chất 1: Tam giác vuông cân có hai góc nhọn ở đáy bằng nhau và bằng 450
Chứng minh:
Xét tam giác vuông cân ABC cân tại A.
Vì ABC là tam giác cân nên
 =
=

ABC vuông nên


Mặt khác:

Tính chất 2: Các đường cao, đường trung tuyến, đường phân giác kẻ từ đỉnh góc vuông của tam giác vuông cân trùng nhau và bằng 1 nửa cạnh huyền.
Ví dụ: Xét tam giác ABC vuông cân tại A. Gọi D là trung điểm của BC. Ta có AD vừa là đường cao, vừa là đường phân giác, vừa là trung tuyến của BC.
AD = BD = DC =
 BC
BC
Cách chứng tỏ tam giác vuông cân:
Ta chứng tỏ một tam giác có:
+ Hai cạnh góc vuông bằng nhau.
+ Tam giác vuông có một góc bằng

+ Tam giác cân có một góc ở đáy bằng

VI. Công thức tính trung tuyến tam giác vuông cân
Tam giác vuông cân là một tam giác có một góc vuông với hai cạnh góc vuông bằng nhau và bằng a. Do đó, trung tuyến trong tam giác vuông cân mà nối từ góc vuông đến cạnh trái chiều sẽ là một đoạn thẳng vuông góc với cạnh huyền và bằng một phần hai nó.
Vì đấy là một tam giác đặc biệt quan trọng nên những tính chất trong tam giác vuông cân khá đơn thuần và giản dị. Nhưng với tam giác thường, những tính chất sẽ phức tạp hơn. Và những tính đó ra làm sao, những bạn hãy tìm hiểu thêm tài liệu phía dưới nhé.
VII. Tam giác đều
Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau.
Tính chất: Trong tam giác đều:
+ Ba cạnh tam giác bằng nhau.
+ Ba góc bằng nhau và bằng
 .
.
+ Có tính chất đường cao, đường trung tuyến, đường phân giác, đường trung trực in như tam giác cân.
Hệ quả: Trong một tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau.
Dấu hiệu nhận ra:
Nếu trong một tam giác có ba cạnh bằng nhau thì đó là tam giác đều. Nếu trong một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều. Nếu trong một tam giác cân có một góc bằng
 thì tam giác đó là tam giác cân.
thì tam giác đó là tam giác cân.
———————
Chuyên đề về tam giác là một nội dung được học trong chương trình Toán 7 học kì 2. Đây cũng là phần kiến thức và kỹ năng thường xuất hiện trong những bài thi, bài kiểm tra môn Toán lớp 7, chính vì vậy việc nắm vững những kiến thức và kỹ năng về tam giác là rất quan trọng giúp những em học viên hoàn toàn có thể đạt điểm trên cao trong những bài thi của tớ. Hy vọng tài liệu trên sẽ hỗ trợ những em học viên ghi nhớ lý thuyết về tam giác từ đó vận dụng giải những bài toán về tam giác một cách thuận tiện và đơn thuần và giản dị hơn. Chúc những em học tốt.
Để tiện trao đổi, chia sẻ kinh nghiệm tay nghề về giảng dạy và học tập những môn học lớp 7, kienthucnews.com mời những thầy cô giáo, những bậc phụ huynh và những bạn học viên truy vấn nhóm riêng dành riêng cho lớp 7 sau: Nhóm Tài liệu học tập lớp 7. Rất mong nhận được sự ủng hộ của những thầy cô và những bạn.
Trong nội dung bài viết dưới đây, THPT CHUYÊN LAM SƠN sẽ chia sẻ lý thuyết và công thức tính đường cao trong tam giác thường, vuông, đều và cân kèm theo những dạng bài tập có lời giải rõ ràng để những bạn cùng tìm hiểu thêm nhé.
Đường cao trong tam giác là gì?
Đường cao trong tam giác là đường thẳng từ đỉnh tam giác hạ vuông góc xuống cạnh trái chiều. Trong một tam giác có 3 đường cao và chúng đồng quy với nhau tại 1 điểm.
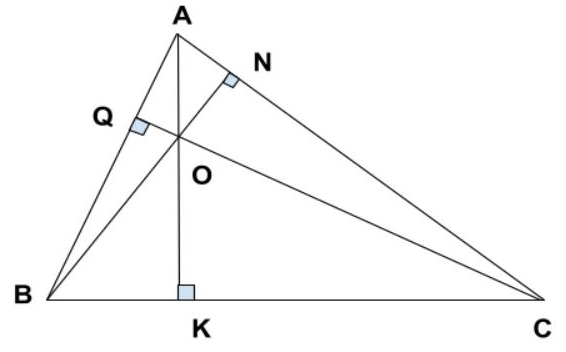
Công thức tính đường cao trong tam giác thường
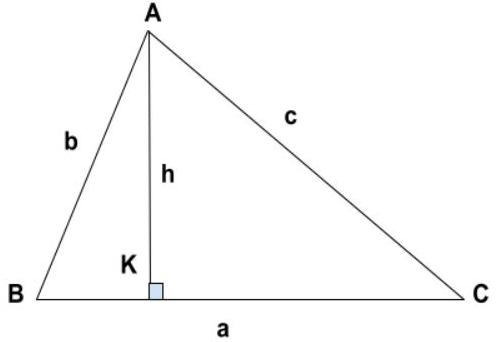
Cách tính đường cao của một tam giác bằng diện tích s quy hoạnh tam giác nhân 2 rồi chia cho cạnh đáy tương ứng với độ cao đó
h = S.a
Trong số đó:
Cách tính đường cao của một tam giác ta hoàn toàn có thể sử dụng công thức Heron đã được chứng tỏ:
ha = 2.[√p.(p – a)(p – p)(p – c)]/2
Trong số đó:
Ví dụ: Giả sử những bạn có tam giác ABC cân tại A, đường cao AH vuông góc tại H như sau:Cho tam giác ABC, cạnh AB = 4 cm, cạnh BC = 7 cm, cạnh AC = 5 cm. Tính đường cao AH Tính từ lúc A cắt BC tại H và tính diện tích s quy hoạnh ABC.
Lời giải
Nửa chu vi tam giác : P = ( AB+BC+AC):2 = ( 4+7+5):2 = 8 cm
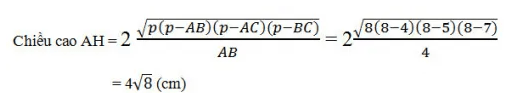
Xét tam giác ABC ta có:
SABC= ½AH.BC = ½4√8.7 = 14√8 cm2
Như vậy, AH = 4√8 cm, SABC = 14√8 cm2
Tham khảo thêm:
Công thức tính đường cao trong tam giác vuông
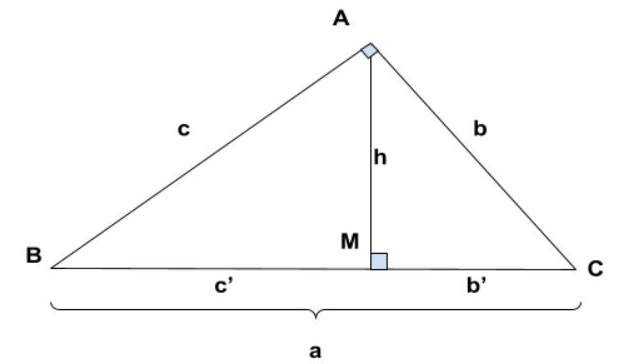
Áp dụng công thức tính cạnh và đường cao trong tam giác vuông, ta có công thức tính đường cao trong tam giác vuông là:
Trong số đó:
Ví dụ: Cho tam giác ABC vuông tại A, có đường cao AH, biết AB : AC = 3; AB + AC = 21cm.
a. Tính độ dài những cạnh của tam giác ABC.
b. Tính đường cao AH.
Lời giải
Theo giả thiết: AB:AC = 3:4
AB/AC = 3/4 ⇔ AB = 3AC/4
Trong khi: AB + AC = 21 ⇔ 3AC/4 + AC = 21⇔ AC = 12 cm
⇒ AB = 9 cm
Theo định lý pytago: BC2 = AB2 + AC2 = 92 + 122 = 225
⇒ BC = 15 cm
Như vậy AB = 9 cm, BC = 15 cm, AC = 12 cm
b. Tam giác vuông ABC vuông tại A nên ta có:
AH.BC = AB.AC
AH = (AB.AC)/BC = (9.12)/15 = 7,2 cm
Như vậy đường cao AH = 7,2 cm
Công thức tính đường cao trong tam giác đều
Đường cao tam giác đều phải có độ dài bằng nhau, vận dụng định lý Heron ta có công thức tính đường cao trong tam giác đều
h = a√3/2
Trong số đó:
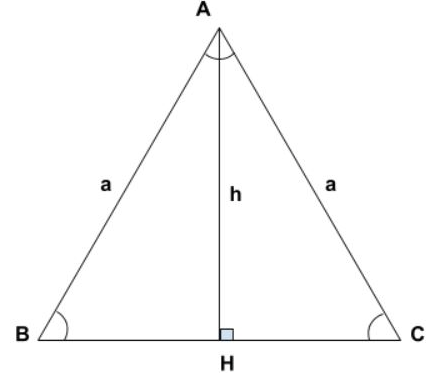
Công thức tính đường cao trong tam giác cân
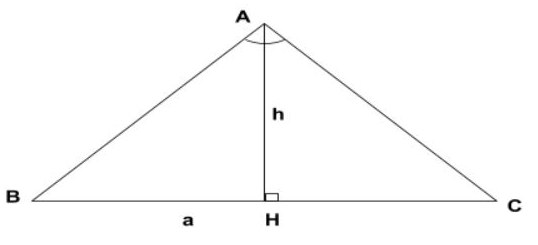
Ta có a là độ dài 2 cạnh băng nhau của tam giác cân, b là độ dài cạnh còn sót lại, ha là độ dài đường cao trong tam giác cân
Áp dụng định lý Pytago ta có: a2 = (b/2)2 + h2
Từ đó ta có công thức tính đường cao của tam giác cân là
h2 = a2 – (b/2)2 ⇒ h = √[a2 – (b/2)2]
Ví dụ: Tính chiều dài đường cao trong tam giác cân có độ dài 2 cạnh bằng nhau là 2cm và độ dài cạnh còn sót lại là 3
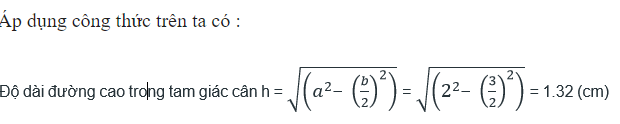
Hy vọng với những kiến trên về công thức tính đường cao trong tam giác thường, vuông, cân, đều hoàn toàn có thể giúp bạn vận dụng vào làm bài tập nhanh gọn




Share Link Download Cách tính đường cao trong tam giác vuông lớp 7 miễn phí
Bạn vừa đọc tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Clip Cách tính đường cao trong tam giác vuông lớp 7 tiên tiến và phát triển nhất và ShareLink Tải Cách tính đường cao trong tam giác vuông lớp 7 miễn phí.

Hỏi đáp vướng mắc về Cách tính đường cao trong tam giác vuông lớp 7
Nếu sau khi đọc nội dung bài viết Cách tính đường cao trong tam giác vuông lớp 7 vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha
#Cách #tính #đường #cao #trong #tam #giác #vuông #lớp