Mẹo về Cho tam giác abc, đường trung tuyến am qua điểm d thuộc cạnh bc 2022
Bạn đang tìm kiếm từ khóa Cho tam giác abc, đường trung tuyến am qua điểm d thuộc cạnh bc được Update vào lúc : 2022-07-05 22:20:03 . Với phương châm chia sẻ Kinh Nghiệm Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha.
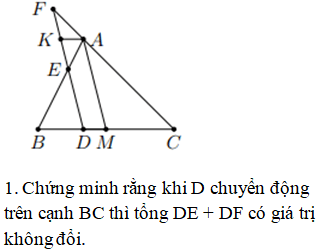
Môn Toán Lớp 8 Cho tam giác ABC, đường trung tuyến AM. Qua điểm D thuộc cạnh BC Ê Vẽ đường thẳng tuy nhiên tuy nhiên với AM cắt AB và AC làm được tại E và F.
a) Chứng minh DE+DF=2AM
b) đường thẳng A tuy nhiên tuy nhiên với BC cắt EF tại N. Chứng minh N là trung điểm của EF
c) Chứng minh S^2 FDC > hoặc=16 S AMC. S FNA
Giúp em bài này với ạ em cần gấp, đừng copy nguồn trên mạng nha. Em xin cảm ơn thầy cô và những bạn nhiều.
Câu hỏi: Cho tam giác ABC, đường trung tuyến AM. Qua điểm D thuộc cạnh BC, vẽ đường thẳng tuy nhiên tuy nhiên với AM, cắt AB và AC theo thứ tự ở E và F.
Lorem ipsum dolor sit amet, consectetur adipiscing elit.Morbi adipiscing gravdio, sit amet suscipit risus ultrices eu.Fusce viverra neque purus laoreet consequa.Vivamus vulputate posuere nisl quis consequat.

Khách
Hãy nhập vướng mắc của bạn vào đây
Những vướng mắc liên quan
Cho tam giác ABC, đường trung tuyến AM. Qua điểm D thuộc cạnh BC, vẽ đường thẳng tuy nhiên tuy nhiên với AM cắt AB và AC lần lượt tại Evà F.
a, Chứng minh DE+DF=2AM.
b, Đường thẳng qua A tuy nhiên tuy nhiên với BC cắt EF tại N. Chứng minh N là trung điểm của EF.
Cho tam giác ABC, trung tuyến AM. Qua điểm D thuộc cạnh BC, vẽđường thẳng tuy nhiên tuy nhiên với AM, cắt AB, AC tại E và F
a)Chứng minh DE + DF không đổi khi D di động trên BC
b) Qua A vẽ đường thẳng tuy nhiên tuy nhiên với BC, cắt FE tại K. Chứng minh rằng K là trung điểm của FE
Hãy luôn nhớ cảm ơn và vote 5*
nếu câu vấn đáp hữu ích nhé!
khangvo757 rất mong câu vấn đáp từ bạn. Viết vấn đáp

XEM GIẢI BÀI TẬP SGK TOÁN 8 – TẠI ĐÂY


CÂU HỎI HOT CÙNG CHỦ ĐỀ
Cho tam giác ABC cân tại A có BC = 2a, M là trung điểm của BC. Lấy những điểm D, E theo thứ tự thuộc những cạnh AB, AC sao cho DME^=B^
1. Chứng minh rằng tích BC.CE không đổi
2. Chứng minh rằng DM là tia phân giác của góc BDE
3. Tính chu vi tam giác AED nếu tam giác ABC là tam giác đều.
Xem đáp án » 17/01/2022 3,231
Cho tam giác ABC (AB < AC) đường phân giác AD. Đường trung trực của AD cắt BC ở K.
1. Chứng minh rằng △KAB=△KCA
2. Tính độ dài KD biết BD = 2 cm, DC = 4 cm
Xem đáp án » 17/01/2022 3,047
Cho hình thoi ABCD cạnh a có A^=60°. Một đường thẳng bất kì trải qua C cắt tia đối của những tia BA và DA theo thứ tự tại M và N.
1, Chứng minh rằng tích BM. DN có mức giá trị không đổi
2, Gọi K là giao điểm của BN và DM. Tính góc BKD.
Xem đáp án » 17/01/2022 2,937
Cho hình vuông vắn ABCD, O là giao điểm của hai tuyến phố chéo. Lấy điểm G thuộc cạnh BC, điểm H thuộc cạnh CD sao cho GOH^=45°. Gọi M là trung diểm của AB. Chứng minh rằng:
1. Tam giác HOD đồng dạng với tam giác OGB
2. MG tuy nhiên tuy nhiên vơi AH.
Xem đáp án » 17/01/2022 2,675
Cho tam giác ABC cân tại A, đường phân giác BD. Tính độ dài BD biết rằng BC = 5 cm, AC = 20 cm.
Xem đáp án » 17/01/2022 2,596
Các đường phân giác những góc ngoài tại những đỉnh B và C của tam giác ABC cắt nhau ở K. Đường thẳng vuông góc với AK tại K cắt những đường thẳng AB, AC theo thứ tự ở D, E. Chứng minh rằng
1. Các tam giác BDK và EKC đồng dạng
2. DE2=4BD.CE
Xem đáp án » 17/01/2022 2,399




Share Link Down Cho tam giác abc, đường trung tuyến am qua điểm d thuộc cạnh bc miễn phí
Bạn vừa tìm hiểu thêm nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Video Cho tam giác abc, đường trung tuyến am qua điểm d thuộc cạnh bc tiên tiến và phát triển nhất và Chia Sẻ Link Cập nhật Cho tam giác abc, đường trung tuyến am qua điểm d thuộc cạnh bc miễn phí.

Thảo Luận vướng mắc về Cho tam giác abc, đường trung tuyến am qua điểm d thuộc cạnh bc
Nếu sau khi đọc nội dung bài viết Cho tam giác abc, đường trung tuyến am qua điểm d thuộc cạnh bc vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Ad lý giải và hướng dẫn lại nha
#Cho #tam #giác #abc #đường #trung #tuyến #qua #điểm #thuộc #cạnh