Kinh Nghiệm về Hướng dẫn one proportion z test in python – kiểm tra một tỷ suất z trong python Mới Nhất
You đang tìm kiếm từ khóa Hướng dẫn one proportion z test in python – kiểm tra một tỷ suất z trong python được Cập Nhật vào lúc : 2022-10-28 03:00:10 . Với phương châm chia sẻ Kinh Nghiệm về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Admin lý giải và hướng dẫn lại nha.
Một thử nghiệm Z tỷ suất được sử dụng để so sánh tỷ suất quan sát được với tỷ suất lý thuyết.
Nội dung chính Show
- Một tỷ suất z-test trong python
- Ví dụ: Một tỷ suất Z-Test trong Python
- Tài nguyên tương hỗ update
- Phương pháp 1: Tính toán & NBSP; Bài kiểm tra Z theo tỷ suất sử dụng Công thức
- Phương pháp 2: Tính toán & nbsp; Phân tích Z theo tỷ suất
- Làm thế nào để bạn thực thi một tỷ suất z
- Làm thế nào để bạn làm một tỷ suất z
- Làm thế nào để bạn thực thi một bài kiểm tra tỷ suất trong Python?
- Bài kiểm tra tỷ suất 1 là gì?
Bài kiểm tra này sử dụng những giả thuyết null sau:
- H0: & nbsp; p. = p0 (tỷ suất dân số bằng với tỷ suất giả thuyết P0)p. = p0 (population proportion is equal to hypothesized proportion p0)
Giả thuyết thay thế hoàn toàn có thể là hai đuôi, đuôi trái hoặc đuôi phải:
- H1 & nbsp; (hai đuôi): & nbsp; p. & nbsp; ≠ p0 & nbsp; (tỷ suất dân số không bằng một số trong những giá trị giả thuyết P0)p. ≠ p0 (population proportion is not equal to some hypothesized value p0)
- H1 & nbsp; (đuôi trái): & nbsp; p. p.
- H1 & nbsp; (đuôi phải): & nbsp; p.> p0 & nbsp; (tỷ suất dân số to nhiều hơn một số trong những giá trị giả thuyết P0)p.
> p0 (population proportion is greater than some hypothesized value p0)
Thống kê kiểm tra sẽ là:
z = (p.-p0) / p0 (1-p0) / np0(1-p0)/n
where:
- p.: & nbsp; quan sát & nbsp; tỷ suất mẫuobserved sample proportion
- P0: & NBSP; Tỷ lệ dân số được đưa ra giả thuyết hypothesized population proportion
- n: & nbsp; cỡ mẫusample
size
Nếu giá trị p. tương ứng với Thống kê thử nghiệm Z nhỏ hơn mức ý nghĩa đã chọn của bạn (những lựa chọn chung là 0,10, 0,05 và 0,01) thì bạn hoàn toàn có thể từ chối giả thuyết khống.
Một tỷ suất z-test trong python
Để thực thi một thử nghiệm Z tỷ suất trong Python, toàn bộ chúng ta hoàn toàn có thể sử dụng hàm Tỷ lệ_ztest () từ thư viện & nbsp; StatSmodels, sử dụng cú pháp sau:statsmodels library, which uses the following syntax:
Tỷ lệ_ztest (đếm, nobs, value = none, thay thế = hai mặt hai mặt) & nbsp;
where:
- Đếm: Số lượng thành công xuất sắcThe number of successes
- Nobs: Số lượng thử nghiệmThe number of trials
- Giá trị: Tỷ lệ dân số được đưa ra giả thuyếtThe hypothesized population proportion
- Thay thế: & NBSP; Giả thuyết thay thếThe alternative hypothesis
Hàm này trả về một thử nghiệm z và giá trị p. tương ứng.
Ví dụ sau này đã cho toàn bộ chúng ta biết cách sử dụng hiệu suất cao này để thực thi một thử nghiệm Z tỷ suất trong Python.
Ví dụ: Một tỷ suất Z-Test trong Python
Giả sử chúng tôi muốn biết liệu tỷ suất dân cư ở một quận nhất định tương hỗ một luật nhất định bằng 60%. Để kiểm tra điều này, chúng tôi tích lũy tài liệu sau trên một mẫu ngẫu nhiên:
- P0: & NBSP; Tỷ lệ dân số giả thuyết = 0,60 hypothesized population proportion = 0.60
- X: & NBSP; Cư dân ủng hộ luật: 64residents who tư vấn law: 64
- N: & nbsp; cỡ mẫu = 100sample size = 100
Mã sau này đã cho toàn bộ chúng ta biết cách sử dụng hiệu suất cao tỷ lệ_ztest để thực thi một thử nghiệm Z mẫu:proportions_ztest function to perform a one sample z-test:
#import proportions_ztest function
from statsmodels.stats.proportion import proportions_ztest
#perform one proportion z-test
proportions_ztest(count=60, nobs=100, value=0.64)
(-0.8164965809277268, 0.41421617824252466)
Từ đầu ra, toàn bộ chúng ta hoàn toàn có thể thấy rằng thống kê thử nghiệm Z là -0.8165 và giá trị p. tương ứng là 0,4142. Vì giá trị này sẽ không còn nhỏ hơn α = 0,05, chúng tôi không từ chối giả thuyết null. Chúng tôi không còn đủ dẫn chứng để nói rằng tỷ suất dân cư ủng hộ luật khác với 0,60.-0.8165 and the corresponding p.-value is 0.4142. Since this value is not less than α = 0.05, we fail to reject the null hypothesis. We do not have sufficient evidence to say that the proportion of residents who tư vấn the law is different from 0.60.
Tài nguyên tương hỗ update
Giới thiệu về một máy tính kiểm tra z tỷ suất z tỷ suất
One Proportion Z-Test Calculator
How to Perform a One Proportion Z-Test in Excel
How to Perform a One
Proportion Z-Test in R
Trong nội dung bài viết này, chúng tôi sẽ xem xét cách tiếp cận để thực thi một thử nghiệm Z theo tỷ suất trong ngôn từ lập trình Python. & NBSP;
Test Z là một thử nghiệm thống kê để xác lập xem hai phương tiện đi lại dân số có rất khác nhau hay là không khi những phương sai được nghe biết và kích thước mẫu lớn. is a statistical test to determine whether two population means are different when the variances are known and the sample size is large.
Công thức thử nghiệm Z-Test một tỷ suất:
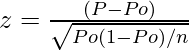
Where:
- P: Tỷ lệ mẫu được quan sát Observed sample proportion
- PO: Tỷ lệ dân số giả thuyếtHypothesized Population Proportion
- N: cỡ mẫu & nbsp;Sample size
Bài kiểm tra Z theo tỷ suất sử dụng những giả thuyết null sau:
- H0: P = P0 (Tỷ lệ dân số bằng với tỷ suất giả thuyết P0)
Giả thuyết thay thế hoàn toàn có thể là hai đuôi, đuôi trái hoặc đuôi phải:
- H1 (hai đuôi): P ≠ P0 (Tỷ lệ dân số hai đuôi không bằng một số trong những giá trị giả thuyết P0)
- H1 (đuôi trái): P
- H1 (đuôi phải): p.> p0 (tỷ suất dân số đuôi phải to nhiều hơn một số trong những giá trị giả thuyết P0)
Phương pháp 1: Tính toán & NBSP; Bài kiểm tra Z theo tỷ suất sử dụng Công thức
Trong phương pháp này, chúng tôi sẽ tính toán thử nghiệm Z theo tỷ suất bằng phương pháp sử dụng công thức đã cho và chỉ việc đặt giá trị đã cho vào công thức và nhận kết quả.
Formula:
z=(P-Po)/sqrt(Po(1-Po)/n
Trong ví dụ này, chúng tôi đang sử dụng giá trị P đến 0,86, PO đến 0,80 và N đến 100, và bằng phương pháp sử dụng điều này, chúng tôi sẽ tính toán một bài kiểm tra Z theo tỷ suất trong ngôn từ lập trình Python.
Python
import math
P = 0.86
Po =
z=(P-Po)/sqrt(Po(1-Po)/n1
z=(P-Po)/sqrt(Po(1-Po)/n2= z=(P-Po)/sqrt(Po(1-Po)/n4
z=(P-Po)/sqrt(Po(1-Po)/n5= z=(P-Po)/sqrt(Po(1-Po)/n7z=(P-Po)/sqrt(Po(1-Po)/n8z=(P-Po)/sqrt(Po(1-Po)/n9
1.49999999999999840____7 1.499999999999998421.499999999999998431.499999999999998441.49999999999999845z=(P-Po)/sqrt(Po(1-Po)/n8z=(P-Po)/sqrt(Po(1-Po)/n91.499999999999998481.49999999999999849
(-1.4999999999999984, 0.1336144025377165)0____7 (-1.4999999999999984, 0.1336144025377165)21.49999999999999848(-1.4999999999999984, 0.1336144025377165)4
(-1.4999999999999984, 0.1336144025377165)5(-1.4999999999999984, 0.1336144025377165)6
Output:
1.4999999999999984
Phương pháp 2: Tính toán & nbsp; Phân tích Z theo tỷ suất
Theo cách tiếp cận này, trước tiên toàn bộ chúng ta cần nhập thư viện StatSmodels.stats.prop-phần vào trình biên dịch Python và tiếp theo đó gọi hàm Tỷ lệ_ztest () để đơn thuần và giản dị hóa một thử nghiệm Z theo tỷ suất bằng phương pháp thêm những tham số vào hàm.
Chức năng tỷ lệ_ztest (): Hàm này được sử dụng để kiểm tra tỷ suất nhờ vào thử nghiệm (z) thông thường.This function is used to test for proportions based on the normal (z) test.
Cú pháp: Tỷ lệ_ztest (đếm, NOB, value = none, thay thế = hai mặt hai mặt) & nbsp;proportions_ztest(count, nobs, value=None, alternative=’two-sided’)
Parameters:
- Đếm: Số lượng thành công xuất sắc trong những thử nghiệm quý tộc. the number of successes in nobs trials.
- NOB: Số lượng thử nghiệm hoặc quan sát, với cùng chiều dài với số lượng. the number of trials or observations, with the same length as count.
- Giá trị: Tỷ lệ dân số giả thuyết.the hypothesized population proportion.
- Thay thế: Giả thuyết thay thế. & nbsp; The alternative hypothesis.
Trong ví dụ này, chúng tôi sẽ sử dụng những giá trị tương tự như được sử dụng trong ví dụ trước và bỏ qua những giá trị này theo hàm tỷ lệ_ztest (), chúng tôi sẽ tính toán thử nghiệm Z theo tỷ suất trong ngôn từ lập trình Python.
Python
(-1.4999999999999984, 0.1336144025377165)7 (-1.4999999999999984, 0.1336144025377165)8import import0
import1=import3import4=
z=(P-Po)/sqrt(Po(1-Po)/n4import7=0.86math0
Output:
(-1.4999999999999984, 0.1336144025377165)
Làm thế nào để bạn thực thi một tỷ suất z
Làm thế nào để thực thi một thử nghiệm Z tỷ suất trong Python.. H1 (hai đuôi): P ≠ P0 (tỷ suất dân số không bằng một số trong những giá trị giả thuyết P0). H1 (đuôi trái): p. H1 (đuôi phải): p.> p0 (tỷ suất dân số to nhiều hơn một số trong những giá trị giả thuyết P0).
Làm thế nào để bạn làm một tỷ suất z
Quy trình thực thi một bài kiểm tra giả thuyết tỷ suất Z mẫu.. Nêu giả thuyết null và giả thuyết thay thế .. Alpha trạng thái, nói cách khác xác lập mức ý nghĩa .. Tính toán thống kê kiểm tra .. Xác định giá trị tới hạn (từ bảng giá trị tới hạn). Xác định những tiêu chuẩn từ chối .. Cuối cùng, lý giải kết quả ..
Làm thế nào để bạn thực thi một bài kiểm tra tỷ suất trong Python?
Thư viện tỷ suất cho trình biên dịch Python và tiếp theo đó gọi hàm Tỷ lệ_ztest () để đơn thuần và giản dị hóa việc kiểm tra Z theo tỷ suất bằng phương pháp thêm những tham số vào hàm.Chức năng tỷ lệ_ztest (): Hàm này được sử dụng để kiểm tra tỷ suất nhờ vào thử nghiệm (z) thông thường.. proportions_ztest() function: This function is used to test for proportions based on the normal (z) test.
Bài kiểm tra tỷ suất 1 là gì?
Thử nghiệm tỷ suất 1 cho bạn biết liệu tỷ suất này còn có bằng giá trị tiềm năng hay là không.Để đặt nó trong những thuật ngữ thống kê rõ ràng hơn, quy trình này tính toán một khoảng chừng tin cậy và thực thi một bài kiểm tra giả thuyết.Giả thuyết khống của bạn là tỷ suất dân số (P) bằng với giá trị giả thuyết (H0: P = P0).tells you whether the proportion is equal to a target value. To put it in more starkly statistical terms, the procedure computes a confidence interval and performs a hypothesis test. Your null hypothesis is that the population proportion (p.) equals a hypothesized value (H0: p. = p0).Tải thêm tài liệu liên quan đến nội dung bài viết Hướng dẫn one proportion z test in python – kiểm tra một tỷ suất z trong python
programming
python
Statsmodels z-test




Share Link Tải Hướng dẫn one proportion z test in python – kiểm tra một tỷ suất z trong python miễn phí
Bạn vừa Read Post Với Một số hướng dẫn một cách rõ ràng hơn về Video Hướng dẫn one proportion z test in python – kiểm tra một tỷ suất z trong python tiên tiến và phát triển nhất và Chia SẻLink Tải Hướng dẫn one proportion z test in python – kiểm tra một tỷ suất z trong python miễn phí.

Thảo Luận vướng mắc về Hướng dẫn one proportion z test in python – kiểm tra một tỷ suất z trong python
Nếu sau khi đọc nội dung bài viết Hướng dẫn one proportion z test in python – kiểm tra một tỷ suất z trong python vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha
#Hướng #dẫn #proportion #test #python #kiểm #tra #một #tỷ #lệ #trong #python