Kinh Nghiệm về Tứ giác ABCD là hình bình hành cần thêm Đk gì về hai tuyến phố chéo để ABCD là hình thoi Mới Nhất
Pro đang tìm kiếm từ khóa Tứ giác ABCD là hình bình hành cần thêm Đk gì về hai tuyến phố chéo để ABCD là hình thoi được Update vào lúc : 2022-11-03 12:40:08 . Với phương châm chia sẻ Bí kíp Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc Post vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
–o0o–
Nội dung chính Show
- Để hình bình hành AEBF là hình chữ nhật khi :AB = EF (1)
- Để hình chữ nhật AEBF là hình vuông vắn khi : AB _|_ EF
- Các góc trái chiều bằng nhau.
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Hai đường chéo chia những góc ra hình thoi thành 2 góc bằng nhau (đường phân giác).
- Hình thoi có toàn bộ tính chất của hình bình hành.
- Tứ giác có bốn cạnh bằng nhau là hình thoi.
- Tứ giác có 2 đường chéo là đường phân giác của toàn bộ bốn góc là hình thoi.
- Tứ giác có 2 đường chéo là đường trung trực của nhau là hình thoi.
- Hình bình hành có hai cạnh bên bằng nhau là hình thoi.
- Hình bình hành có hai tuyến phố chéo vuông góc với nhau là hình thoi.
- Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
- AM = MB; CP = PD
- AQ = QD; BN = NC
- AB = CD; AD = BC
bài 1 : Cho tam giác ABC. Gọi D, E lần lượt là trung điểm của AB và BC.
a.Chứng minh tứ giác ADEC là hình thang
b.Trên tia đối của tia DE lấy điểm F sao cho DF = DE.Chứng minh tứ giác AEBF là hình bình hành.
c.Với Đk nào của tam giác ABC để AEBF là hình vuông vắn?.
Giải.
trong tam giác ABC ,ta có:
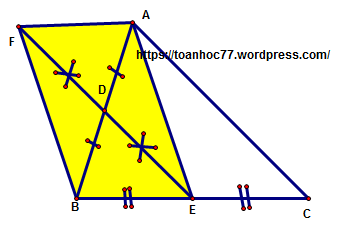
DA = DB (gt)
EB = EC (gt)
=>DE là đường trung bình tam giác ABC
nên DE//AC và DE=1/2AC
xét tứ giác DECA ta có:
DE//AC(cmt)
nên : DECA là hình thang
b.
Xét tứ giác AEBF, ta có :
AB cắt EF tại D
DA = DB (gt)
DE = DF (F là yếu tố đối xứng của E qua D)
= > AEBF là hình bình hành
c>.
Để hình bình hành AEBF là hình chữ nhật khi :AB = EF (1)
Mà : DE = AC/2 (cmt)
DE = EF/2 (F là yếu tố đối xứng của E qua D)
=> EF = AC (2)
Từ (1), (2) , suy ra : AB = AC
=> tam giác ABC cân tại A.
Để hình chữ nhật AEBF là hình vuông vắn khi : AB _|_ EF
Mà : EF // AC (cmt)
=> AB _|_ AC tại A.
=> tam giác ABC vuông cân tại A.
Vậy : Để AEBF là hình bình hành là hình vuông vắn thì tam giác ABC vuông cân tại A.
Bài 2 :
Cho tam giác ABC vuông ở C . Gọi M , N lần lượt là trung điểm của BC , AB . Gọi P là yếu tố đối xứng của M qua N .
a / Chứng minh :Tứ giác MBPA là hình bình hành.
b / Chứng minh : Tứ giác PACM là hình chữ nhật .
c / CN cắt PB ở Q. . Chứng minh BQ = 2 PQ
d / Tam giác ABC có thêm Đk gì thì hình chữ nhật PACM là hình vuông vắn .
Giải.
a)Xét tứ giác APBM,ta có:
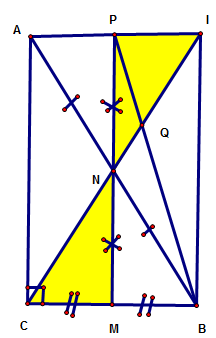
PN=NM(gt)
AN=NB(gt)
AB cắt MP tại N
=>APBM là hình bình hành(hai tuyến phố chéo AB và PM cắt nhau tại trung điểm N của mỗi đường)
b)ta có:
AMBP là hình bình hành(cmt)
nên AP=MB và AP//MB
mà CM=MB(gt)
nên AP=CM và AP//CM
xét tứ giác APMC ta có:
AP=CM và AP//CM
nên APMC là hình bình hành
ta lại sở hữu ^ACM=90^0(tam giác ABC là tam giác vuông tại C)
c)AP cắt CN tại I
Xét hai tam giác CMN và tam giác INP,ta có:
PN=NM(gt)
^CNM=^INP(đối đỉnh)
^MCN=^PIN(so le trong)
suy ra tam giác CMN=tam giác INP
nên CM=IP
mà:CM=AP(ACMP là hình chữ nhật)
=>IP=AP
xét tam giác AIB,ta có:
PA=PI(cmt)=>BP là đường trung tuyến thứ 1
NA=NB(gt)=>IN là đường trung tuyến thứ hai
mà:IN cắt BP tại Q.
=>Q. là trọng tâm
=>BQ=2PQ
d)để hình chữ nhật ACMP là hình vuông vắn khi:
AC=CM
mà CM=BC/2(M là trung điểm BC)
=>AC=BC/2 hay BC=2AC
vậy để hình chữ nhật ACMP là hình vuông vắn thì tam giác ABC có cạnh BC=2AC
Bài 3 :
Cho hình bình hành ABCD có M là trung điểm AB và N là trung điểm CD.
a/ Chứng minh : tứ giác AMND là hình bình hành.
b/ Chứng minh : tứ giác AMCN là hình bình hành.
c/ Chứng minh : AC, BD, MN đồng quy.
d/ Hình bình hành ABCD có điều kiện gì thì tứ giác AMND là hình chữ nhật, hình thoi, hình vuông.
Lý thuyết về hình thoi và cách chứng tỏ tứ giác là hình thoi học viên đã được tìm hiểu trong chương trình Toán 8, phân môn Hình học. Đây là một trong những phần kiến thức và kỹ năng trọng tâm của chương trình. Bài viết ngày hôm nay, THPT Sóc Trăng sẽ tổng hợp lại những kiến thức và kỹ năng cần ghi nhớ về hình thoi và cách chứng tỏ hình thoi nhanh nhất có thể.
I. LÝ THUYẾT VỀ HÌNH THOI
1. Định nghĩa Hình thoi
Bạn đang xem: Lý thuyết về hình thoi. Cách chứng tỏ tứ giác là hình thoi hay nhất

Hình thoi là tứ giác có bốn cạnh bằng nhau, là hình bình hành có 2 cạnh liền kề bằng nhau hoặc có đường chéo vuông góc với nhau.
Hình thoi là một hình bình hành đặc biệt quan trọng.
2. Tính chất Hình thoi
Hình thoi là hình có
3. Dấu hiệu nhận ra Hình thoi
Hình thoi là hình tứ giác đặc biệt quan trọng
Hình thoi là Hình bình hành đặc biệt quan trọng
Vì hình thoi là một dạng đặc biệt quan trọng của một hình bình hành nên nó sẽ có được khá đầy đủ tính chất của hình bình hành kèm thêm một số trong những tính chất khác ví như:
II. CÁC CÁCH CHỨNG MINH TỨ GIÁC LÀ HÌNH THOI CỰC HAY
Để chứng tỏ một tứ giác là hình thoi, những bạn hoàn toàn có thể vận dụng một trong những cách sau này. Cách nào thì cũng hay, tùy vào từng bài để vận dụng cách chứng tỏ nhanh nhất có thể nhé !

1. Cách 1: chứng tỏ tứ giác có 2 đường chéo là đường trung trực của nhau:
Ví dụ: Cho hình bình hành ABCD có AB = AC. Kéo dài trung tuyến AM của ΔABC và lấy ME = MA. Chứng minh tư giác ABEC là hình thoi.

Theo bài ra, ta có:
ΔABC cân tại A có trung tuyến AM
=> AM đồng thời là đường trung trực của BC
=> Tứ giác ABEC là hình thoi do có 2 đường chéo là đường trung trực của nhau. (đ.p..c.m)
2. Cách 2: chứng tỏ tứ giác có bốn cạnh bằng nhau
Ví dụ: Chứng minh rằng những trung điểm của bốn cạnh của một hình chữ nhật là những đỉnh của hình thoi.

Xét tam giác ABD có E và H lần lượt là trung điểm của AB và AD
=> EH là đường trung bình của tam giác
=> EH = 1/2 BD (1)
Chứng minh tương tự ta có: EF = 1/2 AC; FG = 1/2 BD; HG = 1/2 AC (2)
Vì ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2) và (3), ta suy ra EH = EF = HG = GF
=> Tứ giác EFGH là hình thoi do có bốn cạnh bằng nhau. (đ.p..c.m)
3. Cách 3: chứng tỏ tứ giác là hình bình hành có hai tuyến phố chéo vuông góc
Ví dụ: Gọi O là giao điểm hai tuyến phố chéo của hình bình hành ABCD. Chứng minh rằng giao điểm những đường phân giác trong của những tam giác AOB; BOC; COD và DOA là đỉnh của một hình thoi.

Gọi M, N, P, Q. lần lượt là giao điểm những phân giác trong của những tam giác AOB, BOC, COD và DOA.
Do O là giao điểm hai tuyến phố chéo AC và BD của hình bình hành ABCD nên OA = OC và OB = OD.
Xét ΔBMO và ΔDPO có:
Góc B1 = D1 và Góc O1 = O2 ( đối đỉnh ) và OB = OD (gt)
=> ΔBMO = ΔDPO (g. c. g)
=> OM = OP và những điểm M, O, P thẳng hàng (6)
Chứng minh tương tự: ON = OQ và N, O, P thẳng hàng (7)
Từ (6) và (7) Suy ra: Tứ giác MNPQ là hình bình hành do những đường chéo cắt nhau tại trung điểm mỗi đường. (8)
Mặt khác OM, ON là hai tuyến phố phân giác của hai góc kề bù nên OM ⊥ ON. (9)
Từ (8) và (9) suy ra: MNPQ là hình thoi do là hình bình hành có hai tuyến phố chéo vuông góc. (đ.p..c.m)
4. Cách 4: chứng tỏ tứ giác là hình bình hành có hai cạnh kề bằng nhau
Ví dụ: Cho tam giác ABC, lấy những điểm D, E theo thứ tự trên những cạnh AB, AC sao cho BD = CE. Gọi M, N, I, K lần lượt là trung điểm của BE, CD, DE, BC. Chứng minh rằng: IMNK là hình thoi.

Theo giả thiết ta có: M là trung điểm của BE và I là trung điểm của DE
=> MI là đường trung bình của ΔBDE
=> MI // BD và MI = 1/2 BD
Chứng minh tương tự, ta có:
NK // BD và NK= 1/2 BD
Do có MI // NK và MI = NK nên tứ giác MINK là hình bình hành (4)
Chứng minh tương tự, ta có: IN là đường trung bình của ΔCDE
=> IN = 1/2 CE mà CE = BD (gt) => IN = IM (5)
Từ (4) và (5) => Tứ giác MINK là hình thoi do là hình bình hành có hai cạnh kề bằng nhau. (đ.p..c.m)
III. BÀI TẬP CHỨNG MINH TỨ GIÁC LÀ HÌNH THOI
Bài 1: Cho hình bình hành ABCD có AC ⊥ CD. Gọi M, N lần lượt là trung điểm của AD và BC. Chứng minh rằng tứ giác AMCN là hình thoi.
Bài giải:
1.

Áp dụng định nghĩa và giả thiết vào hình bình hành ABCD ta được:
AB // CD
AC ⊥ CD
⇒AB⊥AC. Do đó ΔABC vuông ở A, ΔACD vuông ở C.
Do M, N là trung điểm của AD, BC theo giả thiết nên AN, CM thứ tự là trung tuyến ứng với cạnh huyền của hai tam giác vuông ABC và ACD
Do đó AN = 12BC; CM = 12AD
Mà AD = BC; AM = MD; BN = NC
⇒ AM = MC = CN = NA
Tứ giác AMCN có bốn cạnh bằng nhau nên là hình thoi.
Bài 2: Cho hình thoi ABCD. Trên hai cạnh BC, CD lần lượt lấy hai điểm M và N sao cho BM = DN. Gọi P, Q. thứ tự là giao điểm của AM và AN với đường chéo BD. Chứng minh rằng tứ giác APCQ là hình thoi.

Tứ giác APCQ là hình thoi.
Giải thích:
ΔABM = ΔADN (c.g.c)
⇒A1ˆ=A4ˆ, do đó A2ˆ=A3ˆ.
Gọi O là giao điểm của AC và BD thì AC ⊥ BD
ΔAPQ có đường cao AO là đường phân giác nên OP = OQ
Tứ giác APCQ có OP = OQ; OA = OC và AO là tia phân giác của PAQˆ nên tứ giác APCQ là hình thoi.
Bài 3: Cho ΔABC cân tại A, đường cao BD và CE. Gọi M là trung điểm của BC, H và K lần lượt là chân đường vuông góc kẻ từ M đến AB và AC, I là trung điểm của DE. Tứ giác MHIK là hình gì? Vì sao?

Xét ΔBDC và ΔCEB là 2 tam giác vuông có:
chung BC
DCBˆ=EBCˆ (ΔABC cân tại A)
⇒ ΔBDC = ΔCEB
⇒ EB = DC (1)
Dễ thấy ED // BC nên tứ giác DEBC là hình thang. (2)
Từ (1), (2) ta được tứ giác DEBC là hình thang cân.
Có: MK ⊥ AC; BD ⊥ AC nên MK // BD.
ΔBDC có M là trung điểm của BC; MK // BD nên MK là đường trung bình của ΔBDC
⇒ K là trung điểm của DC và MK = 12DB
Ta lần lượt chứng tỏ MH, HI, IK cũng là đường trung bình của những tam giác ΔBEC, ΔBED, ΔEDC
⇒ HM = 12EC; HI = 12BD; IK = 12EC.
Mà EC = BD (do DEBC là hình thang cân)
⇒ HI = IK = KM = MH
Vậy tứ giác HUKM là hình thoi.
Bài 4: Chứng minh rằng những trung điểm bốn cạnh của một hình chữ nhật là những đỉnh của một hình thoi.
Hướng dẫn:

Xét hình chữ nhật ABCD có M, N, P, Q. lần lượt là trung điểm của những cạnh AB, BC, CD, DA. Ta cần chứng tỏ tứ giác MNPQ là hình thoi
Vì ABCD là hình chữ nhật nên AAˆ=Bˆ=Cˆ=Dˆ=90∘ (1)
Áp dụng tính chất về cạnh và giả thiết vào hình chữ nhật ABCD ta được:
⇒ MA = MB = PC = PD và AQ = BN = CN = DQ (2)
Từ (1) và (2) suy ra bốn tam giác vuông MAQ, MBN, PCN, PDQ bằng nhau
⇒ MN = NP = PQ = QM
Tứ giác MNPQ có 4 cạnh bằng nhau nên là hình thoi.
Bài 5:Cho tam giác ABC vuông tại A có góc ABC = 60 độ. Kẻ tia Ax tuy nhiên tuy nhiên với BC, trên tia Ax lấy D sao cho AD = DC.a) Tính góc BAD và góc DAC.b) Chứng minh tứ giác ABCD là hình thang cân.
c) Gọi E là trung điểm của BC. Chứng minh tứ giác ADEB là hình thoi.
Vậy là những bạn vừa mới được tìm hiểu về chuyên đề hình thoi từ lý thuyết đến cách chứng tỏ một tứ giác là hình thoi hay nhất. Hi vọng, chia sẻ cùng nội dung bài viết, bạn nắm chắc hơn phần kiến thức và kỹ năng Hình học 8 vô cùng quan trọng này. Cách chứng tỏ hình vuông vắn cũng khá được THPT Sóc Trăng trình làng. Bạn tìm hiểu thêm nhé !
Đăng bởi: THPT Sóc Trăng
Chuyên mục: Giáo dục đào tạo và giảng dạy
Bản quyền nội dung bài viết thuộc trường THPT thành Phố Sóc Trăng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường THPT Sóc Trăng (thptsoctrang.edu.vn)
Tải thêm tài liệu liên quan đến nội dung bài viết Tứ giác ABCD là hình bình hành cần thêm Đk gì về hai tuyến phố chéo để ABCD là hình thoi




Share Link Download Tứ giác ABCD là hình bình hành cần thêm Đk gì về hai tuyến phố chéo để ABCD là hình thoi miễn phí
Bạn vừa tìm hiểu thêm tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Clip Tứ giác ABCD là hình bình hành cần thêm Đk gì về hai tuyến phố chéo để ABCD là hình thoi tiên tiến và phát triển nhất và Chia Sẻ Link Cập nhật Tứ giác ABCD là hình bình hành cần thêm Đk gì về hai tuyến phố chéo để ABCD là hình thoi miễn phí.

Thảo Luận vướng mắc về Tứ giác ABCD là hình bình hành cần thêm Đk gì về hai tuyến phố chéo để ABCD là hình thoi
Nếu sau khi đọc nội dung bài viết Tứ giác ABCD là hình bình hành cần thêm Đk gì về hai tuyến phố chéo để ABCD là hình thoi vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha
#Tứ #giác #ABCD #là #hình #bình #hành #cần #thêm #điều #kiện #gì #về #hai #đường #chéo #để #ABCD #là #hình #thoi