Thủ Thuật Hướng dẫn Hai đường thẳng tuy nhiên tuy nhiên là hai tuyến phố thẳng gì Chi Tiết
You đang tìm kiếm từ khóa Hai đường thẳng tuy nhiên tuy nhiên là hai tuyến phố thẳng gì được Cập Nhật vào lúc : 2022-04-18 18:30:05 . Với phương châm chia sẻ Bí kíp về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Admin lý giải và hướng dẫn lại nha.
Toán lớp 4 hai tuyến phố thẳng tuy nhiên tuy nhiên là một bài học kinh nghiệm tay nghề quan trọng giúp tăng trưởng tư duy hình học của trẻ.
Nội dung chính
- 1. Khái niệm hai tuyến phố thẳng tuy nhiên tuy nhiên
- 2. Hai hình ảnh tuy nhiên tuy nhiên trong thực tiễn
- 3. Bài tập thực hành thực tiễn toán lớp 4 hai tuyến phố thẳng tuy nhiên tuy nhiên
- 3.1. Bài tập
- 3.2. Đáp án
- Hai đường thẳng tuy nhiên tuy nhiên
- 2. Dấu hiệu nhận ra 2 đường thẳng tuy nhiên tuy nhiên
- 3. Tính chất hai tuyến phố thẳng tuy nhiên tuy nhiên
- 4. Cách vẽ hai tuyến phố thẳng tuy nhiên tuy nhiên
- 5. Chứng minh 2 đường thẳng tuy nhiên tuy nhiên
- 6. Bài tập Hai đường thẳng tuy nhiên tuy nhiên
- Quan hệ tương tự
- Đường thẳng tuy nhiên tuy nhiên với mặt phẳng
- 2 mặt phẳng tuy nhiên tuy nhiên
- trùng nhau
- cắt nhau tại tối thiểu một điểm nào đó
- tuy nhiên tuy nhiên với nhau
- phản xạ: một đường thẳng là tuy nhiên tuy nhiên với chính nó,
- đối xứng: Nếu một đường thẳng (d) tuy nhiên tuy nhiên với đường thẳng (d’) thì (d’) cũng tuy nhiên tuy nhiên với (d),
- bắc cầu: Nếu một đường thẳng (d) tuy nhiên tuy nhiên với đường thẳng (d’) và nếu (d’) tuy nhiên tuy nhiên với (d”) thì (d) cũng tuy nhiên tuy nhiên với (d”).
- cắt nhau tại tối thiểu một điểm xác lập nào đó
- tuy nhiên tuy nhiên: cắt nhau tại một điểm ở vô cực (có điểm chung ở vô cực)
- siêu tuy nhiên tuy nhiên: không bao giờ cắt nhau (không bao giờ có điểm chung)
- Hai góc so le trong bằng nhau
- Hai góc đồng vị bằng nhau
- Hai góc trong cùng phía bù nhau
- Hai góc ngoài cùng phía bù nhau
- Hai góc so le ngoài bằng nhau
- Vuông góc
- Định lý Thales
- Phan Đức Chính và đồng nghiệp, Sách giáo khoa Toán lớp 7 tập 1, Nhà xuất bản Giáo dục đào tạo và giảng dạy Việt Nam
- Trần Văn Hạo và đồng nghiệp, Sách giáo khoa Hình học 11, Nhà xuất bản Giáo dục đào tạo và giảng dạy Việt Nam
Ở bài học kinh nghiệm tay nghề trước, con đã hiểu được thế nào là hai tuyến phố thẳng vuông góc, trong bài học kinh nghiệm tay nghề ngày hôm nay, con sẽ tiếp tục học thêm một tính chất của những đường thẳng. Đó là toán lớp 4 hai tuyến phố thẳng tuy nhiên tuy nhiên.
1. Khái niệm hai tuyến phố thẳng tuy nhiên tuy nhiên

2. Hai hình ảnh tuy nhiên tuy nhiên trong thực tiễn

3. Bài tập thực hành thực tiễn toán lớp 4 hai tuyến phố thẳng tuy nhiên tuy nhiên
3.1. Bài tập
3.2. Đáp án
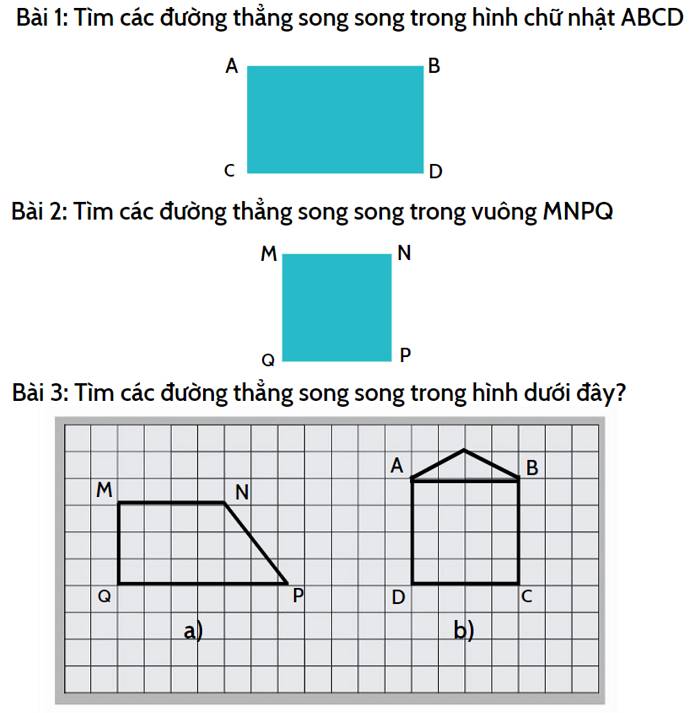
Bài 1:
Các đường thẳng tuy nhiên tuy nhiên trong hình chữ nhật ABCD là:
– AB và CD là hai tuyến phố thẳng tuy nhiên tuy nhiên
– AC và BD là hai tuyến phố thẳng tuy nhiên tuy nhiên
Bài 2:
Các đường thẳng tuy nhiên tuy nhiên trong vuông MNPQ là:
– MN và PQ là hai tuyến phố thẳng tuy nhiên tuy nhiên
– QM và NP là hai tuyến phố thẳng tuy nhiên tuy nhiên
Bài 3:
Các đường thẳng tuy nhiên tuy nhiên trong hình đã cho là:
a)
MN và PQ là hai tuyến phố thẳng tuy nhiên tuy nhiên
b)
– AB và CD là hai tuyến phố thẳng tuy nhiên tuy nhiên
– AD và BC là hai tuyến phố thẳng tuy nhiên tuy nhiên
Trên đấy là những kiến thức và kỹ năng cơ bản của bài học kinh nghiệm tay nghề toán lớp 4 hai tuyến phố thẳng tuy nhiên tuy nhiên, để ghi nhớ kiến thức và kỹ năng, đừng quên rèn luyện thêm nhé!
Giúp con nắm chắc công thức và những dạng toán khó phần Phân số, hình học… từ đó làm bài tập nhanh và đúng chuẩn. Mục tiêu điểm 10 môn Toán.
900.000₫
Chỉ còn 750.000 ₫
Chỉ còn 2 ngày
1 Khái niệm. Hai đường thẳng tuy nhiên tuy nhiên là hai tuyến phố thẳng không còn điểm chung kí hiệu là. Lý thuyết. Hai đường thẳng tuy nhiên tuy nhiên –
1 Khái niệm. Hai đường thẳng tuy nhiên tuy nhiên là hai tuyến phố thẳng không còn điểm chung kí hiệu là
1 Khái niệm.
– Hai đường thẳng tuy nhiên tuy nhiên là hai tuyến phố thẳng không còn điểm chung kí hiệu là
– Hai đường thẳng phân biệt thì cắt hoặc không cắt nhau như tuy nhiên tuy nhiên.
Quảng cáo
2. Dấu hiệu nhận ra hai tuyến phố thẳng tuy nhiên tuy nhiên.
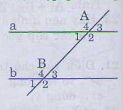
Nếu đường thẳng c cắt hai tuyến phố thẳng a,b và trong những góc tạo thành có một cặp góc sole trong bằng nhau(hoặc 1 cặp góc đồng vị bằng nhau ) thì a và b tuy nhiên tuy nhiên với nhau.
Chứng minh 2 đường thẳng tuy nhiên tuy nhiên
Hai đường thẳng tuy nhiên tuy nhiên là gì? Chứng minh 2 đường thẳng tuy nhiên tuy nhiên ra làm sao? Tính chất hai tuyến phố thẳng tuy nhiên tuy nhiên ra sao? Là vướng mắc được thật nhiều bạn học viên quan tâm.
2 đường thẳng tuy nhiên tuy nhiên là một chủ đề rất quan trọng trong chương trình toán học phổ thông những bạn sẽ tiến hành học từ lớp 6 đi học 11 và được ứng dụng thật nhiều trong thực tiễn. Trong nội dung bài viết ngày hôm nay Download.vn sẽ trình làng đến những bạn toàn bộ kiến thức và kỹ năng về Hai đường thẳng tuy nhiên tuy nhiên như tín hiệu, tính chất, cách chứng tỏ và một số trong những bài tập vận dụng. Thông qua tài liệu này những bạn có thêm nhiều gợi ý tìm hiểu thêm, trau dồi kiến thức và kỹ năng để nhanh gọn giải được những bài tập Toán.
Hai đường thẳng tuy nhiên tuy nhiên
Hai đường thẳng tuy nhiên tuy nhiên (trong mặt phẳng) là hai tuyến phố thẳng không còn điểm chung
2. Dấu hiệu nhận ra 2 đường thẳng tuy nhiên tuy nhiên
Dấu hiệu 1: Dựa vào khái niệm hai tuyến phố thẳng tuy nhiên tuy nhiên.
Dấu hiệu 2: Dựa vào một trong những đường thẳng cắt hai tuyến phố thẳng cần xét.
Nếu một đường thẳng c cắt hai tuyến phố thẳng a, b và trong những góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và b tuy nhiên tuy nhiên với nhau.
Dấu hiệu 3: Dựa vào quan hệ từ vuông góc đến tuy nhiên tuy nhiên
Cho đường thẳng a vuông góc với c, đường thẳng b vuông góc với c (a, b phân biệt) thì đường thẳng a tuy nhiên tuy nhiên với đường thẳng b (Hình vẽ trên)
Ta có công thức:
Dấu hiệu 4: Dựa vào tính cùng tuy nhiên tuy nhiên
Hai đường thẳng phân biệt cùng tuy nhiên tuy nhiên với đường thẳng thứ ba thì chúng tuy nhiên tuy nhiên với nhau
3. Tính chất hai tuyến phố thẳng tuy nhiên tuy nhiên
Nếu một đường thẳng cắt hai tuyến phố thẳng tuy nhiên tuy nhiên thì
– Hai góc so le trong bằng nhau
– Hai góc đồng vị bằng nhau
– Hai góc trong cùng phía bù nhau
Cho đường thẳng c cắt hai tuyến phố thẳng tuy nhiên tuy nhiên a và b như hình vẽ:
4. Cách vẽ hai tuyến phố thẳng tuy nhiên tuy nhiên
Vẽ đường thẳng CD trải qua điểm E và tuy nhiên tuy nhiên với đường thẳng AB cho trước.
Ta hoàn toàn có thể vẽ như sau:
Vẽ đường thẳng MN trải qua điểm E và vuông góc với đường thẳng AB.
Vẽ đường thẳng CD trải qua điểm E và vuông góc với đường thẳng MN ta được đường thẳng CD tuy nhiên tuy nhiên với đường thẳng AB
5. Chứng minh 2 đường thẳng tuy nhiên tuy nhiên
– Phương pháp 1: Tìm hai góc trong cùng phía bù nhau.
– Phương pháp 2: Tìm hai góc so le trong bằng nhau.
– Phương pháp 3: Tìm những góc đồng vị bằng nhau.
– Phương pháp 4: Áp dụng tiên đề Ơ-clít về đường thẳng tuy nhiên tuy nhiên: “Qua một điểm nằm ngoài đường thẳng chỉ có một đường thẳng tuy nhiên tuy nhiên với đường thẳng đó”.
– Phương pháp 5: Tìm ra hai tuyến phố thẳng phân biệt cùng vuông góc với đường thẳng thứ ba.
– Phương pháp 6: Tìm ra hai tuyến phố thẳng phân biệt cùng tuy nhiên tuy nhiên với đường thẳng thứ ba.
6. Bài tập Hai đường thẳng tuy nhiên tuy nhiên
Bài tập 1: Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của MA, lấy điểm D sao cho MA = MD. Chứng minh: AB // CD.
Bài tập 2: Cho tam giác ABC, M và N lần lượt là trung điểm của AB, AC. Trên tia đối của tia MC, lấy điểm D sao cho MD = MC. Trên tia đối của tia NB, lấy điểm E sao cho NE = NB. Chứng minh: DE // BC.
Bài tập 3: Cho tam giác cân ABC có AB = AC. Trên những cạnh AB và AC, lấy lần lượt điểm D và E sao cho AD = AE. Chứng minh: DE // BC.
Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. Mời bạn giúp hoàn thiện nội dung bài viết này bằng phương pháp tương hỗ update chú thích tới những nguồn uy tín. Các nội dung không còn nguồn hoàn toàn có thể bị nghi ngờ và xóa khỏi.
Trong hình học, sự tuy nhiên tuy nhiên là một đặc tính của những đường thẳng, mặt phẳng, hoặc tổng quát hơn là những không khí afin. Ban đầu, khái niệm tuy nhiên tuy nhiên do Euclide nêu lên trong tác phẩm Cơ sở (Euclid), cuốn sách về toán học và hình học nổi tiếng của ông. Theo thời hạn, khái niệm này đã quy đổi từ một định nghĩa mang tính chất chất tiên đề sang một định nghĩa hình học thông thường.

Đồ thị vẽ a và b là hai tuyến phố thẳng tuy nhiên tuy nhiên
Trong hình học Euclide, hai tuyến phố thẳng được gọi là tuy nhiên tuy nhiên khi chúng cùng nằm trên một mặt phẳng và không còn điểm chung. Trong trường hợp này, chúng được gọi là không cắt nhau, không giao nhau, hoặc không tiếp xúc nhau.
Hai đường thẳng bất kỳ trong hình học phẳng Euclide chỉ hoàn toàn có thể rơi vào 3 trường hợp:
Quan hệ tương tự
Nếu đồng ý những đường thẳng trùng nhau là tuy nhiên tuy nhiên với nhau, ta thấy quan hệ tuy nhiên tuy nhiên mang những tính chất sau:
Như vậy, ta kết luận: quan hệ tuy nhiên tuy nhiên là một quan hệ tương tự.
Mở rộng ra trên hình học phi Euclide, khái niệm đường thẳng được thay bằng khái niệm đường trắc địa. Hai đường trắc địa trong hình học phi Euclide chỉ hoàn toàn có thể rơi vào 3 trường hợp:
Ký hiệu để biểu thị sự tuy nhiên tuy nhiên là //. Ví dụ, nếu viết AB//CD, nghĩa là đường thẳng AB tuy nhiên tuy nhiên với đường thẳng CD.
Trong bộ mã Unicode, những hình tượng tuy nhiên tuy nhiên và không tuy nhiên tuy nhiên có code lần lượt là U+2225 (∥) và U+2226 (∦). Chúng được xếp vào phạm vi Mathematical Operators.
Qua 1 điểm nằm ngoài 1 đường thẳng, có duy nhất 1 đường thẳng tuy nhiên tuy nhiên với đương thẳng đã cho
Hai đường thẳng được gọi là tuy nhiên tuy nhiên khi có một đường thẳng thứ ba cắt hai tuyến phố thẳng trên và tạo với hai tuyến phố thẳng đó:
2 đường thẳng cùng vuông góc hoặc cùng tuy nhiên tuy nhiên với đường thẳng thứ 3 thì 2 đường thẳng đó tuy nhiên tuy nhiên với nhau
Nếu hai tuyến phố thẳng tuy nhiên tuy nhiên bị cắt bởi một đường thẳng thứ ba và có những cặp góc so le trong bằng nhau thì cặp góc so le trong còn sót lại cũng bằng nhau và những cặp góc so le ngoài cũng bằng nhau và những cặp góc đồng vị bằng nhau và những cặp trong cùng phía bù nhau và những cặp ngoài cùng phía bù nhau
Đường thẳng tuy nhiên tuy nhiên với mặt phẳng
Nếu một đường thẳng không nằm trong mặt phẳng và tuy nhiên tuy nhiên với một đường thẳng khác nằm trong mặt phẳng thì đường thẳng đó tuy nhiên tuy nhiên với mặt phẳng
Qua một đường thẳng tuy nhiên tuy nhiên với một mặt phẳng, giao tuyến của mặt phẳng đã cho với mọi mặt phẳng chứa đường thẳng đã cho sẽ tuy nhiên tuy nhiên với đường thẳng đó
Nếu đường thẳng tuy nhiên tuy nhiên với mặt phẳng thì đường thẳng này sẽ tuy nhiên tuy nhiên với tối thiểu một đường thẳng trong mặt phẳng.
Một đường thẳng tuy nhiên tuy nhiên với giao tuyến của 2 mặt phẳng thì đường thẳng đó tuy nhiên tuy nhiên với 2 mặt phẳng đã cho và ngược lại
Cho 2 đường thẳng chéo nhau, khi đó có duy nhất 1 mặt phẳng chứa đường thẳng này và tuy nhiên tuy nhiên với đường thẳng kia.
2 mặt phẳng tuy nhiên tuy nhiên
Nếu một mặt phẳng chứa 2 đường thẳng cắt nhau cùng tuy nhiên tuy nhiên với mặt phẳng kia thì 2 mặt phẳng đó tuy nhiên tuy nhiên với nhau.
Có duy nhất một mặt phẳng trải qua một điểm nằm ngoài mặt phẳng cho trước và tuy nhiên tuy nhiên với mặt phẳng đó
Qua một đường thẳng tuy nhiên tuy nhiên với một mặt phẳng, có duy nhất 1 mặt phẳng tuy nhiên tuy nhiên với mặt phẳng đã cho và chứa đường thẳng đó.
2 mặt phẳng phân biệt cùng tuy nhiên tuy nhiên với mặt phẳng thứ 3 thì 2 mặt phẳng đó tuy nhiên tuy nhiên với nhau.
Một mặt mẳng cắt 2 mặt phẳng tuy nhiên tuy nhiên thì tạo ra 2 giao tuyến tuy nhiên tuy nhiên
Một đường thẳng vuông góc với một trong 2 đường thẳng tuy nhiên tuy nhiên thì đường thẳng này cũng vuông góc với đường thẳng còn sót lại
Share Link Down Hai đường thẳng tuy nhiên tuy nhiên là hai tuyến phố thẳng gì miễn phí
Bạn vừa Read tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Review Hai đường thẳng tuy nhiên tuy nhiên là hai tuyến phố thẳng gì tiên tiến và phát triển nhất và Chia Sẻ Link Down Hai đường thẳng tuy nhiên tuy nhiên là hai tuyến phố thẳng gì miễn phí.

Giải đáp vướng mắc về Hai đường thẳng tuy nhiên tuy nhiên là hai tuyến phố thẳng gì
Nếu sau khi đọc nội dung bài viết Hai đường thẳng tuy nhiên tuy nhiên là hai tuyến phố thẳng gì vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha
#Hai #đường #thẳng #tuy nhiên #tuy nhiên #là #hai #đường #thẳng #gì