Thủ Thuật về Tứ giác nào nội tiếp đường tròn 2022
You đang tìm kiếm từ khóa Tứ giác nào nội tiếp đường tròn được Cập Nhật vào lúc : 2022-09-26 09:20:26 . Với phương châm chia sẻ Bí quyết về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Trong những hình sau. Bài 57 trang 89 sgk Toán lớp 9 tập 2 – Bài 7. Tứ giác nội tiếp
Nội dung chính
- Lý thuyết Tứ giác nội tiếp đường tròn
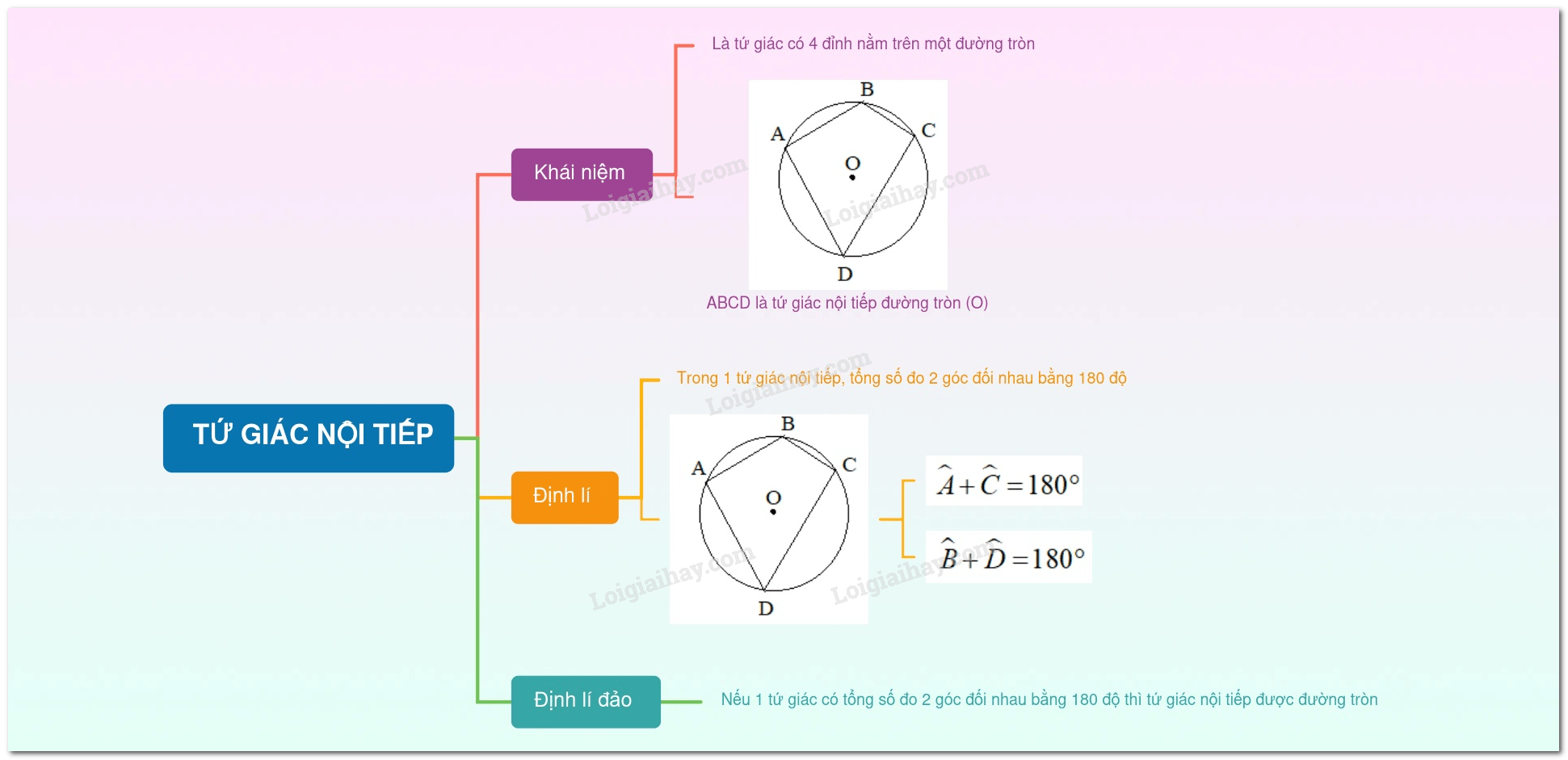
- 1. Khái niệm
- 2. Định lý
- Dấu hiệu nhận ra tứ giác nội tiếp
- Những cách chứng tỏ tứ giác nội tiếp đường tròn
- Bài tập minh họa
- Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó
- Chứng minh tứ giác có tổng 2 góc đối bằng 180°
- Chứng minh từ hai đỉnh
- Tứ giác có tổng số đo hai góc đối bằng nhau
- Chứng minh qua góc ngoài của tứ giác
- Chứng minh bằng phương pháp phản chứng
Bài 57. Trong những hình sau, hình nào nội tiếp được một đường tròn:
Hình bình hành, hình chữ nhật, hình vuông vắn, hình thang, hình thang vuông, hình thang cân ? Vì sao?
Hướng dẫn giải:
Hình bình hành nói chung không nội tiếp được đường tròn vì tổng hai góc trái chiều không bằng (180^0).Trường hợp riêng của hình bình hành là hình chữ nhật (hay hình vuông vắn) thì nội tiếp đường tròn vì tổng hai góc trái chiều là (90^0) + (90^0) = (180^0)
Quảng cáo
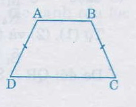
Hình thang nói chung, hình thang vuông không nội tiếp được đường tròn.
Hình thang cân (ABCD (BC= AD)) có hai góc ở mỗi đáy bằng nhau
(widehatA) = (widehatB), (widehatC) = (widehatD); mà (widehatA) +(widehatD) = (180^0) (hai góc trong cùng phía tạo bởi cát tuyến (AD) với (AD // CD)),suy ra (widehatA) +(widehatC) =(180^0). Vậy hình thang cân luôn có tổng hai góc trái chiều bằng (180^0)nên nội tiếp được đường tròn
1. Các kiến thức và kỹ năng cần nhớ
a. Định nghĩa tứ giác nội tiếp
Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên đường tròn đó.
Ví dụ: Trong Hình $1$ , tứ giác (ABCD) nội tiếp (left( O right)) và (left( O right)) ngoại tiếp tứ giác (ABCD.)
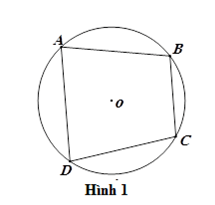
Định lý
– Trong một tứ giác nội tiếp, tổng số đo hai góc trái chiều bằng (180^circ ).
– Nếu một tứ giác có tổng số đo hai góc trái chiều bằng (180^circ ) thì tứ giác đó nội tiếp được đường tròn.
Ví dụ: Trong hình (1) , tứ giác nội tiếp(ABCD) có (widehat A + widehat C = 180^circ ;widehat B + widehat D = 180^circ ).
Một số tín hiệu nhận ra tứ giác nội tiếp
– Tứ giác có tổng hai góc đối bằng (180^circ ).
– Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh riêng với đỉnh đó.
– Tứ giác có bốn đỉnh cách đều một điểm (mà hoàn toàn có thể xác lập được). Điểm đó là tâm đường tròn ngoại tiếp tứ giác.
– Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn sót lại dưới cùng một góc (alpha ).
Chú ý : Trong những hình đã học thì hình chữ nhật, hình vuông vắn, hình thang cân nội tiếp được đường tròn.
2. Các dạng toán thường gặp
Dạng 1: Chứng minh tứ giác nội tiếp
Phương pháp:
Để chứng tỏ tứ giác nội tiếp, ta hoàn toàn có thể sử dụng một trong những phương pháp sau :
Cách 1. Chứng minh tứ giác có tổng hai góc đối bằng (180^circ ).
Cách 2. Chúng minh tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn sót lại dưới cùng một góc (alpha ).
Cách 3. Chứng minh tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh riêng với đỉnh đó.
Cách 4. Tìm được một điểm cách đều bốn đỉnh của tứ giác.
Dạng 2: Chứng minh những góc bằng nhau, đoạn thẳng bằng nhau, những đường thẳng tuy nhiên tuy nhiên, hệ thức Một trong những cạnh…
Phương pháp:
Sử dụng tính chất của tứ giác nội tiếp.
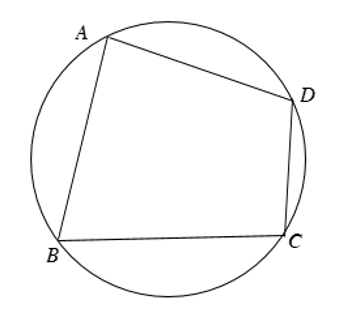
Tứ giác nội tiếp đường tròn là gì ? Những định lý, tính chất, dấu diệu nhận ra cũng như cách chứng tỏ tứ giác nội tiếp là gì ? Cùng chúng tôi tìm hiểu ngay dưới nội dung bài viết này nhé !
Tham khảo nội dung bài viết khác:
Lý thuyết Tứ giác nội tiếp đường tròn
1. Khái niệm
– Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn ( gọi tắt là tứ giác nội tiếp )
2. Định lý
+) Trong một tứ giác nội tiếp, tổng số đo hai góc trái chiều bằng 180°.
+) Nếu một tứ giác có tổng số đo hai góc trái chiều bằng 180° thì tứ giác đó nội tiếp được đường tròn.
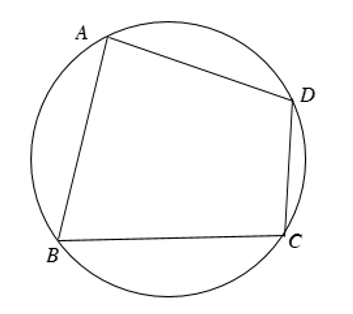
Tứ giác ABCD nội tiếp đường tròn (O), suy ra góc A + B + C + D = 180°
Dấu hiệu nhận ra tứ giác nội tiếp
+) Tứ giác có tổng hai góc đối bằng 180°.
+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh trái chiều.
+) Tứ giác có bốn đỉnh cách đều một điểm ( mà ta hoàn toàn có thể xác lập được ). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác đó.
+) Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn sót lại dưới một góc α.
Lưu ý: Để chứng tỏ một tứ giác là tứ giác nội tiếp ta hoàn toàn có thể chứng tỏ tứ giác đó là một trong những hình sau: Hình chữ nhật, hình vuông vắn, hình thang cân.
Những cách chứng tỏ tứ giác nội tiếp đường tròn
– Dưới đấy là 6 cách chứng tỏ tứ giác nội tiếp đường tròn:
Bài tập minh họa
Bài tập 1: Cho ΔABC nhọn, những đường cao AD, BE, CF cắt nhau tại H. Chứng minh rằng:
a) Tứ giác BCEF nội tiếp.
b) HA.HD = HB.HE = HC.HF
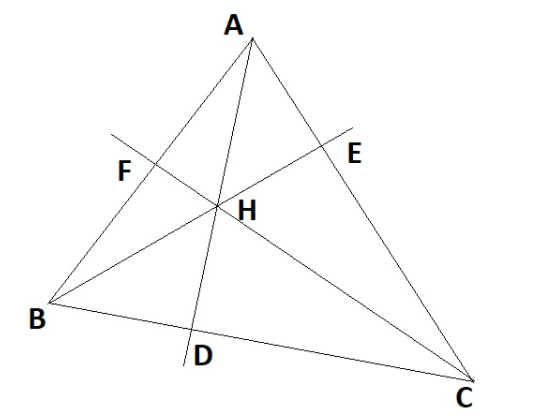
– Hướng dẫn giải:
a) Ta có ˆBEC = ˆBFC = 90°.
Suy ra tứ giác BCEF nội tiếp đường tròn có đường kính BC.
b) Gọi O là trung điểm của BC, vẽ đường tròn tâm O, đường kính BC. Xét ΔBHF và ΔCHE có:
ˆFHB = ˆEHC ( đối đỉnh ).
ˆEBF = ˆECF (hai góc nội tiếp cùng chắn).
Suy ra ΔBHF ∼ ΔCHE
BH/CH = HF/HE hay HB.HE = HC.HF (1).
Chứng minh tương tự riêng với ΔAHE và ΔBHD, ta có: HA.HD = HB.HE (2).
Từ (1) và (2) suy ra: HA.HD = HB.HE = HC.HF ( đpcm).
Với những nội dung trong bài, chúng tôi kỳ vọng sẽn mang đến những kiến thức và kỹ năng hữu ích nhất đến bạn !
Tải thêm tài liệu liên quan đến nội dung bài viết Tứ giác nào nội tiếp đường tròn




Chia Sẻ Link Cập nhật Tứ giác nào nội tiếp đường tròn miễn phí
Bạn vừa đọc Post Với Một số hướng dẫn một cách rõ ràng hơn về Video Tứ giác nào nội tiếp đường tròn tiên tiến và phát triển nhất và Share Link Cập nhật Tứ giác nào nội tiếp đường tròn Free.

Thảo Luận vướng mắc về Tứ giác nào nội tiếp đường tròn
Nếu sau khi đọc nội dung bài viết Tứ giác nào nội tiếp đường tròn vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha
#Tứ #giác #nào #nội #tiếp #đường #tròn