Thủ Thuật Hướng dẫn What is the maximum number of points in which 10 straight lines can intersect 5 circles 2022
Bạn đang tìm kiếm từ khóa What is the maximum number of points in which 10 straight lines can intersect 5 circles được Update vào lúc : 2022-11-03 07:40:09 . Với phương châm chia sẻ Bí quyết Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Admin lý giải và hướng dẫn lại nha.
Problem: 6 distinct chords are drawn in a circle. What is the maximum number of points they can intersect each other?
Nội dung chính Show
- What is the maximum number of points that intersect with 5 lines?
- What is the maximum number of points that 10 circles can intersect?
- What is the maximum number of points of intersection of 5 non overlapping circles A 10 B 15 C 20 D )= 25?
- What is the greatest number of points of intersection of 5 straight lines and four circles?
A chord is a line joining any two points on a circle.
To solve this problem, let’s start with just 2 chords. Any two straight lines can intersect each other in one point.
Now, if we draw a 3rd line, that can intersect the other two lines in most 2 points as shown below. Similarly, if we draw a 4th line, that can intersect the other 3 lines in most 3 points and so on.

So, the maximum number of points 3 lines can intersect each
other = 2 + 1
the maximum number of points 4 lines can intersect each other = 3 + 2 + 1
Do you see a pattern here?
So the maximum number of points 6 lines can intersect each other = 5 + 4 + 3 + 2 + 1
Using the sum of the series formula n(n+1) /2, we get 15.
In fact, we can generalize the above finding in a formula:
The maximum number of points n chords can intersect each other = 1 + 2 + 3 + … + (n -1) = n(n -1)/2
View Discussion
Improve Article
Save Article
View Discussion
Improve Article
Save Article
Given two integers X and Y, the task is to find the maximum number of points of intersection possible among
X circles and Y straight lines.
Example:
Input: X = 4, Y = 4
Output: 50
Explanation:
4 lines intersect each other 6 points and 4 circles intersect each other maximum of 12 points.
Each line intersects 4 circles 8 points.
Hence, 4 lines intersect four circles a maximum of 32 points.
Thus,
required number of intersections = 6 + 12 + 32 = 50.
Input: X = 3, Y = 4
Output: 36
Approach:
It can be observed that there are three types of intersections:
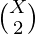 . Each such pair intersect most two points.
. Each such pair intersect most two points. . Each such pair intersect in most one point.
. Each such pair intersect in most one point.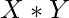 . Each such pair intersect in most two points.
. Each such pair intersect in most two points. So, the maximum number of point of intersection can be calculated as:
=>
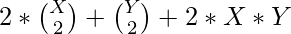
=> 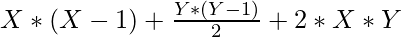
Thus, formula to find maximum number of point of intersection of X circles and Y straight lines is:
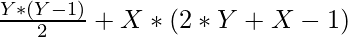
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int maxPointOfIntersection(int x, int y)
int k = y * (y – 1) / 2;
k = k + x * (2 * y + x – 1);
return k;
int main()
int x = 3;
int y = 4;
cout << (maxPointOfIntersection(x, y));
Java
class GFG
static int maxPointOfIntersection(int x, int y)
int k = y * (y – 1) / 2;
k = k + x * (2 * y + x – 1);
return k;
public static void main(String[] args)
int x = 3;
int y = 4;
System.out.print(maxPointOfIntersection(x, y));
Python3
def maxPointOfIntersection(x, y):
k = y * ( y – 1 ) // 2
k = k + x * ( 2 * y +
x – 1 )
return k
x = 3
y = 4
print(maxPointOfIntersection(x, y))
C#
using System;
class GFG
static int maxPointOfIntersection(int x, int y)
int k = y * (y – 1) / 2;
k = k + x * (2 * y + x – 1);
return k;
public static void Main(String[] args)
int x = 3;
int y = 4;
Console.Write(maxPointOfIntersection(x, y));
Javascript
<script>
function maxPointOfIntersection(x, y)
let k = y * (y – 1) / 2;
k = k + x * (2 * y + x – 1);
return k;
let x = 3;
let y = 4;
document.write(maxPointOfIntersection(x, y));
</script>
Time Complexity: O(1)
Auxiliary Space:
O(1)
What is the maximum number of points that intersect with 5 lines?
The maximum number of points of intersection when 5 lines are drawn in a plane, as shown, is 10 points. 6.
What is the maximum number of points that 10 circles can intersect?
Thus, the total possible number of intersection points of ten circles is 90.
What is the maximum number of points of intersection of 5 non overlapping circles A 10 B 15 C 20 D )= 25?
hence on solving we get 20 as our correct answer.
What is the greatest number of points of intersection of 5 straight lines and four circles?
Therefore, the maximum points of intersection of 5 lines and 4 circles are 62.
Tải thêm tài liệu liên quan đến nội dung bài viết What is the maximum number of points in which 10 straight lines can intersect 5 circles
Giới Tính
Trai




Share Link Tải What is the maximum number of points in which 10 straight lines can intersect 5 circles miễn phí
Bạn vừa tìm hiểu thêm tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Review What is the maximum number of points in which 10 straight lines can intersect 5 circles tiên tiến và phát triển nhất và Chia SẻLink Tải What is the maximum number of points in which 10 straight lines can intersect 5 circles miễn phí.

Thảo Luận vướng mắc về What is the maximum number of points in which 10 straight lines can intersect 5 circles
Nếu sau khi đọc nội dung bài viết What is the maximum number of points in which 10 straight lines can intersect 5 circles vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha
#maximum #number #points #straight #lines #intersect #circles